 ===================================================
===================================================Circuits are ``programs'' that are constructed from AND, OR, NOT operations and compute on the value set, {t,f}. We use equations to name the wires within the circuit, and we saw it was possible to deduce properties of the circuit even when we did not know the exact values of the circuit's inputs. This is critical for circuit design and analysis.
We can also make ``circuits'' from the operations, +, -, *, /, which compute on the value set of rational (fractional) numbers. That is, numbers travel along the wires. We use equations to name the numbers that travel in the circuits, and we apply the principles of algebra to deduce properties of the circuits we write.
In this chapter, we review principles of algebra and apply them to equationally defined systems (circuits).
Here are examples of assertions (facts) stated in algebra:
===================================================
5 > 2 + 1 (a)
x > 2 (b)
(2*x) - 1 = y (c)
x = y / 2 (d)
z > x + 1
===================================================
An assertion about a number can be stated directly, e.g., (a),
or the number can be given a name (a variable)
and we don't know its precise value, e.g., (b).
A property about a variable can be stated in terms of another one,
e.g., (c).
Sometimes, multiple assertions are made, e.g., (d).
Note that multiplication can be written without the star,
e.g., 2x is a shorthand for 2*x. We will use this abbreviation
from time to time.
Here are the main principles for deducing new facts from existing ones:
===================================================
5 > 2 + 1 simplifies to 5 > 3
2x = y + 1 simplifies to x = (y + 1) / 2,
because we divide both sides by 2, giving
2x / 2 = (y + 1) / 2,
and 2x / 2 simplifies to x.
(2*x) - 1 = y simplifies to 2x = y + 1
because we add 1 to both sides, giving
2x - 1 + 1 = y + 1, and we do arithmetic: -1 + 1 is 0.
===================================================
===================================================
Given
x = y / 2 and
z > x + 1
we substitute y / 2 for x in the second assertion, giving
z > (y / 2) + 1
Given
x = y / 3 and
2*z = x + 1
we substitute y / 3 for x into the second equation,
2z = (y / 3) + 1
We might simplify this equation to
2z = (y + 3) / 3
and then to
z = ((y + 3) / 3) / 2
and then to
z = (y + 3) / 6
===================================================
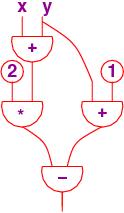
===================================================In the 1970's, this form of circuit, called a data-flow program, was used with computers with multiple processors for parallel computation of subexpressions. They are now again being investigated for use with multi-core processors.===================================================
Here is the equational system for the above circuit:
a = x + y
b = 2 * a
c = y + 1
d = b - c
Let's repeat the exercises at the end of the previous chapter for
this equational system.
First, say that x = 3 and y = 2; we can apply the simplification
laws to calculate the assertions that hold true after each equation
is ``executed'' within the program:
===================================================
premise: x = 3, y = 2
a = x + y
therefore, x = 3, y = 2, a = x + y
therefore, x = 3, y = 2, a = 5 (by substitution and simplification)
b = 2 * a
therefore, x = 3, y = 2, a = 5, b = 10
c = y + 1
therefore, x = 3, y = 2, a = 5, b = 10, c = 3
d = b - c
therefore, x = 3, y = 2, a = 5, b = 10, c = 3, d = 7
===================================================
We applied algebra to calculate the numerical values
for all of a,b,c,d. Of course, this is exactly what a computer does
when it computes and saves the values of the variables in storage cells.
Next, say that we know nothing
about the values of ``inputs'' x and y, and we want to know
about d's ``output'' value in terms of just x and y. This is the
bread-and-butter use of algebra, and it looks like this:
===================================================
a = x + y
therefore, a = x + y
b = 2 * a
therefore, a = x + y, b = 2 * a
and b = 2 * (x + y) by substitution
c = y + 1
therefore, b = 2 * (x + y), c = y + 1
d = b - c
therefore, b = 2 * (x + y), c = y + 1, d = b - c
and d = (2 * (x + y)) - (y + 1) by substitution
and d = 2x + y - 1 by simplification
===================================================
Here, we deduced the ``output property'' of d in terms of the
``inputs'' x and y. Even though we do not know the specific values of
x and y, it must be the case that the relationship,
d = 2x + y - 1 holds true when all the equations are ``computed.''
This reasoning is similar to what we use when we write assignment
commands in a programming language.
Let's do one more exercise. Say we have this equation set/circuit/program:
a = x - y
b = 2 * a
c = b + 1
Pretend that the algebra equations define a real-time controller and x and y are sensor inputs. Assume that the input value supplied by the x sensor will always be larger than the value supplied by the y sensor, that is, x > y must hold true. Assume also that x > 0. Say that we want to validate, to prove, that the value of the output, c, is greater than zero, that is, c > 0.
We can construct this proof by analyzing the equations with
algebra. Along the way, we will prove that all of a, b, and
c are greater than zero:
===================================================
premises: x > y, x > 0
a = x - y
since x > y, then x - y > y - y then x - y > 0 by simplification
since a = x - y, then a > 0 by substitution
b = 2 * a
since a > 0, then 2a > 0
then b > 0 by substitution
c = b + x
since b > 0 then b + x > 0 + x then b + x > x
since x > 0 then b + x > x > 0 then b + x > 0 by transitivity
then c > 0 by substitution
===================================================
So, we have proved that when the inputs satisfy the precondition
that x > y ^ x > 0, then the equations satisfy the
postcondition that c > 0.
These analyses were conducted before a computer executed the equations. Like an electronics engineer, who analyzes a circuit for voltage and resistance levels, we have analyzed the program and calculated in advance its behavioral properties.
Further, there is no self reference, that is, no equation, x = e, refers directly or indirectly to x within e. This is why the laws of algebra apply directly to the programs we have written so far.
If we violate either property, our analysis breaks down.
Consider this equation set:
y = x
x = x + 1
z = x
A naive application of algebra lets us deduce a falsehood:
===================================================
y = x
therefore, y = x
x = x + 1
therefore, y = x (?) and also x = x + 1 (impossible in algebra!)
z = x
therefore, z = x and y = x (??)
therefore, z = y (no way!)
===================================================
In particular, if x = x + 1 is a mathematical equality, then we can
subtract x from both sides of the equality and deduce 0 = 1.
It is very clear that the assignment command we use in programming is different from an algebraic equality: We must distinguish between the ``old'' value of x prior to the assignment, x = x + 1, that is needed to compute the expression, x + 1, and the ``new'' value of x that results from the equation's ``output.'' This complicates our algebra and leads us to programming logic.