Strings and tuples are examples of data structures, because they are ``structures'' that hold multiple pieces of ``data.'' (Strings hold multiple characters, and tuples hold whatever you want to insert into them!)
Strings and tuples are also called immutable structures,
because once you build one, you cannot alter its internal contents.
This is a subtle point, but it's worth some thought. Say you
construct this string:
"abcdefghijklm"
You might even name it:
mystring = "abcdefghijklm"
but you cannot change the internals of the string --- for example, you cannot replace the
d in the middle by, say, "X".
The best you can do is build a new string
from the one you started with and assign the new string to
the cell that held the original one:
mystring = mystring[:3] + "X" + mystring[4:]
You cannot do this assignment: mystring[3] = "X",
which is trying to replace character 3 in the string by a new character.
In a similar way, if we have a playing card:
mycard = ("hearts", "jack")
it makes no sense to alter the card after it is built:
mycard[1] = "ace" # this is not allowed on a tuple !
In this chapter, we learn about two forms of mutable data structure that will let you change their internal contents by assignment: a list and a dictionary.
Remember to read Dawson, Chapter 5.
But there are other structures that are based on the idea of ``permanent position'' or ``index number'' or ``address'' or ''key.'' When you use a spreadsheet program, you see a grid of cells in front of you. You can insert numbers or strings into the cells, but the cells can also be empty. Further, you can erase or replace the number you placed in the cell with another. The cells are not data, but they are ``permanent positions'' that you can fill with data. Each cell has a position --- an index --- in the spreadsheet.
Yet another example is a chessboard, which is an 8-by-8 grid of squares. You can place a chess piece on a square and you can move the piece off the square, leaving it empty. But the board always keeps its permanent positions of 64 squares.
A third example is a calendar, where each day of the month has its own square. You can insert appointments into a square, cancel appointments, or you can have a day without appointments. But the days are permanently positioned in the calendar, and each has its own index number.
There is a special data structure for modelling spreadsheets, game boards, and calendars. The structure has cells into which one can insert and update information. (This makes the structure mutable.) The usual name for this structure is array or matrix, but in Python, it is called a list.
(If you have used arrays in languages like Basic, C, or Java, you will soon see that Python lists are different because they can grow as needed. Some languages use the name, vector to describe an array that ``grows.'')
Here is an example:
I want to model my clothes chest in the computer. The chest has
a drawer for shirts, one for pants, and one for pairs of socks.
Here is a list that describes the shirts, pants, and socks I have
at the moment:
chest = ["3 shirts", "2 pants", "no socks"]
The chest holds 3 shirts, 2 pants, and no pairs of socks.
The list is written as a sequence, separated by commas
and surrounded by square brackets. (Remember that Python tuples are
surrounded by rounded brackets --- parentheses.)
Here is a drawing of the list in computer storage:

I can print my pants count by using the indexing operation:
print "I have", chest[1]
And I will see printed I have 3 pants.
A for-loop quickly prints my inventory:
for drawer in chest :
print drawer
This prints
3 shirts
2 pants
no socks
Or, I can merely say print chest. (Try it --- it prints
the list on one line, with its commas and brackets:
['3 shirts', '2 pants', 'no socks']
If I want to print the drawer number alongside its contents, I can
use this loop:
for index in range(len(chest)) :
print "drawer ", index, "holds", chest[index]
which prints
drawer 0 holds 3 shirts
drawer 1 holds 2 pants
drawer 2 holds no socks
The function, len(LIST), computes the number of cells in
its argument, LIST. (In the example,
len(chest) computes to 3.)
The function, range(N),
is a Python shortcut for generating the list (sequence),
[0, 1, 2, ..., N-1],
so that range(len(chest)) generates exactly the indexes
0, 1, 2, that we should use to index the cells in chest.
The use of range in for is not so elegant, but it makes
the Python for-loop behave like a Fortran- or C-style for-loop.
If I launder my socks and place them into the chest, I can update
my inventory with an assignment statement to the appropriate cell of the
list:
chest[2] = "3 pairs of socks"
This replaces "no socks" by "3 pairs of socks" in
cell 2 of the list. Such an assignment is impossible to do on
a tuple. (The reason is that tuples are stored differently inside
computer storage than are lists. Tuples are stored so that they can
be constructed and indexed fast. Lists are stored so that their
cells can be changed, but construction, indexing, and updating
are relatively slow.)
There is a method that makes a list grow by one cell to hold
a new value:
LIST.append(EXPRESSION).
For example,
say that we have
chest = ["3 shirts", "2 pants", "no socks"]
and we wish
to add a drawer for shorts:
chest.append("5 shorts")
print chest shows us:
["3 shirts", "2 pants", "no socks", "5 shorts"]
append is useful for building a list when
we do not know the correct size in advance. For example,
this loop builds a list to hold all the positive numbers
supplied by a user as input:
===============
number_list = [] # list starts empty
OK = True
while OK :
num = int(raw_input("Type a positive number (or a nonpositive, to quit): ")
if num > 0 :
number_list.append(num) # place num in a new cell in number_list
else :
OK = False
print number_list
================
Finally, we can store other items than strings and numbers into a
list. Here is an example, where each drawer of the chest holds
a ``label'' of the items saved in the drawer plus a count of the items:
chest = [ ["shirts", 3], ["pants", 2], ["socks", 0] ]
Each cell of chest holds a string, integer list.
I can print the inventory like this:
for drawer in chest:
print "I have", drawer[1], drawer[0]
This prints
I have 3 shirts
I have 2 pants
I have 0 socks
When I wash three pairs of socks, the inventory can be updated
like this:
chest[2][1] = chest[2][1] + 3
We make good use of such nested lists later in the chapter.
Perhaps you must
write a program that tallies the votes of a four-candidate election.
(For simplicity, we will say that the candidates' ``names''
are Candidate 0, Candidate 1, Candidate 2, and Candidate 3. )
Votes arrive one at a time,
where a vote for Candidate i is denoted by the number, i.
For example, two votes for Candidate 3 followed by one vote for Candidate
0 would appear:
Type your vote (0,1,2,3): 3
Type your vote (0,1,2,3): 3
Type your vote (0,1,2,3): 0
and so on.
Vote counting goes smoothly when we use a list that
holds the totals for the candidates:
votes = 4 * [0]
This makes a list of four cells, where each cell's value starts at zero.
Of course, votes[0] holds Candidate 0's votes, and so on.
When a vote arrives, it must be added to the appropriate element:
v = int(raw_input("Type your vote (0,1,2,3): ")
votes[v] = votes[v] + 1;
The algorithm for vote counting follows the ``input processing pattern'':
===================================================
processing = True
while processing
v = int(raw_input("Type your vote (0,1,2,3): ")
if v < 0 or v > 3 :
processing = False # bad vote, so quit
else :
votes[v] = votes[v] + 1
========================================================
Once all the votes are counted , they must be printed.
If we state
print votes # this prints the entire list, e.g., [25, 44, 12, 2]
If we state
for candidate in votes :
print candidate,
print
This prints the list's cells' contents on one line, like this:
25 44 12 2
To label the output in a useful way, we can use a while-loop:
count = 0
while count != len(votes) :
print "Candidate", count, "has", votes[count], "votes"
count = count + 1
Which would print
Candidate 0 has 25 votes
Candidate 1 has 44 votes
Candidate 2 has 12 votes
Candidate 3 has 2 votes
The same printout comes from this for-loop:
for count in range(len(votes))) :
print "Candidate", count, "has", vote[count], "votes"
Ensure that you understand all these different ways of printing
the vote totals.
Finally, what would happen if a person casts a vote for Candidate 5
(who does not exist)? The above program prevents such a vote,
because if we tried to perform,
votes[5] = votes[5] + 1
the program would stop with this error message:
Traceback (most recent call last): File "Since 5 is not an acceptable index to one of the cells in votes, there is an IndexError.", line 1, in ? IndexError: list index out of range
A calendar is just a spreadsheet where each cell is numbered
by a day of the month. Here is a series of examples.
First, to make a large list to represent the 28 days of February,
we say,
february = [ "" ] * 28
This makes a 28-celled list named february. (The * 28
``multiplies'' the one-celled list into a 28-celled one.)
print february
shows the list of 28 empty strings.
february[13] = "valentine's day"
inserts a message into cell 13 of the list.
(Remember that the indexes for the list start with 0, so cell number
13 is the fourteenth day in the list.)
We can print the calendar's contents, one week at a time, like this:
for count in range(len(february)) : # counts from 0 to 27
if count % 7 == 0 :
print # start a new week on a new line
print "February", count+1, ":", february[count], ". ",
The example can be improved if we make ``February 1''
print at the correct position for the day of the week when it falls.
(This is a good exercise to work.)
A chessboard's squares are cells, and we can use a numbering scheme
based on 0,1,2,... This works surprisingly well.
A chessboard has 64 squares:
ROW_SIZE = 8
BOARD_SIZE = ROW_SIZE * ROW_SIZE
board = [ () ] * BOARD_SIZE # place an empty tuple on each square
Chess pieces can be placed on the squares like this:
board[6] = ("white", "pawn")
If we wish to move the piece on square k to the right by one square,
we require
two assignments:
new_position = k + 1
board[new_position] = board[k]
board[k] = ()
If the second assignment is omitted, then the chess piece would
rest on both
squares simultaneously.
Say that we want to move a chess piece at square k
downwards one row; it's this simple:
new_position = k + ROW_SIZE
board[new_position] = board[k]
board[k] = ()
In both the previous examples, we should add if-commands that ensure
that the new_position does not extend ``off the board.''
This is left for you to do as an exercise.
A chessboard should be displayed as a square of
8 rows, each of which holds 8 squares.
We use this standard technique to print the list as a square:
ROW_SIZE = 8
for square in range(BOARD_SIZE) :
if count % ROW_SIZE == 0 : # print a newline at the end of each row
print
print square, # print the square's content, no newline
Later in this chapter we learn how to make and manipulate a true grid, which
is a list of 8 rows (cells), where each row (cell)
itself holds a
list of 8 squares:
# make the board:
board = [ ]
for row in range(ROW_SIZE) :
board.append([ () ] * ROW_SIZE)
board[5][5] = ("white", "pawn") # notice the _two_ indexes -- row 5, cell 5 !
# print the board, one row per line:
for row in board :
for square in row :
print square,
print
Say that a Python program contains this command: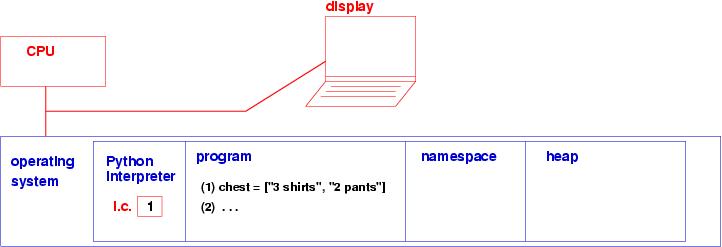
chest = ["3 shirts", "2 pants"]The command constructs the list of two strings in the heap, remembers the storage address where the list was made, and assigns that address to the variable in the namespace:
The diagram shows that the list was constructed at some address, say, addr1, in the heap, and addr1 is assigned to chest. Later, if the list's value is needed, as in,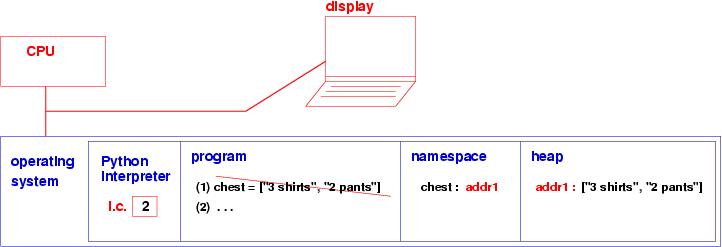
print chest[1]the expression, chest[1], is computed like this:
print chest[1] ==> print addr1[1] ==> print "2 pants"
Although the Python interpreter tries to hide from you the heap and the
addresses of lists, it is not completely successful.
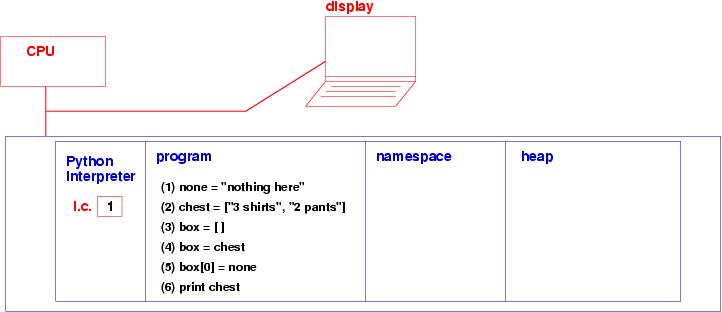
Here is an example:
none = "nothing here"
chest = ["3 shirts", "2 pants"]
box = []
box = chest # box holds the same address as chest !
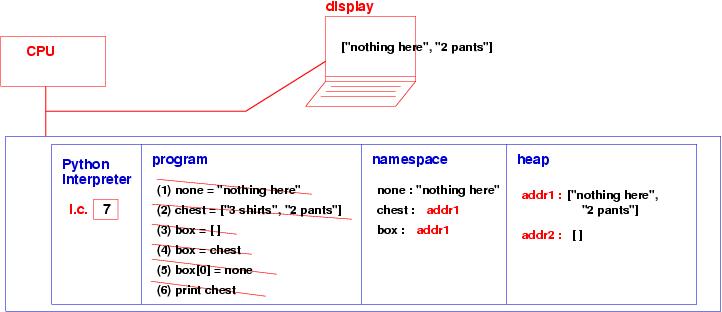
box[0] = none
print chest # prints ["nothing here", "2 pants"] !
As noted in the commentary, the assignment, box = chest,
places the address of chest's list into box's cell,
meaning that assignments to box's cells also affect chest's
cells. This is called aliasing.
We play out the example in steps: The beginning configuration
has an empty namespace and heap:
After the first three commands are
executed, we see that two lists are constructed in the heap and
their addresses are assigned to variables in the namespace:
The next assignment, box = chest assigns chest's
address to box:

and this means the assignment that follows updates the list at
addr1:

The update affects chest, as we see when the print command
executes:

The example suggests aliasing is bad, but this is too harsh of a statement.
It is true that aliasing can be confusing in examples like the
one above, but programs that build large databases of information
use aliasing as a trick to
link together data structures and reduce duplicate information.
For example, a database for the public library uses aliasing to ``link'' each patron to a list of books borrowed, and each borrowed book is linked to a list holding the book's bibliographic information. The links (aliases) eliminate duplicating information that would otherwise overwhelm the computer's storage. You will learn in a Data Structures course how to use aliasing in this smart way.
x = [1, 2, 3] x[1] = "a" print x
x = []
for cell in x
print cell
x = []
for i in range(4)
x.append(i)
print x
vec = [("shirts", 2)]
print vec[0]
vec[0][0] = 5
print vec[0]
vec = [1, 2, 3]
for cell in vec :
cell = 0
print vec
none = 0
items = ("shirts", "pants", "socks")
chest = [3, 2, none]
for index in range(len(chest)) :
print chest[index], items[index]
chest[2] = chest[2] + 3
new_item = "shorts"
items = items + (new_item,)
chest.append(5)
We now consider an example.
The techniques we saw in the clothes-chest example are useful for programs like spreadsheets, which collect, save, and display information. As a first project, let's study how a simple appointments calendar would be designed and built with lists.
Keeping it small, let's say that the calendar holds appointments
for exactly one afternoon of a day --- its user can make appointments
during the noon hour, and at the hours 1pm, 2pm, 3pm, and 4pm.
The behavior goes like this, where the user types information
in response to the prompts:
$ python Appointments.py
Type request: M(ake appt), V(iew appts), Q(uit): M
Type appt. time (hh:mm): 12:30
Type your appointment: lunch
Type request: M(ake appt), V(iew appts), Q(uit): M
Type appt. time (hh:mm): 2:00
Type your appointment: snack
Type request: M(ake appt), V(iew appts), Q(uit): 12:55
I don't understand your request; please try again.
Type request: M(ake appt), V(iew appts), Q(uit): m
Type appt. time (hh:mm): 12:55
Type your appointment: nap
Type request: M(ake appt), V(iew appts), Q(uit): V
Your appointments:
12:30: lunch
12:55: nap
2:00: snack
Type request: M(ake appt), V(iew appts), Q(uit): Q
The program that makes the calendar come to life holds appointments
for each of the 5 hours of the afternoon, and some
hours might have no appointments at all. This
suggests we use a list whose cells represent the
the 5 hours for appointments. Here is a sketch of the data structure:
The picture shows that each cell will hold zero or more appointments.
How might we save a sequence of appointments in a cell?
A tuple
of appointments is a good solution (but it is not the only one).

How is the list maintained? The answer is given by the algorithm
we write, which looks like the standard
``input-transaction processing'' pattern:
processing = True
while processing :
READ AN INPUT TRANSACTION;
if THE TRANSACTION INDICATES THAT THE LOOP SHOULD STOP :
processing = false
else :
PROCESS THE TRANSACTION
For the appointment manager, the PROCESS THE TRANSACTION
part will ask if the user wants to make a new appointment or
view the whole calendar. Here is the algorithm:
# start with an empty calendar for noon, 1pm, 2pm, 3pm, 4pm:
calendar = [(), (), (), (), ()]
processing = True
while processing :
read the request code ("M" or "V" or "Q")
if the request code == "Q" : # Quit
processing = False
elif code == "V" : # View all appointments
print all the appointments in the calendar
elif code == "M" : # Make a new appointment
read the time of the new appointment
read the appointment text
store the appointment into the calendar
Now, let's refine the "V" (print all the appointments in the calendar)
part --- it is a for-loop:
for hour in calendar :
... print all the appointments in the hour (*)
Since each hour (cell) of the calendar holds a tuple, we do line (*)
with another loop, which prints the contents of the tuple:
for hour in calendar :
for appointment in hour :
print appointment
Next, consider how we might make an appointment. First, we read
the time of the new appointment (e.g., "12:30") and the text
("lunch"). We concatenate these two strings together
and store the information into the tuple that lives at the cell for the
noon hour. The coding will look something like this:
# appt_time = ... READ "12:30"
# appt = ... READ "lunch"
# appt_hour = 0 # we somehow calculate this from the "12" in "12:30"!
new_appt = appt_time + ": " + appt
calendar[appt_hour] = calendar[appt_hour] + (new_appt,)
But the missing part is: how do we extract the appt_hour,
12, from the string, "12:30" ?
The answer uses a new Python trick, a method
named split:
# split the time in two, into its hours part and its minutes part:
hour_and_minutes = appt_time.split(":") # split is a string method
# get the hours part from the list, [hours, minutes]:
appt_hour = int(hour_and_minutes[0])
The new method, STRING.split(SEPARATOR_STRING),
examines STRING and ``splits'' it into a list
of those pieces that are separated by SEPARATOR_STRING.
For example,
appt_time = "12:30"
hour_and_minutes = appt_time.split(":")
print hour_and_minutes
prints the list, ["12", "30"].
The split method is a good trick to use when extracting
numbers (or individual words) from a string.
Figure 1 assembles the the program:
FIGURE 1==============================
# Appointments
# maintains a calendar of afternoon appoinments from noon up to 5pm.
# assumed input: a series of requests of these three forms:
# (i) M (for ''Make a new appointment'')
# followed by the time, typed in the format, hh:mm
# followed by the appointment, typed on a single line
# (ii) V (for ''View all appointments)
# (iii) Q (for ``Quit'')
# guaranteed output: when V is typed, a listing of all appointments is printed
# start with an empty calendar for noon, 1pm, 2pm, 3pm, 4pm:
calendar = [(), (), (), (), ()]
more_requests = True
while more_requests :
request = raw_input("\nType request: M(ake appt), V(iew appts), Q(uit): ")
code = request[0].upper()
if code == "Q" : # Quit
more_requests = False
elif code == "V" : # View all appointments
print "Your appointments: "
for hour in calendar :
for appointment in hour :
print appointment
elif code == "M" : # Make a new appointment
# read the time of the appointment:
appt_time = raw_input("Type appt. time (hh:mm): ")
# split the time in two, into its hours part and its minutes part:
hour_and_minutes = appt_time.split(":") # split is a string method
# get the hours part from the list, [hours, minutes]:
appt_hour = int(hour_and_minutes[0])
# read the appointment:
appt = raw_input("Type your appointment: ")
# save it in the calendar; first, treat noon hour (12) as 0 hour:
if appt_hour == 12 :
appt_hour = 0
new_appt = appt_time + ": " + appt
calendar[appt_hour] = calendar[appt_hour] + (new_appt,)
else :
print "I don't understand your request; please try again."
print "Have a nice day."
raw_input("\n\npress Enter to finish")
ENDFIGURE=============================================
Here is what the data structure looks like after the example
appointments have been added to it:
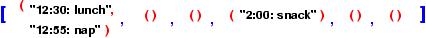
Now we should test the program with the behavior seen earlier and try other behaviors, too.
Type request: M(ake appt), V(iew appts), H(our to view), Q(uit): H Type appt. hour: 12 Your appointments: 12:30: lunch 12:55: nap
Consider a library's card catalog. Each library book must be entered into the card catalog, where the book is uniquely identified by its key --- its catalog number. Such catalog numbers are typically a mix of letters and numbers and punctuation, e.g., QA79.03. There is no simple way of using integer codes like 0, 1, 2, ... to stand for the catalog numbers.
Another example is a telephone book, where a person's name is used
as the key for finding the person's telephone number:
Yet
another example
is a numerical phone book, where the telephone number is used as the
key for finding the name of the number's owner.

Indeed, just about
every real-life database uses keys to organize and find
information.

A data structure that holds elements each of which has a unique key, is called a dictionary. (The name comes from real-life dictionaries, which are collections of definitions whose keys are words.) Python is one of the few languages that has a dictionary data structure ready for you to use.
(Other languages, like C and Pascal, have a simpler version of dictionary, called a record structure or struct. You will soon see that, unlike record structures, Python dictionaries can grow as needed and the set of allowable keys/fieldnames is not fixed in advance.)
tel_book = {"Jane Sprat": 4098, "Jake Jones": 4139, "Lana Lang": 2135}
To look up Lana Lang's phone number, we use her name as the index (key):
print tel_book["Lana Lang"]This prints 2135. But it is an error if we look up a key that is not in the dictionary. For this reason we should first is the key is present, e.g.,
if "Mary Hartman" in tel_book :
print tel_book["Mary Hartman"]
If Lana Lang receives a new phone number,
say, 9999, we can update the dictionary:
tel_book["Lana Lang"] = 9999
We can print the contents of the telephone book this simply:
print tel_book
For the above example, we see that the entries are not
printed alphabetically by key, but like this:
{'Jake Jones': 4139, 'Lana Lang': 9999, 'Jane Sprat': 4098}
The reason for the ``mixed up'' printout is
because the dictionary is stored within the computer as
a structure called a hash table (which
we will not study here --- you will learn about it in your Data Structures
course).
If a new person is added to the telephone book, we can update the
dictionary with an assignment, e.g.,
tel_book["Mary Hartman"] = 6744
but it is illegal to try to add a new person with the same name (key)
as someone already in the dictionary --- every element must have a
distinct key.
We can easily delete an entry from a dictionary, e.g.,
moved_away = "Jake Jones"
if moved_away in tel_book :
del tel_book[moved_away]
We use a for-loop to systematically examine all the
keys in a dictionary and so process all
the dictionary's elements:
for k in tel_book :
print k, tel_book[k]
(The loop looks at the keys, one by one, held in the dictionary.)
Finally, to print the dictionary's contents, ordered by its
keys, you can use two new Python methods, keys and sort:
keylist = tel_book.keys() # builds a list of all the keys used in tel_book
keylist.sort() # sorts (reorders) the list alphabetically
for k in keylist :
print k, ":", tel_book[k]
Of course, a dictionary can store arbitrary values with its keys.
Here is a modified phone book, which keeps addresses and phone numbers:
tel_book = {"Jane Sprat": ("200 First St.", 4098),
"Jake Jones": ("County Jail", 4139),
"Lana Lang": ("Smallville", 2135) }
A dictionary's keys are usually strings, but we can also
use integers. Here is the clothes-chest example, which started this
chapter, expressed as a dictionary with integer keys:
chest = {0: "3 shirts", 1: "2 pants", 2: "no socks"}
Here is yet another modelling of the chest, where the
drawers are named by the items they hold:
chest = {"shirts": 3, "pants": 2, "socks": 0}
Indeed, any immutable value (strings, numbers, booleans, even tuples)
can be used as a key to a dictionary. The keys can be mixed, as can
be the values:
places_Ive_been_in_my_town = { "101 Elm St." : "my house",
("3rd", "Vine") : "burger king",
100 : ["mall", "food court"] }
The appointments-manager program we built earlier in this chapter used a list, where the list's cells represented the hours of the day; appointments were saved within tuples. If we reconsider the program, we realize that each appointment has a ``key'' --- the time of the appointment.
Recall the behavior of the appointments manager:
Its user types the time and purpose of each appointment:
Type request: M(ake appt), V(iew appts), Q(uit): M
Type appt. time (hh:mm): 12:30
Type your appointment: lunch
Type request: M(ake appt), V(iew appts), Q(uit): M
Type appt. time (hh:mm): 2:00
Type your appointment: snack
Type request: M(ake appt), V(iew appts), Q(uit): m
Type appt. time (hh:mm): 12:55
Type your appointment: nap
Type request: M(ake appt), V(iew appts), Q(uit): V
Your appointments:
12:30: lunch
12:55: nap
2:00: snack
An appointment can be viewed as
a ``record'' whose ``key'' is the time of the appointment.
Here is a drawing of the appointments organized as a dictionary:
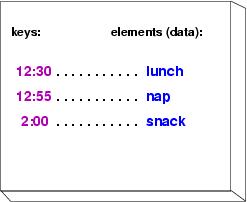
We can reuse most of the algorithm we designed for the appointment
manager. Indeed, the replacement of the list by the dictionary
makes the
program shorter and
simpler because we use an appointment's time as its key for insertion:
FIGURE=============================================
# Appointments
# maintains a calendar of appoinments from noon to 11:59pm
# the calendar begins as empty record
calendar = {}
more_requests = True
while more_requests :
request = raw_input("Type request: M(ake appt), V(iew appts), Q(uit): ")
code = request[0].upper()
if code == "Q" : # Quit
more_requests = False
elif code == "V" : # View all appointments
print "Your appointments: "
# print all appointments:
for time in calendar : # examine all keys
print time, calendar[time]
elif code == "M" : # Make a new appointment
# get the time of the appointment:
appt_time = raw_input("Type appt. time (hh:mm): ")
# get the appointment:
appt = raw_input("Type your appointment: ")
# save it in the calendar:
calendar[appt_time] = appt
else :
print "I don't understand your request; please try again."
print calendar # print the whole thing
raw_input("\nHave a nice day.")
ENDFIGURE======================================
Since dictionaries are mutable data structures, they are stored
in the heap, like lists. A dictionary is a collection of
KEY: ELEMENT pairs, and the pairs are not saved in any certain order.
Here is how we will display dictionaries in the heap:

To understand this, think about how we draw
a spreadsheet or a game board:
it is grid that looks like this:
(The numberings will be explained in a moment.)
We insert data (numbers or words or chess pieces) into the grid's cells.
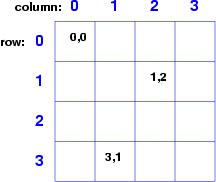
What is important here is the numbering --- rather than think about cell ``number 7'' or cell ``number 14,'' we think about the cell in ``row 1, column 2'' or ``row 3, column 1'' --- there are two dimensions to the structure we design.
In Python we build such a structure with a list of lists:
[["00", "01", "02", "03"], ["10", "11", "12", "13"], ["20", "21", "22", "23"], ["30", "31", "32", "33"]]
To see this more clearly, let's arrange the nested list into its ``rows'':
[ ["00", "01", "02", "03"],
["10", "11", "12", "13"],
["20", "21", "22", "23"],
["30", "31", "32", "33"] ]
This form of nested list is often called a matrix or
two-dimensional array. The numbering used in the example matrix
just seen is not an accident: If we write
grid = [ ["00", "01", "02", "03"],
["10", "11", "12", "13"],
["20", "21", "22", "23"],
["30", "31", "32", "33"] ]
and then say
print grid[1]
we would see
['10', '11', '12', '13']
which corresponds to ``row 1'' of the matrix.
If we wish to fetch and print the string "21" in grid,
we would say
print grid[2][1]
which names the string in ``row 2'', ``column 1'' in grid.
Here are some other exercises that you should try:
# print the grid in four lines, one row per line:
for row in grid :
print row
# print all the strings in the grid, listed one row per line on the display:
for row in grid :
for cell in row :
print cell,
print # start a new line
# print each string on its own line, labelled with its row-column position:
size = len(grid) # how many rows are in the grid
for i in range(size) :
for j in range(size) : # we are assuming that the grid is _square_
print "row", i, "column", j, ": ", grid[i][j]
# build a square matrix, the size given by the user, filled with strings
# that show the cell numbers, like in the above example:
size = int(raw_input("Type a grid size (a nonnegative int): "))
grid = []
if size > 0 :
for i in range(size) :
new_row = []
for j in range(size) :
value = str(i) + str(j)
new_row.append(value)
grid.append(new_row)
# place "XX"s across the diagonal of grid:
for i in range(size) :
grid[i][i] = "XX"
Grids are best used when you model cells whose addresses are based on two index numbers. A good example is a calendar for an entire year, where each day of the year is indexed by two coordinates --- the month and day. Another example is the layout of a multi-story hotel, where each room is indexed by its floor number and its room number. Gameboards, where the squares are identified by row, column numbers, are another example where grids might be used.
Type request: M(ake appt), V(iew appts), Q(uit): M Type appt. time (hh:mm): 2:00 Type your appointment: snackis a request to file the appointment, "snack" at the two coordinates, 2 (for the row), 00 (for the column). This means the calendar is modelled as a huge grid (nested list) with 5 rows, each row containing 60 elements (one for each minute of the hour).
The grid is created like this:
HOURS = 5 # for noon, 1pm, 2pm, 3pm, 4pm
MINUTES = 60 # in each hour
# build the nested list:
calendar = [] # will hold all the appointments
for i in range(HOURS) : # count from 0 to 4
calendar.append(MINUTES * [""]) # add one hour (row) of cells to calendar
If you print calendar, you will see 300 cells, each containing
an empty string.
When we make a new appointment, we split the appointment time
into its row, column, coordinates and place the appointment
in the selected cell (provided the cell isn't already filled
with a previous appointment):
appt_time = raw_input("Type appt. time (hh:mm): ")
hour_and_minutes = appt_time.split(":") # split the time in two
hour = int(hour_and_minutes[0]) # get the hours and minutes:
minute = int(hour_and_minutes[1])
# read the appointment:
appt = raw_input("Type your appointment: ")
if hour == 12 : # convert noon hour into hour = 0 :
hour = 0
if calendar[hour][minute] != "" : # is the cell already filled ?
print "error: you already have an appointment at that time"
else :
calendar[hour][minute] = appt
Here is the completed program:
FIGURE====================================================
import string
HOURS = 5 # model noon, 1pm, 2pm, 3pm, 4pm
MINUTES = 60
# build the nested list:
calendar = [] # will hold all appointments
for i in range(HOURS) : # count from 0 to 4
calendar.append( 60 * [""]) # add one hour of cells to the calendar
more_requests = True
while more_requests :
request = raw_input("\nType request: M(ake appt), V(iew appts), Q(uit): ")
code = request[0].upper()
if code == "Q" : # Quit
more_requests = False
elif code == "V" : # View all appointments
print "Your appointments: "
for hour in range(HOURS):
for minute in range(MINUTES):
appt = calendar[hour][minute]
if appt != "" :
if hour == 0 :
print "12:" + string.zfill(minute,2) + ":", appt
else :
print str(hour) + ":" + string.zfill(minute,2) + ":", appt
elif code == "M" : # Make a new appointment
appt_time = raw_input("Type appt. time (hh:mm): ")
hour_and_minutes = appt_time.split(":") # split the time in two
hour = int(hour_and_minutes[0]) # get the hours and minutes:
minute = int(hour_and_minutes[1])
appt = raw_input("Type your appointment: ")
if hour == 12 : # convert noon hour into hour = 0 :
hour = 0
if calendar[hour][minute] != "" : # is the cell already filled ?
print "error: you already have an appointment at that time"
else :
calendar[hour][minute] = appt
else :
print "I don't understand your request; please try again."
raw_input("\n\npress Enter to finish")
ENDFIGURE======================================================
Notice that it takes some work to properly print the hours, minutes
time from the row, column coordinates when all the appointments are
printed. (See the use of import string and
string.zfill(...).)
Modelling the calendar has a grid has a huge disadvantage: almost all of the cells of the calendar will remain empty. Perhaps it is not a tragedy to waste 300 cells in our small example, but this form of model would be unacceptable for a monthly calendar.
Perhaps the objective is to rearrange the numbers that label the pieces so that the numbers appear in ascending order. It will take some work, but you have time to kill, so you start, say, by sliding piece 1 into the empty space:
Now, you may move either piece 5, 2 (or 1 again); perhaps you move 5: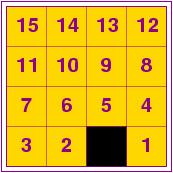
You continue playing with the puzzle for as long as you like.
Let's build a computerized slide puzzle, which has the same behavior as the physical one shown above. To build the program, we must select a data structure to represent the slide puzzle inside the computer. Since the puzzle board has cells and a cell might be empty, this suggests some form of list.
The obvious choice is a grid of integers, like
this
where the integer 0 represents the empty space. It is easy to
write the Python data structure:
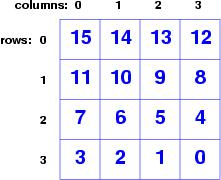
puzzle = [ [15, 14, 13, 12],
[11, 10, 9, 8],
[ 7, 6, 5, 4],
[ 3, 2, 1, 0] ]
But a second choice is a simple list, like this:
puzzle = [15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
Which representation is better? The answer depends --- assuming the human does not use the row-column coordinate numbers of the squares to slide pieces (instead, she would type the number on the piece itself), a two-coordinate indexing system is not essential to the game. This means either form of data structure will do.
So, we will construct the solution both ways and compare the results.
while True :
print the puzzle
ask the human for the number on the piece to move
try to move the piece (*)
Let's focus on the third step (*) in the loop: moving the selected
piece, say, the piece labeled by number num.
We must
find where piece num is situated in the puzzle
once found, verify that it is located adjacent to the empty space (number 0)
swap num and 0 in the puzzle
To refine these steps further, we must fix our choice of data structure
for the puzzle. We study the grid first and the list second.
puzzle = [ [15, 14, 13, 12],
[11, 10, 9, 8],
[ 7, 6, 5, 4],
[ 3, 2, 1, 0] ]
then
the difficult steps in the solution are indeed to
find where piece num is situated in the puzzle
once found, verify that it is located adjacent to the empty space (0)
swap num and 0 in the puzzle
To locate the piece the human wishes to move,
we search
the puzzle, examining all its integers, until we find num.
To search a grid, we use
a loop inside a loop, like this:
PUZZLE_SIZE = 4 # it's a 4-by-4 puzzle
# search the puzzle for the piece numbered num:
for i in range(PUZZLE_SIZE): # counts 0, 1, 2, 3.
for j in range(PUZZLE_SIZE) :
if num == puzzle[i][j] :
... remember i and j ...
Once we find num at position i, j, we must
verify that i, j are adjacent to the coordinates of the
empty space:
# Say that we wish to move the piece at coordinates (i,j) into the empty_space,
# and empty_space = (row, column) is the location of the empty space.
# Check if the empty_space is adjacent to i,j :
if (empty_space == (i-1, j)) \
or (empty_space == (i+1, j)) \
or (empty_space == (i, j-1)) \
or (empty_space == (i, j+1)) :
# if True,
... swap num and 0 in the puzzle ...
else : # False
print "illegal move --- try again"
Here is the completed coding:
FIGURE===============================================
# SlidePuzzle
# implements a slide-puzzle game.
# assumed input: a series of integers between 1 and 15, which indicate the
# pieces to move in the slide puzzle
# guaranteed output: the slide puzzle, as it appears after each move
import string # required to use zfill function to print the board
PUZZLE_SIZE = 4 # it is convenient to remember the puzzle's size
# the puzzle, where 0 marks the empty space/cell:
puzzle = [ [15, 14, 13, 12],
[11, 10, 9, 8],
[ 7, 6, 5, 4],
[ 3, 2, 1, 0] ]
# It is convenient to remember which cell is empty:
empty_space = (3, 3)
# loop forever to move the pieces dictated by the user:
while True :
# print the puzzle:
for row in puzzle :
for item in row :
if item == 0 :
print " ",
else :
print string.zfill(item, 2), # print a two-symbol number
print
# ask for the next move:
num = int(raw_input("\nType number of piece to move: "))
# search the puzzle for the piece numbered num:
piece = () # will remember the cell coordinates where num rests
for i in range(PUZZLE_SIZE):
for j in range(PUZZLE_SIZE) :
if num == puzzle[i][j] :
piece = (i, j) # we found num at coordinates i,j
# did we find the piece ?
if piece == () :
print "illegal move --- try again"
else : # we did find it, so let's try to move it:
# check if the piece is adjacent to the empty space:
i = piece[0]
j = piece[1]
if (empty_space == (i-1, j)) \ # to the left ?
or (empty_space == (i+1, j)) \ # to the right ?
or (empty_space == (i, j-1)) \ # above ?
or (empty_space == (i, j+1)) : # below ?
# if True, it's ok to move num into the empty space:
puzzle[empty_space[0]][empty_space[1]] = num
# remember that the former cell holding num is now empty:
puzzle[i][j] = 0
empty_space = (i, j)
else : # False, so it's not ok to move num:
print "illegal move --- try again"
=====================================================
Because we work with a nested list, we require nested loops to print
the list and to search it for the piece that the player wishes to move.
Also, when we check that the piece is adjacent to the empty space,
we must check both the row and the column variations.
puzzle = [15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]Again, the interesting steps in the solution are
find where piece num is situated in the puzzle
once found, verify that it is located adjacent to the empty space (0)
swap num and 0 in the puzzle
To find the desired num in puzzle, we use
an ordinary searching loop:
for i in range(len(puzzle)):
if puzzle[i] == num :
location = i # remember that num is located at position i
break
The most difficult part of the solution is checking that the
position of the piece is adjacent to the empty space.
A first attempt reads somewhat like this:
empty_space = ... # remembers the index of the empty space in the puzzle
if (empty_space == location - 1) \ # to the left ?
or (empty_space == location + 1) \ # to the right ?
or (empty_space == location - ROW_SIZE) \ # above ?
or (empty_space == location + ROW_SIZE) : # below ?
... swap num and 0 in the puzzle ...
else :
... can't move the piece ...
We check whether the empty space is immediately above the position
of the piece to move merely by subtracting the ROW_SIZE --- a
neat trick. (For example, if the piece to be moved rests at
puzzle[7], and the empty space rests at
puzzle[3], then the latter is immediately above the
former.)
Here is the solution based on the above ideas:
FIGURE================================================
# SlidePuzzle
# implements a slide-puzzle game.
# assumed input: a series of integers between 1 and 15, which indicate the
# pieces to move in the slide puzzle
# guaranteed output: the slide puzzle, as it appears after each move
import string # required to use zfill function to print the board
ROW_SIZE = 4 # it is convenient to remember the puzzle's size
# the puzzle, where 0 marks the empty space/cell:
puzzle = [15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
# it is convenient to remember which cell is empty:
empty_space = 15
# loop forever to move the pieces dictated by the user:
while True :
# print the puzzle:
for count in range(len(puzzle)) :
if count % ROW_SIZE == 0 :
print
if puzzle[count] == 0 : # empty space ?
print " ",
else :
print string.zfill(puzzle[count], 2), # print a two-symbol number
# ask for the next move:
num = int(raw_input("\nType number of piece to move: "))
# search the puzzle for the piece numbered num:
location = -1 # will remember the cell where num rests
for i in range(len(puzzle)):
if puzzle[i] == num :
location = i
break
# did we find the piece ?
if location == -1 :
print "illegal move --- try again"
else : # we did find it, so let's try to move it:
# check if the piece is located adjacent to the empty space:
if ((empty_space == location - 1) and (location % ROW_SIZE != 0)) \
or ((empty_space == location + 1) and (empty_space % ROW_SIZE != 0)) \
or (empty_space == location - ROW_SIZE) \
or (empty_space == location + ROW_SIZE) :
# if True, it's ok to move num into the empty space:
puzzle[empty_space] = num
# remember that the former cell holding num is now empty:
puzzle[location] = 0
empty_space = location
else : # False, so it's not ok to move num:
print "illegal move --- try again"
ENDFIGURE===========================================================
The only complication in this solution is the check whether
the piece to be moved rests immediately to the left or to the
right of the empty space: The if-command must be improved to read
if ((empty_space == location - 1) and (location % ROW_SIZE != 0)) \
or ((empty_space == location + 1) and (empty_space % ROW_SIZE != 0)) \
or (empty_space == location - ROW_SIZE) \
or (empty_space == location + ROW_SIZE) :
When the empty space rests at the end of
one row and the piece to be moved rests at the beginning of the next
row, this is not an adjacency. (For example,
the piece to be moved rests at
puzzle[4], and the empty space rests at
puzzle[3], then the latter is not immediately to the left
of the former.)
Either solution is acceptable for the slide puzzle. The nested-list solution requires nested loops for printing and lookup, but it portrays the puzzle in exactly the same dimensions as the real, physical puzzle.
The flat-list solution uses simple techniques for printing and lookup, but there is a small complication when checking whether the piece to be moved is to the left or right of the empty space.
Since each row of the puzzle is itself a list, the puzzle is in fact a list of addresses of lists. This layout is a bit difficult for humans to appreciate, but computers work well with it, because it linearizes the matrix in computer storage, which is itself linear.
The picture shows us one important idea: we must be very careful
when constructing a matrix for the first time. If we try the
``multiplication trick,'' twice, like this:
# INCORRECT attempt to build an 8-by-8 game board:
board = [ [ "" ] * 8 ] * 8
What happens is that
Namespace: | Heap:
|
board : addr2 | addr1: [ "", "", "", "", "", "", "", "" ]
| addr2: [ addr1, addr1, addr1, addr1, addr1, addr1, addr1, addr1 ]
Rather than a 64-celled board, we have an 8-celled one in disguise.
The correct way of building the 64-celled board looks like this:
board = [] # the matrix we will build; starts empty
for i in range(8) :
board.append( [ "" ] * 8 ) # build a new list of 8 cells and
# append it to the matrix
We also learned that some sequences, like an alphabetized string, should be given a data invariant that states the key logical property that is always true about the sequence.
Data invariants are crucial for lists, because lists are mutable. When we alter the value of a cell in a list, we risk ruining the list's data invariant, so we should always state a data invariant for the list and always check that the invariant is kept true when we update the list.
A list's data invariant might be quite simple, such as
numbers = [2, 3, 6, 3, 8, 0] # data invariant: all values in numbers are nonnegative ints
The invariant tells us that we should never encounter, say, a string
within a cell of numbers.
In the case of the slide-puzzle game that we just saw,
the data invariant states
the correct appearance of the slide puzzle:
puzzle = ... # data invariant: puzzle is a permutation of range(16)
That is, puzzle holds the integers 0 to 15 in some mixed up
order.
It is clear that a correctly working slide-puzzle game must preserve the puzzle's data invariant! This must be an invariant property of the loop that reads the human's move and makes the move on the puzzle --- the updated puzzle is still a permutation of the original. Of course, the game's loop must also enforce the primary rule of the slide-puzzle game, which is that only a number adjacent to 0 may be exchanged with the 0.
Sophisticated data invariants can also appear in simple programs.
Consider again the vote-counting program from the beginning of the
chapter:
====================================================
votes = 4 * [0] # data invariant:
# for all i in 0..3, votes[i] == quantity of i's read as input
processing = True
while processing
# invariant: data invariant for votes is preserved
v = int(raw_input("Type your vote (0,1,2,3): ")
if v < 0 or v > 3 :
processing = False # bad vote, so quit
else :
votes[v] = votes[v] + 1
========================================================
The sole purpose of the program is to preserve the list's data invariant
as the input numbers are read one by one. This is not an accident ---
the job of many programs is merely to preserve a data structure's
data invariant.
As a result,
First, tuples are used to build values that are small collections (playing cards and pixels). Tuples are also used to collect values into sequences (collecting words from a sentence or collecting the cards in a card deck).
In contrast, lists are used to build structures like game boards and grids, which have ``spaces'' or ''cells'', can be ``indexed'' by a fixed ``address'', and can be updated with new values. Use a list to build a data structure when
Lists can be unnested (``flat'') or nested (''grids'' or two-dimensional arrays). When we model a linear structure, like a daily timetable, we should use a flat list. It is tempting to use a nested list when we model a gameboard, like a tic-tac-toe board. But often, the computer programming of such a board is simpler with a flat list, and in the case of a slide puzzle or tic-tac-toe board, a flat list works surprisingly well.
When choosing between a flat list and a nested list, are these questions:
For example, a monthly calendar should be modelled with a flat list, even though the calendar is printed as a grid --- there is no relationship between the days (cells) of the month, and we refer to each day with a single index number. In contrast, an 8-by-8 board for playing chess is better modelled as a grid, because chessboard squares are often addressed by row, column coordinates, and some chess pieces move vertically and horizontally, others move diagonally, and others move in the shape of the letter, ''L.'' Computing these forms of movement is done easier with a nested list.
Dictionaries are used to build books, directories, and databases where elements are located by their keys. Use a dictionary when
A list is written with this syntax:
[ ELEMENTS ]
where ELEMENTS are zero of more EXPRESSIONs, separated
by commas. Each expression can compute to any value at all --- number, boolean,
string, tuple, list, etc.
The elements in a list are saved in the list's cells
which are indexed (numbered) by 0, 1, 2, ....
A list can be assigned to a variable, as usual:
gameboard = [ "", "", "", "", "", "", "", "" ]
We can use a shortcut to make a list whose items start with the same value:
gameboard = [ "" ] * 8
Given a list, LIS, we can compute its length (number of cells)
like this:
len( LIS )
The primary operation on lists is indexing, and we can write this indexing
expression:
LIS [ INT_EXPRESSION ]
where LIS is a list, and INT_EXPRESSION is an
expression that computes to an integer that falls between 0 and
len( LIS ) -1. The expression returns the element saved at
cell number INT_EXPRESSION.
We update a list's cell with this assignment command:
LIS [ INT_EXPRESSION ] = EXPRESSION
The assignment destroys the value that was formerly held at cell
INT_EXPRESSION and replaces it with the value of EXPRESSION.
Since a list is a SEQUENCE, we can use the for-loop to
systematically process a list's elements:
for ITEM in LIS :
... ITEM ...
where ITEM is a variable name that stands for each element
from list LIS.
There is a special operation, range, that constructs a
list of numbers: range(NUM) builds the list,
[0, 1, 2, ..., NUM-1]. (E.g., range(3) computes
[0, 1, 2].) We can use range to print a list's
index numbers and contents:
for index in range(len(LIS)) :
print index, LIS[index]
Here are two methods that alter lists:
s1 = " this is a sentence." words = s1.split() print wordsprints ['this', 'is', 'a', 'sentence.']
time = "12:35:49"
words = time.split(":")
print words
prints ['12', '35', '49'].
Lists can be nested inside lists. Here is how to build an 8-by-8 chessboard, a matrix:
board = [ ]
for row in range(8) :
board.append([ "" ] * 8)
We assign to individual cells of the board with two indexes:
board[5][5] = ("white", "pawn")
and we use nested for-loops to print the board:
for row in board :
for square in row :
print square, "|",
print
A dictionary is written with this syntax:
{ KEY_ELEMENT_PAIRS }
where KEY_ELEMENT_PAIRS are zero or more KEY : ELEMENTs,
separated by commas.
Each KEY must be an immutable value (number, boolean, string,
or tuple).
Each ELEMENT can compute to any value at all --- number, boolean,
string, list, dictionary, etc.
The elements in a list are saved in a hash table structure.
A dictionary can be assigned to a variable, as usual.
Given a dictionary, DICT, we can find an element by using
its key:
DICT [ KEY ]
If KEY is not found in DICT, it is an error,
so it is better to ask first if the KEY is present:
if KEY in DICT :
... DICT[KEY] ...
We update a dictionary with this assignment command:
DICT [ KEY ] = EXPRESSION
If the KEY is new to DICT, then a new key, element
pair is added. If the KEY is already in use,
the assignment destroys the value that was formerly associated with
KEY and replaces it with the value of EXPRESSION.
We can use the for-loop to
systematically process a dictionary:
for K in DICT :
... K ... DICT[K] ...
where K is a variable name that stands for each key saved
in dictionary DICT.
The operation, del DICT[K] deletes key K and its element from DICT. (If K is not in DICT, it is an error.)
Here are two useful methods for dictionaries:
keylist = my_dictionary.keys()
keylist.sort()
for k in keylist:
print k, ":", my_dictionary[k]