Notice the relationship between the equations and the class diagram. Notice also the "backwards" arc from Folder to Entry, stating that "an Entry can be a Folder which itself holds Entries."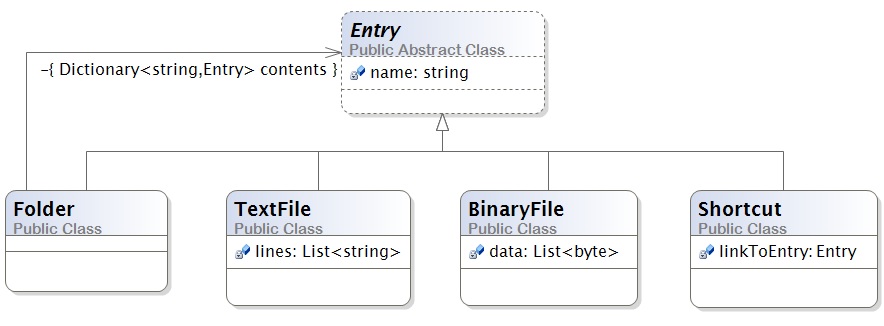
If you are a C-programmer, your world consists of ints, pointers (storage addresses), and linear arrays. As a convenience, the C-compiler lets you define matrices and structs, but these are really just linear arrays with a complex layout. You must learn modelling tricks for all other types of data.
If you are a script programmer (Javascript, Python, Ruby, ...), your world is that of ints, strings, tuples, lists (arrays that grow and shrink), and dictionaries (hash tables whose keys can be "nonmutable" data values). You must learn modelling tricks for all other types of data.
If you are a Java/C# programmer, your world is C but with a class construction, which is nothing more than a struct that holds both variable declarations (fields) and methods. As a convenience, you are given libraries with complex names and methods for faking lists and dictionaries. You must learn modelling tricks for all other types of data.
Real-life data rarely matches the data types given to you by your language. Real data tends to be grouped in "layers" or "levels" with possible "horizontal" or "cross-level" references (linkages). It is critical that a C#/Java programmer learn to model layered data types. There are two relevant design patterns.
Entry = Textfile || Binaryfile || Shortcut || Folder Textfile = List<char> Binaryfile = List<int> Shortcut = pointerTo(Entry) Folder = Dictionary<string, Entry> FileSystem = FolderThese equations define a data type in many functional programming languages (Standard ML, Haskell, OCAML, Scala's pattern language), but we must manually model the composite definition in an object language.
The Composite design pattern is the scheme we use to convert a layered data type definition into class-based code. Here is the class diagram that
defines "type" Entry.
We use an abstract class (incomplete class) to name Entry.
Notice the relationship between the equations and the class diagram.
Notice also the "backwards" arc from Folder to Entry, stating that "an Entry can be a Folder which itself holds Entries."

Here is the code corresponding to the class diagram. The composite type's name is coded as an abstract class (an "unfinished class") that holds an Entry's name. The rest of an entry is filled in by one of the four options that extend/finish the abstract class:
===================================================
// the base name of the composite type:
public abstract class Entry {
protected string name; // the entry's name; accessible to the subclass code
// get and set the value of name:
public string Name {
get { return name; }
set { name = value; }
}
}
// models a text file as a sequence (list) of strings
public class TextFile: Entry {
private List<string> lines;
public TextFile(string name) {
base.name = name; // stores the name in the class Entry part of this object
lines = new List<string>(); // file is empty at the start
}
//methods to add a line and to return all the lines of the file:
public void addLine(string s) { lines.Add(s); }
public List<string> Lines { get { return lines; } }
}
// models a link (shortcut) to an Entry not in the present folder/level
public class Shortcut: Entry {
public readonly Entry link;
public Shortcut(string name, Entry link) {
base.name = name;
this.link = link;
}
}
// models a folder as a directory of Entries, indexed by their names:
public class Folder : Entry {
private Dictionary<string, Entry> directory;
public Folder(string name) {
base.name = name; // save name in class Entry part of this object
directory = new Dictionary<string, Entry>(); // initially, folder is empty
}
// returns the Entry with name. If name is bogus, returns null.
public Entry find(string name) {
Entry ans = null;
if (directory.ContainsKey(name)) { ans = directory[name]; }
return ans;
}
// adds a new Entry, e, to this folder
public void add(Entry e) {
if (!directory.ContainsKey(e.Name)) {
directory[e.Name] = e; }
}
// returns a list of all the Entry objects saved in this folder
public List<Entry> getListing() {
List<Entry> ans = new List<Entry>();
foreach (var pair in directory) { ans.Add(pair.Value); }
return ans;
}
}
===================================================
Say that a file system consists of a folder, F, that holds
textfile, t.txt, binary file, b.exe, and folder G.
G itself holds folder H, which holds u.txt.
The objects constructed from the above classes to implement the file system would look like this:
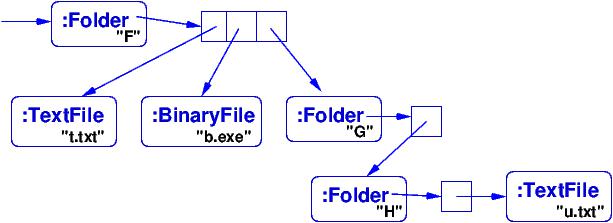
Say that we must print the names of all the entries in the file system, a standard traversal activity. We define a traversal method that "opens up" the levels of the file-system object that it traverses, using a recursive call (self-call, a restart of a fresh copy of the method) to open up each inner level.
Here is a method that collects the names of all the contents of the file system.
It should be inserted into class Entry:
// returns a string that lists the name of the current entry and the names of
// all the Entries within it, if any.
// Note that this refers to the object being analyzed.
public string contents() {
string ans = this.Name;
if (this is TextFile) { // asks if this object was constructed from class TextFile
ans = ans + " is a text file\r\n";
}
else if (this is Shortcut) {
ans = ans + " is a shortcut\r\n";
}
else if (this is Folder) {
ans = ans + " is a folder containing:\r\n";
List<Entry> contents = ((Folder)this).getListing(); // get all entries in the folder
foreach (Entry item in contents) { // get contents of all the entries...
ans = ans + item.contents();
}
}
return ans;
}
So, if the file-system object is fileSystem, the call,
fileSystem.contents() will open up the levels of fileSystem and print
all the names therein.
Game boards are constructed to have data type, Area. If you look at the code and the object diagram for the file system example, you can visualize a layered game-board layout for an adventure game based on exploring Areas.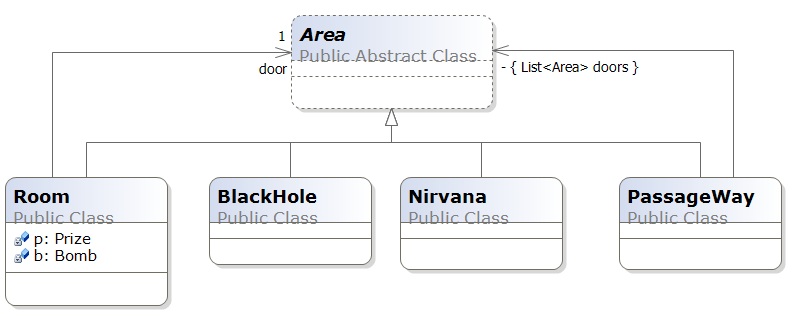
Here is a possible definition of a spelling tree for word completion:
This layered data type can be modelled with just one class, which holds handles to zero of more inner levels of its own class.
Here is the code for class Path:
===================================================
// models a partial/complete word, entered as a sequence ("path") of chars
public class Path {
private string word; // the sequence of chars, e.g., "cat"
private int count; // how many times this sequence has been used as a completed word
private Dictionary<char, Path> suffixes; // extensions of this word, e.g., "cats" (indexed by 's') or "cattle" (indexed by 't')
public Path(string wordSoFar) {
word = wordSoFar; count = 0;
suffixes = new Dictionary<char, Path>();
}
// "get" methods:
public string getWord() { return word; }
public int getCount() { return count; }
// notify this Path that its word is complete and used in the user's document
public void finishedWord() { count++; }
// add another letter, c, to the word being typed and return path of word+c
public Path addLetter(char c) {
Path ans = null;
if (suffixes.Contains(c)) {
ans = suffixes[c];
}
else {
ans = new Path(word + c);
suffixes[c] = ans;
}
return ans;
}
// returns handle to path for this word+c. If none exists, returns null
public Path findNextLetter(char c) {
Path ans = null;
if (suffixes.Contains(c)) { ans = suffixes[c]; }
return ans;
}
}
===================================================
Here's how we add words to the spelling tree:
Path spellingTree = new Path("");
string inputText = "cats cannot catch cold quickly";
string[] words = inputText.split(' '); // divide text into its 5 words
foreach (string w in words) { // add w to spellingTree:
Path path = spellingTree;
foreach(char c in w) {
path = path.addLetter(c);
}
path.finishedWord(); // increment count for w
}
This method queries
spellingTree for word counts, e.g., spellingTree.countOf("cats"):
public int countOf(string word) {
Path p = this; // start counting at the root of this tree
foreach (char c in word) { // search tree for word, one char at a time:
p = p.findNextLetter();
if (p == null) { return 0; } // word isn't found
}
// else, we found word in the tree, so
return p.countOf();
}
When we use a GUI to communicate with a software system, we are using a kind of "point and nudge" language, like humans use when they don't want to speak words to one another.
More intelligent communication can be made with words than with "point and nudge", and sophisticated software systems use word-based "command languages" for input. Examples of command languages are bash, for talking to an operating system; SQL DML, for asking queries to a database; and Javascript, for talking to a web browser.
Languages based on words have internal phrase structure, which is naturally expressed by a composite data type. (E.g., "a sentence consists of a subject phrase and a predicate phrase, where the subject phrase has a noun and a modifier phrase and the predicate phrase has a verb, a modifier phrase, and optional direct-object and indirect-object phrases, ...".)
We saw in the previous section how a method uses self-calls (recursions) to open the inner levels of an object. This is again the case for language processing: an interpreter is a method that calculates the meaning/actions of a command by opening the command with recursive calls.
Interpreters are so important to modern-day programming that the name, "interpreter design pattern", was coined to emphasize this implementation technique.
In the 1950s, Noam Chomsky realized that the syntax of a sentence can be represented by a tree, and the rules for building syntactically correct sentences can be written as an equational, inductive definition. Chomsky called the definition a grammar. (John Backus and Peter Naur independently discovered the same concept, and for this reason, a grammar is sometimes called BNF (Backus-Naur form) notation.)
A grammar is a set of equations (rules), where each equation defines a set of phrases (strings of words).
Say we wish to define precisely how to write
arithmetic expressions, which consist
of numerals composed with addition and subtraction operators.
Here are the equations (rules)
that define the syntax of arithmetic expressions:
===================================================
EXPRESSION ::= NUMERAL | ( EXPRESSION OPERATOR EXPRESSION )
OPERATOR ::= + | -
NUMERAL is a sequence of digits from the set, {0,1,2,...,9}
===================================================
The words in upper-case letters (nonterminals)
name phrase and word forms:
an EXPRESSION phrase consists
of either a NUMERAL word
or
a left paren followed by another (smaller) EXPRESSION
phrase followed by an OPERATOR word
followed by another (smaller) EXPRESSION phrase
followed by a right paren.
(The vertical bar means ``or.'')
If the third equation is too informal for you, we can replace it with
these two:
NUMERAL ::= DIGIT | DIGIT NUMERAL
DIGIT ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
but usually the spelling of individual words is stated informally,
like we did originally.
Using the rules, we can verify that this sequence of symbols is
a legal EXPRESSION phrase:
(14 - (3 + 2))
Here is the explanation, stated in words:
There is a compact representation of an arithmetic sentence, as an operator tree. Here is the operator tree for (4 - (3 + 2)):
-
/ \
4 +
/ \
3 2
An operator tree places the "operator" or "verb" at the top of each "phrase" (subtree).
An operator tree for arithmetic has two forms, which we can define
precisely with its own BNF rule, like this:
TREE ::= NUMERAL | OP
/ \
TREE TREE
OP ::= + | -
NUMERAL ::= a string of digits
That is, every operator tree is either just a single numeral
or a tree holding an operator symbol and two subtrees.
This is clearly a composite type whose code looks like this:
===================================================
public abstract class Expression { }
public class NumeralTree : Expression {
public readonly string theNumeral;
...
}
public class ExpressionTree : Expression {
public readonly string operator; // should be "+" or "-"
public readonly Expression left;
public readonly Expression right;
...
}
===================================================
A parser reads a string like (14 - (2 + 3)) and generates this
operator tree:
Expression tree = new ExpressionTree("-",
new NumeralTree("14"),
new ExpressionTree("+",
new NumeralTree("2"),
new NumeralTree("3")))
===================================================
When a compiler or interpreter processes a computer program, it first builds the
program's operator tree. Then, it
calculates the meaning --- the semantics --- of the
tree.
Here is the interpreter for the arithmetic language. It computes on the operator tree representation of the arithmetic program:
===================================================
public int interpretTree(Expression t) {
int meaning = -1;
if (t is Numeral) {
meaning = Convert.ToInt32(t.theNumeral);
}
else if (t is ExpressionTree) {
int leftmeaning = interpretTree(t.left);
int rightmeaning = interpretTree(t.right);
if (t.operator == "+") {
meaning = leftmeaning + rightmeaning;
} else if (t.operator == "-") {
meaning = leftmeaning + rightmeaning;
}
return meaning;
}
===================================================
The function's recursions match the recursions in the grammar
rule/composite data type that defines the set of operator trees.
The recursion computes the numerical meanings
of the subtrees and combines them to get the meaning of
the complete tree.