 ===================================================
===================================================When I speak to you, how do you understand what I am saying? First, it is important that we communicate in a common language, say, English, and it is important that I speak in grammatically correct English (e.g., ``Eaten house horse before.'' is a grammatically incorrect, useless communication). Finally, you must know how to attach meanings to the words and phrases that I use.
The same ideas are just as important when you talk to a computer, by means of a program written in a programming language. For the computer to understand what you say, the computer must have knowledge of the language you use. This includes:
In the 1950s, Noam Chomsky realized that the syntax of a sentence (or computer program) can be represented as a tree, and the rules for building syntactically correct sentences can be written as an equational, inductive definition. Chomsky called the definition a grammar. (John Backus and Peter Naur independently discovered the same notation, and for this reason, a grammar is sometimes called BNF (Backus-Naur form) notation.)
Grammars are best introduced by example.
===================================================
EXPRESSION ::= NUMERAL | ( EXPRESSION OPERATOR EXPRESSION )
OPERATOR is + or -
NUMERAL is a sequence of digits from the set, {0,1,2,...,9}
===================================================
The words in upper-case letters (nonterminals)
name phrase and word forms:
an EXPRESSION phrase consists
of either a NUMERAL word
or
a left paren followed by another (smaller) EXPRESSION
phrase followed by an OPERATOR word
followed by another (smaller) EXPRESSION phrase
followed by a right paren.
(The vertical bar means ``or.'')
(We can also write equations for OPERATOR and NUMERAL, like this:
OPERATOR ::= + | -
NUMERAL ::= DIGIT | DIGIT NUMERAL
DIGIT ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
but usually the spelling of individual words is stated informally,
like we did above.)
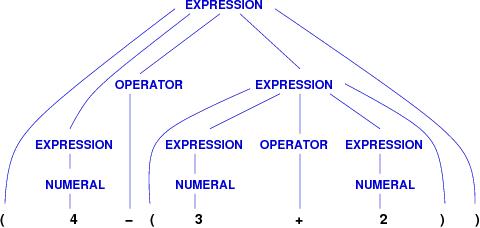
Using the rules, we can verify that this sequence of words is
a legal EXPRESSION phrase:
(4 - (3 + 2))
There is a precise formal justification:
===================================================Indeed, a sequence of words is an EXPRESSION phrase if and only if one can build a derivation tree for the words using the grammar rules.===================================================
=================================================== PROP ::= TERM BINOP TERM | TERM TERM ::= UNOP FACTOR | FACTOR FACTOR ::= PRIM | ( PROP ) BINOP ::= ^ | v | --> UNOP ::= ~ PRIM is a word that begins with a letter ===================================================Here is the derivation tree for an example, (A v B) --> ~C:
As the previous examples show, spaces within the grammar rules do not imply that spaces are required within the phrases defined by the rules.
===================================================
PROGRAM ::= COMMANDLIST
COMMANDLIST ::= COMMAND | COMMAND ; COMMANDLIST
COMMAND ::= VAR = EXPRESSSION
| print VARIABLE
| while EXPRESSION : COMMANDLIST end
EXPRESSION ::= NUMERAL | VAR | ( EXPRESSION OPERATOR EXPRESSION )
OPERATOR is + or -
NUMERAL is a sequence of digits from the set, {0,1,2,...,9}
VAR is a string beginning with a letter, not 'print', 'while', or 'end'
===================================================
The definition says that a program is a list (sequence) of commands,
which can be assignments or prints or while-loops. The body
of a while-loop is itself a list of commands.
The grammar does not explain what the phrases mean, so we cannot
determine here how a command like, while x : x = (x - 1); y = x end,
operates.
You should draw the derivation trees for these PROGRAMs:
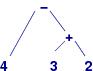
Here is the operator tree that is produced from the
derivation tree for (4 - (3 + 2)):
It is called an ``operator tree'' because the operators rest
in the places where the phrase names once appeared.
It's lots more compact than the original derivation tree,
but it has the same branching structure, which is the crucial part.
Operator trees can be easily implemented in most computer languages.
When
use a dynamic data-structures language, like Python (or Scheme or Prolog or ML),
we can build nested lists and we can represent an operator
tree as a nested list. Here is the nested-list representation
of the above operator tree:
["-", "4", ["+", "3", "2"]]
Here is another example: For ((2+1) - (3-4)), we have this operator
tree (nested list):
["-", ["+", "2", "1"], ["-", "3", "4"]]
For the proposition example,
(A v B) --> ~C, its operator tree is
["-->", ["v", "A", "B"], ["~", "C"]]
Finally, this program,
x = 3; while x : x = (x -1) end; print x,
has this operator tree:
[["=", "x", "3"],
["while", "x", [["=", "x", ["-", "x", "1"]]]],
["print", "x"]
]
We work with the nested-list format of operator trees from here on.
When a compiler processes a program, it first builds the program's operator tree. Then, it calculates the meaning --- the semantics --- of the tree. The process of giving meaning is done with a recursively defined tree-traversal function.
Let's learn this technique on the operator trees for expressions.
An expression operator tree has only two forms, which we define
precisely yet again with a grammar rule:
ETREE ::= NUMERAL | [ OP, ETREE_1, ETREE_2 ]
where NUMERAL is a string of digits
and OP is either "+" or "-"
That is, every binary operator tree is either just a single numeral string
or a list holding an operator symbol and two subtrees.
We wish to traverse completely a binary operator tree and compute its
entire meaning. To do this,
we write a function that implements
a recursion that matches the recursion in the grammar rule.
The pattern of recursion looks like this:
def process(etree) :
"""process traverses all the subparts of operator tree etree: """
if etree is an instance of a NUMERAL :
ans = ... compute the meaning of the NUMERAL string ...
else : # etree is an instance of [OP, ETREE1, ETREE2]
op = etree[0]
subans1 = process(etree[1])
subans2 = process(etree[2])
ans = ... assemble op, subans1, and subans2 into its meaning ...
return ans
The process function uses recursion to process the smaller trees,
etree[1] and etree[2] embedded within etree to get their answers,
and then it computes on these answers for its own answer.
Let's write an evaluator to compute the integer value represented by
an operator tree.
(For example,
["-", ["+", "2", "1"], ["-", "3", "4"]] computes to the integer, 4.)
Here is the function that evaluates an operator tree to its
integer meaning:
===================================================
def eval(t) :
"""pre: t is an ETREE,
where ETREE ::= NUMERAL | [ OP, ETREE1, ETREE2 ]
NUMERAL is a string, and OP is "+" or "-"
post: ans is the numerical meaning of t
"""
if isinstance(t, str) and t.isdigit() : # is t a NUMERAL (string of digits)?
ans = int(t)
else : # t is a list, [op, t1, t2]
op = t[0]
t1 = t[1]
t2 = t[2]
ans1 = eval(t1)
# assert: ans1 is the numerical meaning of t1
ans2 = eval(t2)
# assert: ans2 is the numerical meaning of t2
if op == "+" :
ans = ans1 + ans2
elif op == "-" :
ans = ans1 - ans2
return ans
===================================================
Here is a sketch of the execution of
eval( ["-", ["+", "2", "1"], ["-", "3", "4"]] ),
which computes to 3 - (-1) == 4:
===================================================
eval( ["-", ["+", "2", "1"], ["-", "3", "4"]] )
=> op = "-"
t1 = ["+", "2", "1"]
t2 = ["-", "3", "4"]
ans1 = eval(t1) => op = "+"
t1 = "2"
t2 = "1"
ans1 = eval(t1) => ans = 2
= 2
ans2 = eval(t2) => ans = 1
= 1
ans = 2+1 = 3
= 3
ans2 = eval(t2) => op = "-"
t1 = "3"
t2 = "4"
ans1 = eval(t1) => ans = 3
= 3
ans2 = eval(t2) => ans = 4
= 4
ans = 3-4 = -1
= -1
ans = 3 - (-1) = 4
= 4
===================================================
Each => represents a recursive call (restart)
of eval on a subtree of the original
operator tree. Each restart keeps its own namespace
of its local variables, which it uses to compute the answer for its subtree.
Eventually, the answers are returned and combined.
You can see that the pattern of calls to eval matches
the pattern of structure in the original operator tree.
Recursive processing can be used on operator trees for
any grammar at all. Let's review the grammar for the mini-programming
language:
===================================================
PROGRAM ::= COMMANDLIST
COMMANDLIST ::= COMMAND | COMMAND ; COMMANDLIST
COMMAND ::= VAR = EXPRESSSION
| print VARIABLE
| while EXPRESSION : COMMANDLIST end
EXPRESSION ::= NUMERAL | VAR | ( EXPRESSION OPERATOR EXPRESSION )
OPERATOR is + or -
NUMERAL is a sequence of digits from the set, {0,1,2,...,9}
VAR is a string beginning with a letter; it cannot be 'print', 'while', or 'end'
===================================================
For program,
x = 3 ; while x : x = x - 1 end ; print x
here is its operator tree:
[["=", "x", "3"],
["while", "x", [["=", "x", ["-", "x", "1"]]]],
["print", "x"]
]
The operator tree has three ``levels'' --- a commandlist level,
a command level, and an
expression level, so it is better for us to keep these separate
and say that operator trees look like this:
CLIST ::= [ CTREE+ ]
where CTREE+ means one or more CTREEs
CTREE ::= ["=", VAR, ETREE] | ["print", VAR] | ["while", ETREE, CLIST]
ETREE ::= NUMERAL | VAR | [OP, ETREE1, ETREE2]
where OP is either "+" or "-"
Now, we write three functions: one for CLIST trees,
one for CTREEs, and one for ETREEs.
This set of functions is called
an interpreter. It is like the interpreter that underlies
the computer implementation of Python and Java.
It defines the semantics of the sentences in the computer language.
Here is the interpreter for the programming language;
it reads an operator tree and computes the meaning (executes
the commands) of the tree.
It would be best for you to note
first the global variable, memory, then study interpretETREE
(which works like eval above), and then study
interpretCTREE, which executes the assignment, print, and
while-commands:
===================================================
memory = {} # a global variable that holds the values of the VARIABLES
# used in program, p. It is implemented as a Python dictionary.
def interpretCLIST(p) :
"""pre: p is a program represented as a CLIST ::= [ CTREE+ ]
where CTREE+ means one or more CTREEs
post: memory holds all the updates commanded by program p
"""
for command in p :
interpretCTREE(command)
def interpretCTREE(c) :
"""pre: c is a command represented as a CTREE:
CTREE ::= ["=", VAR, ETREE] | ["print", VAR] | ["while", ETREE, CLIST]
post: memory holds all the updates commanded by c
"""
operator = c[0]
if operator == "=" : # assignment command
var = c[1]
exprval = interpretETREE(c[2])
memory[var] = exprval
elif operator == "print" : # print command
print memory[c[1]]
elif operator == "while" : # while command
expr = c[1]
body = c[2]
while (interpretETREE(expr) > 0) :
interpretCLIST(body)
else : # error
crash("invalid command")
def interpretETREE(e) :
"""pre: e is an expression represented as an ETREE:
ETREE ::= NUMERAL | VAR | [OP, ETREE1, ETREE2]
where OP is either "+" or "-"
post: ans holds the numerical value of e
"""
if isinstance(e, str) and e.isdigit() : # a numeral
ans = int(e)
elif isinstance(e, str) and len(e) > 0 and e[0].isalpha() : # var name
if e in memory :
ans = memory[e]
else :
crash("variable name undefined")
else : # [op, e1, e2]
op = e[0]
ans1 = interpretETREE(e[1])
ans2 = interpretETREE(e[2])
if op == "+" :
ans = ans1 + ans2
elif op == "-" :
ans = ans1 - ans2
else :
crash("illegal arithmetic operator")
return ans
def crash(message) :
"""pre: message is a string
post: message is printed and interpreter stopped
"""
print message + "! crash! core dump: ", memory
raise Exception # stops the interpreter
===================================================
To start the interpreter with a program, type
interpretCLIST(p), where p is a program represented as an operator
tree. For example,
interpretCLIST([["=", "x", "3"],
["while", "x", [["=", "x", ["-", "x", "1"]]]],
["print", "x"]
])
will assign 3 to "x" in global variable, memory;
will next decrement "x"'s value from 3 to 2 to 1 to 0
and stop the loop;
and will print x's final value in memory, namely, 0.
The interpreter works just like Python's and Java's work.
In particular, intepretCOMMAND shows that the semantics
of the while-command is that the expression part is repeatedly
evaluated, then the body part, as long as the expression part
evaluates to an int that is positive.
Another use of recursively defined functions is for translation,
the systematic rewriting of a program from one language to another.
Here is an example, where we process an operator tree to assemble
the postfix-string representation of the tree:
===================================================
def postfix(t) :
"""pre: t is a TREE, where TREE ::= NUM | [ OP, TREE1, TREE2 ]
post: ans is a string holding a postfix (operator-last) sequence
of the symbols within t
"""
if isinstance(t, str) : # is t an instance of a NUM (a simple string) ?
ans = t # the postfix of a NUM is just the NUM itself
else : # t is a list, [op, t1, t2], that is, isinstance(t, list)
op = t[0]
t1 = t[1]
t2 = t[2]
ans1 = postfix(t1)
# assert: ans1 is a string holding the postfix form of t1
ans2 = postfix(t2)
# assert: ans2 is a string holding the postfix form of t2
ans = ans1 + ans2 + op # the answer combines the subanswers
# assert: ans holds the postfix form of t
return ans
===================================================
The function's recursions matches exactly the recursions in the grammar
rule that defines the set of operator trees.
For example, postfix(["+", ["-", 2, 1], 4]) builds the postfix
string, "21-4+". We can draw the results of the function call like
this:
===================================================
postfix(["+", ["-", "2", "1"], "4"])
=> op = "+"
t1 = ["-", "2", "1"]
t2 = "4"
ans1 = postfix(t1) => op = "-"
t1 = "2"
t2 = "1"
ans1 = postfix(t1) => ans = "2"
= "2"
ans2 = postfix(t2) => ans = "1"
= "1"
ans = "2" + "1" + "-"
= "21-"
= "21-"
ans2 = postfix(t2) => ans = "4"
= "4"
ans = "21-" + "4" + "+"
= "21-4+"
===================================================
Each => represents a recursive call (restart)
of postfix on a subtree of the original
operator tree. Each restart keeps its own copy (namespace)
of its local variables, which it uses to compute the answer for its subtree.
Eventually, the answers are returned and combined.
You can see that the pattern of calls to postfix matches
the structure in the original operator tree.
If the previous explanation was not enough for you, you can
insert print commands into postfix so that the computer
shows you the path it takes to analyze an operator tree:
===================================================
def postfixx(t, level = 0) :
"""pre: t is a TREE, where TREE ::= INT | [ OP, TREE1, TREE2 ]
level is an int, indicating at what depth t is situated
in the overall tree being postfixxed
post: ans is a string holding a postfix (operator-last) sequence
of the symbols within t
"""
print level * " ", "Entering subtree t=", t
if isinstance(t, str) : # is t a numeral?
ans = str(t)
else : # t is a list, [op, t1, t2]
op = t[0]
t1 = t[1]
t2 = t[2]
ans1 = postfixx(t1, level + 1)
ans2 = postfixx(t2, level + 1)
ans = ans1 + ans2 + op # the answer combines the two subanswers
print level * " ", "Exiting subtree t=", t, " ans=", ans
print
return ans
===================================================
If you call this function, say, postfixx(["+", "2" , ["-", "3" , "4"]]),
you will see this printout:
===================================================
Entering subtree t= ['+', '2', ['-', '3', '4']]
Entering subtree t= 2
Exiting subtree t= 2 ans= 2
Entering subtree t= ['-', '3', '4']
Entering subtree t= 3
Exiting subtree t= 3 ans= 3
Entering subtree t= 4
Exiting subtree t= 4 ans= 4
Exiting subtree t= ['-', '3', '4'] ans= 34-
Exiting subtree t= ['+', '2', ['-', '3', '4']] ans= 234-+
===================================================
This shows that the computer descended into the levels of the tree
from left to right, computing answers for its leaves that were combined
into an answer for the entire tree.
We can also do translations from one form of tree to another form of tree.
For example, maybe we wish to reformat our operator trees so that the operator
comes last in the list representation:
PTREE ::= NUM | [ PTREE1, PTREE2, OP ]
so that postfixTree(["+", "2" , ["-", "3" , "4"]]) returns this PTREE:
["2" , ["3" , "4", "-"], "+"]. Here's how we use the recursion pattern:
===================================================
def postfixTree(t) :
"""pre: t is a TREE, where TREE ::= NUM | [ OP, TREE1, TREE2 ]
post: ans is t reformatted as a PTREE so that the operators are last:
PTREE ::= NUM | [ PTREE1, PTREE2, OP ]
"""
if isinstance(t, str) : # is t an instance of a NUM (a simple string)?
ans = t # just the NUM itself
else : # t is a list, [op, t1, t2], that is, isinstance(t, list)
op = t[0]
ans1 = postfixTree(t[1])
# assert: ans1 is the PTREE form of t[1]
ans2 = postfixTree(t[2])
# assert: ans2 is the PTREE form of t[2]
ans = [ans1, ans2, op] # combine the subanswers into a PTREE
# assert: ans holds the PTREE form of t
return ans
===================================================
A compiler for a programming language like Java or C# does a series of such translations to convert Java code into internal trees into byte code: (i) the original Java program is translated into an operator tree; (ii) the operator tree is translated into a nested-list representation, the representation is simplified further, and it is translated into a list of three-address code; (iii) the tree-address code is translated into a long string called byte code.
For example, say we want a program that can read a line of text, like ((2+1) - (3 - 4) ), and build the operator tree, ["-", ["+", "2", "1"], ["-", "3", "4"]]. The program's algorithm will go like this:
For the first step, here is a little function that disassembles
a line of text and makes a list of words that were found in the text:
===================================================
def scan(text) :
"""scan splits apart the symbols in text into a list.
pre: text is a string holding a proposition
post: answer is a list of the words and symbols within text
(spaces and newlines are removed)
"""
OPERATORS = ("(", ")", "+", "-", ";", ":", "=") # must be one-symbol operators
SPACES = (" ", "\n")
SEPARATORS = OPERATORS + SPACES
nextword = "" # the next symbol/word to be added to the answer list
answer = []
for letter in text:
# invariant: answer + nextword + letter equals all the words/symbols
# read so far from text with SPACES removed
# see if nextword is complete and should be appended to answer:
if letter in SEPARATORS and nextword != "" :
answer.append(nextword)
nextword = ""
if letter in OPERATORS :
answer.append(letter)
elif letter in SPACES :
pass # discard space
else : # build a word or numeral
nextword = nextword + letter
if nextword != "" :
answer.append(nextword)
return answer
===================================================
For example, scan("((2+1) - (3 - 4) )") returns as its answer,
['(', '(', '2', '+', '1', ')', '-', '(', '3', '-', '4', ')', ')'].
Now, we use the grammar rule to guide us to writing the
function that reads the list of words and constructs the operator tree.
Here is the grammar rule for arithmetic expressions:
EXPRESSION ::= NUMERAL | VAR | ( EXPRESSION OPERATOR EXPRESSION )
where OPERATOR is "+" or "-"
NUMERAL is a sequence of digits
VAR is a string of letters
For each construction in the grammar rule,
there is an operator tree to build:
for NUMERAL, the tree is NUMERAL
for VAR, the tree is VAR
for ( EXPRESSION_1 OPERATOR EXPRESSION_2 ), the tree is [OPERATOR, T1, T2]
where T1 is the tree for EXPRESSION_1
T2 is the tree for EXPRESSION_2
We write a function, parseEXPR, that reads the words of an arithmetic
expression and builds the tree, based on the words. Like the eval function
seen earlier, the grammar rules show us what to do.
It is simplest to use these global variables and a helper function
to parcel out the input words one at a time:
===================================================
# say that inputtext holds the text that we must parse into a tree:
wordlist = scan(inputtext) # holds the remaining unread words
nextword = "" # holds the first unread word
# global invariant: nextword + wordlist == all remaining unread words
EOF = "!" # a word that marks the end of the input words
getNextword() # call this function to move the first word into nextword:
def getNextword() :
"""moves the front word in wordlist to nextword.
If wordlist is empty, sets nextword = EOF
"""
global nextword, wordlist
if wordlist == [] :
nextword = EOF
else :
nextword = wordlist[0]
wordlist = wordlist[1:]
===================================================
The function that builds expression-operator trees looks like this:
===================================================
def parseEXPR() :
"""builds an EXPR operator tree from the words in nextword + wordlist,
where EXPR ::= NUMERAL | VAR | ( EXPR OP EXPR )
OP is "+" or "-"
also, maintains the global invariant (on wordlist and nextword)
"""
if nextword.isdigit() : # a NUMERAL ?
ans = nextword
getNextword()
elif isVar(nextword) : # a VARIABLE ?
ans = nextword
getNextword()
elif nextword == "(" : # ( EXPR op EXPR ) ?
getNextword()
tree1 = parseEXPR()
op = nextword
if op == "+" or op == "-" :
getNextword()
tree2 = parseEXPR()
if nextword == ")" :
ans = [op, tree1, tree2]
getNextword()
else :
error("missing )")
else :
error("missing operator")
else :
error("illegal symbol to start an expression")
return ans
def isVar(word) :
"""checks whether word is a legal variable name"""
KEYWORDS = ("print", "while", "end")
ans = ( word.isalpha() and not(word in KEYWORDS) )
return ans
def error(message) :
"""prints an error message and halts the parse"""
print "parse error: " + message
print nextword, wordlist
raise Exception
===================================================
Function parseEXPR uses the grammar rule to ask the appropriate questions
about nextword, the next input word, to decide which form of operator
tree to build. It is not an accident that the grammar rule for
EXPRESSION is defined so that each of the three choices for an expresion
begins with a unique word/symbol. This is the key to
choosing the appropriate form of tree to build.
We tie the pieces together like this:
===================================================
# global invariant: nextword + wordlist == all remaining unread words
nextword = "" # holds the first unread word
wordlist = [] # holds the remaining unread words
EOF = "!" # a word that marks the end of the input words
def main() :
global wordlist
# read the input text, break into words, and place into wordlist:
text = raw_input("Type an arithmetic expression: ")
wordlist = scan(text)
# do the parse:
getNextword()
tree = parseEXPR()
print tree
if nextword != EOF :
error("there are extra words")
===================================================
===================================================
def parseCOMMAND() :
"""builds a COMMAND operator tree from the words in nextword + wordlist,
where COMMAND ::= VAR = EXPRESSSION
| print VARIABLE
| while EXPRESSION : COMMANDLIST end
also, maintains the global invariant (on wordlist and nextword)
"""
if nextword == "print" : # print VARIABLE ?
getNextword()
if isVar(nextword) :
ans = ["print", nextword]
getNextword()
else :
error("expected var")
elif nextword == "while" : # while EXPRESSION : COMMANDLIST end ?
getNextword()
exprtree = parseEXPR()
if nextword == ":" :
getNextword()
else :
error("missing :")
cmdlisttree = parseCMDLIST()
if nextword == "end" :
ans = ["while", exprtree, cmdlisttree]
getNextword()
else :
error("missing end")
elif isVar(nextword) : # VARIABLE = EXPRESSION ?
v = nextword
getNextword()
if nextword == "=" :
getNextword()
exprtree = parseEXPR()
ans = ["=", v, exprtree]
else :
error("missing =")
else : # error -- bad command
error("bad word to start a command")
return ans
===================================================
We finish with the function that collects the commands in a COMMANDLIST:
===================================================
def parseCMDLIST() :
"""builds a COMMANDLIST tree from the words in nextword + wordlist,
where COMMANDLIST ::= COMMAND | COMMAND ; COMMANDLIST
that is, one or more COMMANDS, separated by ;s
also, maintains the global invariant (on wordlist and nextword)
"""
anslist = [ parseCOMMAND() ] # parse first command
while nextword == ";" : # collect any other COMMANDS
getNextword()
anslist.append( parseCOMMAND() )
return anslist
def main() :
"""reads the input mini-program and builds an operator tree for it,
where PROGRAM ::= COMMANDLIST
Initializes the global invariant (for nextword and wordlist)
"""
global wordlist
text = raw_input("Type the program: ")
wordlist = scan(text)
getNextword()
# assert: invariant for nextword and wordlist holds true here
tree = parseCMDLIST()
# assert: tree holds the entire operator tree for text
print tree
if nextword != EOF :
error("there are extra words")
===================================================
This style of parsing is also called top-down parsing, predictive
parsing, and LL-parsing because it constructs the operator tree from the root
at the tree's top downwards towards the leaves, predicting the
correct structure by looking at the words in the input program,
one at a time. You can see how important it is to have exactly
the correct number of keywords and brackets at the exactly
correct positions in the input program so that this technique
will succeed. Parsing theory is the study of
how to write grammars and parsers successfully.
Once you have mastered writing parsers by hand, you realize that the process is almost completely mechanical --- starting from the grammar definition, you mechanically write the correct code. Now, you are ready to use a tool called a parser generator to do the code writing for you: The input to a parser generator is the set of grammar rules and the output is the parser. Yacc is a well known parser generator, and PLY is a version of Yacc coded to work with Python. Antlr is another popular parser generator.
Exercise: Copy the scanner and parser into one file and the command interpreter into another. In a third file, write a driver program that reads a source program and then imports and calls the scanner-parser and interpreter modules.
Exercise: Add an if-else command to the parser and interpreter.
Exercise: Add parameterless procedures to the language:
COMMAND ::= . . . | proc I : C | call I
In the interpreter, save the body of a newly defined procedure
in the namespace. (That is, the semantics of
proc I: C is similar to I = C.) What is the semantics of
call I? Implement this.
Someday, you will be asked to design a language of your own. Indeed, this happens each time you design a piece of software, because the inputs to the software must arrive in a sensible order --- syntax --- for the software to process them. Software used by humans requires an input language so that a human knows the rules (grammar) for communicating with the software. Sometimes, the grammar is just a matter of the order of mouse drags and clicks; this is a kind of point-and-shove language that a human might use to another human when the two people are unwilling to speak words to each other.
But when a human wishes to speak (type) words to a program, a real language of words, phrases, and sentences is required. What should this language look like? What operations, data, control are needed within it? When a GUI must map a sequence of mouse drags and clicks into target code, what kind of code should it generate? If you are designing a piece of software, you must design its input language, and you must write the parser and the interpreter for the language. This is why we must learn the technques in this chapter and this course.
Programming languages that are designed to solve problems in some specialty area (e.g., avionics, telecommunications, word processing, database access, game playing) must have operations that are tailored to the specialty area and must have data and control structures that support the forms of computation in the area. A language oriented towards a specialty area is called a domain-specific programming language. By the end of this course, you will have basic skills to design such languages.
By the way, grammar (BNF) notation is a domain-specific programming language --- for writing parser programs! There are automated systems (Yacc, PLY, Antlr, Bison, ...) that can read a grammar definition and automatically write the parser code that we wrote by hand in this chapter. So, when you write a grammar, you have, for all practical purposes, already written its parser --- what's left to do is purely mechanical.