Copyright © 2008 David Schmidt
Chapter 6:
The predicate-logic quantifiers
- 6.1 The universal quantifier and its deduction rules
- 6.1.1 Other ways of proving propositions with the universal quantifier
- 6.1.2 Application of the universal quantifier to programming functions
- 6.1.3 Application of the universal quantifier to data structures
- 6.2 The existential quantifier
- 6.2.1 Applications of the existential quantifier
- 6.2.2 The forwards assignment law uses an existential quantifier
- 6.3 The law for assigning to individual array elements
- 6.4 Case studies
- 6.4.1 In-place selection sort
- 6.4.2 Binary search
- 6.4.3 Maintaining a board game: programming by contract
- 6.5 Equivalences in predicate logic
- 6.6 Predicate logic without the existential quantifier: Skolem functions
- 6.7 Resolution theorem proving for predicate logic
- 6.8 Soundness and completeness of deduction rules
- 6.9 Summary
In the previous chapter, we studied how to combine primitive
propositions with the operators, ∧, ∨, —>, and ¬.
When we wrote propositions like
(p ∧ q) —> r, we pretended that p, q, and r
stood for complete, primitive statements like
``It is raining'' or ``x + 1 > 0''. We did not try to disassemble
p, q, and r.
Now it is time to decompose and analyze primitive
propositions in terms of their ``verbs'' (called predicates)
and their ``nouns'' (called individuals).
This leads to predicate logic.
First, some background: When we study a particular ``universe'' or
``domain'' consisting of ``individuals,'' we
make assertions (propositions) about the individuals in the domain.
Example domains are: the domain of all animals,
the domain of U.S. Presidents,
the domain of days-of-the-week,
the domain of crayon colors,
the domain of integers,
the domain of strings, etc.
We assemble propositions by using the individuals in the domain along
with some predicates.
For example, for the domain of integers, we use
predicates like == and >,
like this:
3 > 5, 2 * x == y + 1, etc. (Here, 3 and 5 are
individuals, and x and y are names of individuals.)
As these examples show,
we might also use functions, like * and +, to
compute new individuals.
For nonnumeric domains like humans, animals, and objects,
predicates are written in a function-call style, like this:
hasFourLegs(_), isTheMotherOf(_,_), isHuman(_), isOlderThan(_,_),
etc.
So, if Lassie is an individual animal, we write
hasFourLegs(Lassie) to make the proposition, ``Lassie has four legs.''
Another example is
isOlderThan(GeorgeWashington, AbrahamLincoln), which uses the
individuals GeorgeWashington and AbrahamLincoln.
Predicate logic has two important new operators that let us write stronger
propositions than what we can do with mere predicates.
These operators are called
quantifiers. The quantifers are ``for all'' (∀), and ''exists'' (∃).
In this chapter, we will
learn to use the quantifiers
to reason about data structures.
The ∀ quantifier helps us write propositions about all the
individuals in a domain. Say we consider the domain of animals.
The sentence,
``All humans are mortal'' is written like this:
-
∀x (isHuman(x) —> isMortal(x))
That is, if an individual, x, is human, then x is mortal also.
(Notice that dogs like Lassie are individuals in the domain,
but the above proposition cannot be used to show that Lassie is mortal,
since dogs aren't human. Sadly, dogs are nonetheless mortal.)
An arithmetic example looks like this: for the domain of ints,
``every value is less-than-or-equal to its square'':
-
∀n (n <= n * n)
A data-structure example looks like this:
For array, r, we can assert that every element of r is positive:
-
∀i ((i >= 0 ∧ i < len(r)) —> r[i] > 0)
That is, for every index int, i, in the range of 0 up to
(but not including) len(r) (the length of r), the indexed element
r[i] is greater than 0.
The previous statement is often written in a ``shorthand'' like this:
-
∀ 0 <= i < len(r), r[i] > 0
which we later use in many of our programming examples.
The ∃ quantifier helps us write propositions about specific
individuals in a domain, where the name of the individual is unimportant
or unknown.
For example, we can say that Lassie has a mother like this:
-
∃x isMotherOf(x, Lassie)
(''There exists some x such that x is the mother of Lassie.'')
Here is how we write that every individual in the domain has a mother:
-
∀x∃y isMotherOf(y, x)
For the domain of integers, we can make assertions like these:
∃x (x * x = x)
∃y (y + 2 = 9)
∀x (x > 1) —> (∃y (y > 0 and y + 1 = x))
For array r, we can say that r holds at least one negative int like this:
∃i (i >= 0 ∧ i < len(r) ∧ r[i] < 0)
(The shorthand version is ∃ 0 <= i < len(r), r[i] < 0.)
Lots more examples will follow.
With the new format of primitive propositions,
we can write proofs like before:
===================================================
isHuman(Socrates) —> isMortal(Socrates), isHuman(Socrates) |− isMortal(Socrates) ∧ isHuman(Socrates)
1. isHuman(Socrates) —> isMortal(Socrates) premise
2. isHuman(Socrates) premise
3. isMortal(Socrates) —>e 1,2
4. isMortal(Socrates) ∧ isHuman(Socrates) ∧i 3,2
===================================================
But more importantly, we will learn to prove claims like this:
∀x(isHuman(x) —> isMortal(x)), isHuman(Socrates) |− isMortal(Socrates)
6.1 The universal quantifier and its deduction rules
Like the other logical operators, ∀ has an introduction rule and
an elimination rule.
It works best to introduce the rules via examples.
First,
here is the most famous claim in logic:
- All humans are mortal.
- Socrates is human.
- Therefore, Socrates is mortal.
We express this
ancient claim like this:
∀x (isHuman(x) —> isMortal(x)), isHuman(Socrates) |− isMortal(Socrates)
Clearly, we require a kind of matching/binding rule to prove
that the human individual, Socrates, is mortal. The rule
is ∀e (``all elimination''):
===================================================
1. ∀x (isHuman(x) —> isMortal(x)) premise
2. isHuman(Socrates) premise
3. isHuman(Socrates) —> isMortal(Socrates) ∀e 1
4. isMortal(Socrates) —>e 3,2
===================================================
Line 3 shows that the claim on Line 1, which holds for all
individuals in the domain, can apply specifically
to Socrates, an individual member of the domain.
We use the new knowledge on Line 3 to reach the conclusion on Line 4.
∀e tailors a general claim, prefixed by ∀x,
to any individual element (who replaces the x).
We see this in Line 3 above. Here is the rule's schematic:
===================================================
∀x P_x
∀e: ------------
P_v that is, [v/x]P_x, where v is an individual in the domain
===================================================
(Here, P_x stands for a proposition that contains some occurrences of x.
Recall that [v/x]P_x is ``substitution notation'': substitute v for
occurrences of x in P_x.)
For example, from the premise,
∀i (i + 1 > i),
we apply ∀e to deduce [3/i](i + 1 > i), that is,
3 + 1 > 3.
The other deduction rule, ∀i (``all-introduction''),
deduces propositions that are prefixed by ∀.
Here is a motivating example, in the domain of integers:
∀n((n + 1) > n), ∀n(n > (n - 1)) |− ∀n((n + 1) > n ∧ n > (n - 1))
That is, we wish to prove that for every possible int, the int is smaller than
its successor and larger than its predecessor.
How do we do this?
Clearly, we will not inspect all of ..., -2, -1, 0, 1, 2, ...
and verify that
(-2 + 1) > -2 ∧ -2 < (-2 - 1),
(-1 + 1) > -1 ∧ -1 < (-1 - 1),
(0 + 1) > 0 ∧ 0 < (0 - 1), etc.!
Instead, we write a single, generic, general-purpose argument ---
a ``case analysis'' --- that applies to whichever, arbitrary int
we would ever consider. Let a stand for the arbitrary int we will discuss.
The case analysis appears in the proof like this:
===================================================
∀n ((n + 1) > n), ∀n (n > (n - 1)) |− ∀n ((n + 1) > n ∧ n > (n - 1))
1. ∀n ((n + 1) > n) premise
2. ∀n (n > (n - 1)) premise
... 3. a
... 4. (a + 1) > a ∀e 1
... 5. a > (a - 1) ∀e 2
... 6. (a + 1) > a ∧ a > (a - 1) ∧i 4,5
7. ∀n ((n + 1) > n ∧ n > (n - 1)) ∀i 3-6
===================================================
Lines 3-6 are the generic argument: let a be the arbitrary/anybody integer we
discuss. By Lines 1 and 2, we must have that (a + 1) > a
and that a > (a - 1). Line 6 uses ∧i to show a
has the property (a + 1) > a ∧ a > (a - 1).
Since the argument in Lines 3-6 is not
specific to any specific integer, we can use the
argument on all the individual integers --- that is,
we can substitute -2 for a and the argument holds; we can substitute
-1 for a and the argument holds;
we can substitute 0 for a and the argument holds;
and so on!
Line 7 is justified by the new deduction rule,
∀i, which asserts that the generic case analysis in Lines 3-6
applies to all the individual integers. Here is the rule's schematic:
===================================================
... a (a must be a brand new name)
... P_a
∀i: ------------
∀x P_x (That is, P_x is [x/a]P_a.
Thus, a _does not appear_ in P_x, and
every premise and assumption visible
to ∀x P_x _does not mention_ a)
===================================================
To repeat this important idea:
The rule says,
to prove a claim of form, ∀x P_x,
we undertake a case analysis:
we prove property P_a for an arbitrary member, a, of domain D.
(Call the element, ``Mister a'' --- Mister arbitrary --- Mister anybody --- Mister anonymous). Since Mister a
is a complete unknown, it stands for ``everyone'' in doman D.
We know that we can
substitute whichever domain element, d, from domain D we want
into the proof and we
get a proof of P_d. In this way, we have proofs of P
for all elements of domain D.
Here is the same idea, used in a proof about a domain of people:
''Everyone is healthy; everyone is happy. Therefore,
everyone is both healthy and happy'':
∀x isHealthy(x), ∀y isHappy(y) |− ∀z(isHealthy(z) ∧ isHappy(z))
===================================================
1. ∀x isHealthy(x) premise
2. ∀y isHappy(y) premise
... 3. a
... 4. isHealthy(a) ∀e 1
... 5. isHappy(a) ∀e 2
... 6. isHealthy(a) ∧ isHappy(a) ∧i 4,5
7. ∀z(isHealthy(z) ∧ isHappy(z)) ∀i 3-6
===================================================
Say that we have a domain of living beings.
This next example requires nested cases:
- All humans are mortal
- All mortals have soul
- Therefore, all humans have soul
===================================================
∀x (isHuman(x) —> isMortal(x)),
∀y (isMortal(y) —> hasSoul(y))
|− ∀x (isHuman(x) —> hasSoul(x))
1. ∀x (isHuman(x) —> isMortal(x)) premise
2. ∀y (isMortal(y) —> hasSoul(y)) premise
... 3. a
... ... 4. isHuman(a) assumption
... ... 5. isHuman(a) —> isMortal(a) ∀e 1
... ... 6. isMortal(a) —>e 4,3
... ... 7. isMortal(a) —> hasSoul(a) ∀e 2
... ... 8. hasSoul(a) —>e 6,5
... 9. isHuman(a) —> hasSoul(a) —>i 4-8
10. ∀x (isHuman(x) —> hasSoul(x)) ∀i 3-9
===================================================
Line 3 states that we use a to stand for an arbitrary individual of the
domain. Line 4 starts a nested case, which assumes
a is human. Then
we can prove that a has a soul, hence by —>i,
isHuman(a) —> hasSoul(a). Since the outer case is stated in
terms of the arbitrary, anonymous individual, a, we can finish the
proof on Line 10 by
∀i.
Here is a last, important example. Let the domain be the
members of one family.
We can prove this truism:
-
Every (individual) family member who is healthy is also happy.
-
Therefore, if all the family members are healthy, then all the members are happy.
===================================================
∀x (healthy(x) —> happy(x)) |− (∀y healthy(y)) —> (∀x happy(x))
1. ∀x healthy(x) —> happy(x) premise
... 2. ∀y healthy(y) assumption
... ... 3. a
... ... 4. healthy(a) ∀e 4
... ... 5. healthy(a) —> happy(a) ∀e 1
... ... 6. happy(a) —>e 5,4
... 7. ∀ x happy(x) ∀i 3-6
8. (∀y healthy(y)) —> (∀x happy(x)) —>i 2-7
===================================================
We commence by assuming all the family is
healthy (Line 2). Then, we consider an arbitrary/anonymous family
member, a, and show that healthy(a) is a fact (from Line 2).
Then we deduce happy(a). Since a stands for anyone/everyone
in the family, we use foralli to
conclude on Line 7 that all family members are happy. Line 8 finishes.
Consider the converse claim; is it valid?
-
If all the family members are healthy, then all are happy.
-
Therefore, for every (individual) family member, if (s)he is healthy then (s)he is also happy.
Well, no --- perhaps the family is so close-knit that, if one
one family member is unhealthy; then other, healthy,
family members might well be unhappy with worry.
This is a subtle point, so take a moment and think about it!
Let's try to prove the dubious claim and see where we get stuck:
===================================================
(∀y healthy(y)) —> (∀x happy(x)) |−
∀x (healthy(x) —> happy(x))
1. (∀y healthy(y)) —> (∀x happy(x)) premise
... 2. a assumption
... ... 3. healthy(a) assumption WE ARE TRYING TO PROVE happy(a)?!
4. ∀y healthy(y) ∀i 2-3?? NO --- WE ARE TRYING TO FINISH
THE OUTER BLOCK BEFORE THE INNER ONE IS FINISHED!
===================================================
No matter how you might try, you will see that the
``block structure'' of the proofs warns us when we
are making invalid deductions. It is impossible to prove this claim.
More examples
We state some
standard exercises with ∀,
where the domains and predicates are unimportant:
===================================================
∀x F(x) |− ∀y F(y)
1. ∀x F(x) premise
... 2. a
... 3. F(a) ∀e 1
4. ∀y F(y) ∀i 2-3
===================================================
===================================================
∀z (F(z) ∧ G(z) |− (∀x F(x)) ∧ (∀y G(y))
1. ∀z (F(z) ∧ G(z) premise
... 2. a
... 3. F(a) ∧ G(z) ∀e 1
... 4. F(a) ∧e1 3
5. ∀x F(x) ∀i 2-4
... 6. b
... 7. F(b) ∧ G(b) ∀e 1
... 8. G(b) ∧e2 7
9. ∀y F(y) ∀i 6-8
10. (∀x F(x)) ∧ (∀y G(y)) ∧i 5,9
===================================================
The earlier example about healthy and happy families illustrates an
important structural relationship between ∀ and —>:
∀x (F(x) —> G(x)) |− (∀x F(x)) —> (∀x G(x))
can be proved,
but the converse cannot.
This last one is reasonable but the proof is a bit tricky
because of the nested subproofs:
===================================================
∀x ∀y F(x,y) |− ∀y ∀x F(x,y)
1. ∀x ∀y F(x,y) premise
... 2. b
... ... 3. a
... ... 4. ∀y F(a,y) ∀e 1
... ... 5. F(a,b) ∀e 4
... 6. ∀x F(x,y) ∀i 3-5
7. ∀y ∀x F(x,y) ∀i 2-6
===================================================
Tactics for the ∀-rules
As in the previous chapter, we now give advice as to when to use
the ∀i and ∀e rules.
(***) ∀i-tactic: To prove Premises |− ∀x P_x,
-
assume a, for a new, anonymous ``Mister a''
-
prove Premises |− P_a
-
finish with ∀i.
The proof structure looks like this:
1. Premises premise
... i. a
(fill in)
... j. P_a
k. ∀x P_x ∀i i-j
This tactic was applied in Lines 2-7 of the previous (correct) example proof.
-
(*) ∀e-tactic: To prove Premises, ∀x P_x |− Q,
then for an individual, i, that appears
in the proof so far, use the ∀e rule to deduce the new fact,
P_i:
1. Premises premise
2. ∀x P_x premise
. . .
j. P_i ∀e 2
(fill in)
k. Q
This tactic should be used only when it is clear that the new
fact makes a significant step forwards to finishing the proof.
Steps 4 and 5 of the previous (correct) example proof used this tactic.
6.1.1 Other ways of proving propositions with the universal quantifier
How do we prove an assertion of the form, ∀x P_x?
We just saw that ∀i can do this for any domain whatsoever.
But there are, in fact, three different approaches, depending on
the form of domain we use:
Approach 1: use conjunctions for a finite domain
-
Say that the domain we study is a finite set,
D = {e0, e1, ..., ek}.
(An example domain is the days of the week,
{sun, mon, tues, weds, thurs, fri, sat}.)
This makes
∀x P_x just an abbreviation itself of this much-longer assertion:
P_e0 ∧ P_e1 ∧ ... ∧ P_ek
For example, when the domain is the days of the week, the assertion,
∀d isBurgerKingDay(d), abbreviates
isBurgerKingDay(sun) ∧ isBurgerKingDay(mon) ∧ isBurgerKingDay(tues) ∧ ... ∧ isBurgerKingDay(sat)
To prove such a ∀x P_x for a finite domain D, we
must prove P_ei, for each and every ei in D.
We can use this approach when we are analyzing all the elements of
a finite-length array. Say that array r has length 4.
We can say that the domain of its indexes is {0, 1, 2, 3}.
So, if we wish to prove that ∀ 0 <= i < 4, r[i] > 0,
we need only prove that
r[0] > 0 ∧ r[1] > 0 ∧ r[2] > 0 ∧ r[3] > 0.
-
Approach 2: for the domain of nonnegative ints, use mathematical induction
-
The domain, Nat = {0, 1, 2, ... } is infinite, so we
cannot use the previous technique to prove properties like
∀ n > 0, (n + 1) > n --- we would have to write separate proofs
that 0 + 1 > 0, 1 + 1 > 1, 2 + 1 > 2, ..., forever.
But we can use mathematical induction. Remember how it
works: we write two proofs:
-
basis case:
a proof of P_0
-
induction case:
a proof of
P_k —> P_k+1, where k is a brand new variable name
(At this point, it would be a very good idea for you to review Section 4.5
of the Lecture Notes, Chpater 4.)
There is a variation of mathematical induction that we use
when proving loop invariants of the form,
∀ 0 <= k < count, P_k:
...
count = 0
{ (a) ∀ 0 <= k < count, P_k }
while B
{ (b) invariant ∀ 0 <= k < count, P_k }
...
{ retain: ∀ 0 <= k < count, P_k
prove: P_k
implies: ∀ 0 <= k < count + 1, P_k }
count = count + 1
{ (c) ∀ 0 <= k < count, P_k }
-
We start with this assertion, at point (a):
∀ 0 <= k < 0, P_k
This assertion is true because it defines an empty range of integers ---
there are
no elements in the
domain defined by {k:int | 0 <= k ∧ k < 0}.
Hence, for all the elements, k, in the empty domain, we have
proved P_k(!)
This proves the Basis case.
-
Using the loop invariant (the induction hypothesis), starting
at point (b),
we analyze the loop's body and prove
P_count
That is, P holds for the value, count.
Using ∧i we get
∀ 0 <= k < count, P_k ∧ P_count
This can be understood as
(P_0 ∧ P_1 ∧ P_2 ∧ ... ∧ P_count-1) ∧ P_count
Based on what we read in Approach 1 earlier,
we combine the facts into this one:
∀ 0 <= k < count + 1, P_k
Since the loop's body ends with the assignment,
count = count + 1,
we recover the loop invariant at point (c).
This is the proof of the induction case.
We will see several uses of this approach in the next Section.
Approach 3: for any domain, finite or infinite whatsoever,
use the ∀i-law
-
Finally, we might be using a large domain that is not as organized as
the nonnegatives, 0,1,2,.... Maybe the domain is the domain
of all humans or all the citizens of Peru or
or the members of the Republican party or
all the objects on Planet Earth. How can we prove
∀ x P_x for such huge collections?
To prove a claim of form, ∀x P_x,
for an arbitrary domain,
we undertake a kind of case analysis:
we prove property P_a for an arbitrary member, a, of domain D.
(Call the element, ``Mister a'' --- Mister arbitrary --- Mister anybody --- Mister anonymous). Since Mister a
is a complete unknown, it stands for ``everyone'' in doman D.
We know that we can
substitute whichever domain element, d from domain D, we want
into the proof and we
get a proof of P_d. In this way, we have proofs of P
for all elements of domain D.
This is the idea behind the ∀i-rule.
6.1.2 Application of the universal quantifier to programming functions
We have been using the rules for the universal quantifier every time we
call a function. A function's parameter names are like the variables
x and y in ∀x and ∀y.
Here is an example:
===================================================
def fac(n) :
{ pre n >= 0
post ans == n!
return ans
}
===================================================
We saw in the previous chapter that the pre- and post-condition
can be combined into this compound proposition,
(n >= 0) —> (fac(n) == n!)
which describes fac's behavior in terms of name n.
But n is a parameter name that is internal to fac's code.
A more proper specification, one that makes sense to fac's caller, is
∀n ((n >= 0) —> (fac(n) == n!))
That is, ``for all possible int arguments, if the argument is nonnegative, then
fac computes the argument's factorial.''
We use this logical propery when we call the function.
Here is the proof of it:
===================================================
x = fac(6)
{ 1. ∀n((n >= 0) —> (fac(n) == n!)) premise (about fac )
2. 6 >= 0 algebra
3. (6 >= 0) —> (fac(6) == 6!) ∀e 1
4. fac(6) == 6! —>e 3,2
5. x == fac(6) premise (the assign law)
6. x == 6! subst 4,5
}
===================================================
∀e applies the function's logical property to its argument.
The function-call law we learned in Chapter 3 hid the ∀ ---
we weren't ready for it yet! But the universal quantifier is
implicit in the description of every function we call.
When we wrote the coding of fac, we also built a proof that
fac computes and returns n!, for input parameter name, n.
We didn't know if n will equal
1 or 9 or 99999 --- we just call it n and work with the
name. This is just a ``Mr. anybody'', exactly
as we have been using in our case analyses that finish with ∀i.
The rule for function building hides the use of ∀i ---
we were not ready for it in Chapter 3. But writing a
function is the same thing as writing a proof that
finishes with ∀i.
6.1.3 Application of the universal quantifier to data structures
A data structure is a container for holding elements from a domain,
and we often use universal quantifiers to write assertions about the data
structure and how to compute upon it. We use the ∀i and ∀e
rules to reason about the elements that are inserted and removed from
the data structure.
We use arrays (lists) in the examples in this chapter.
First, recall these Python operators for arrays:
-
For array r, r.append(e) adds element e to the end of
r:
===================================================
a = [2, 3, 5, 7]
print a # prints [2, 3, 5, 7]
a.append(11)
print a # prints [2, 3, 5, 7, 11]
===================================================
-
For array r,
r[:index] computes a new array that is the ``slice'' of r
up to and not including r[index]:
===================================================
c = [2, 3, 5, 7, 11, 13, 17, 19]
e = c[:6]
print e # prints [2, 3, 5, 7, 11, 13]
f = c[:0]
print f # prints []
print c # prints [2, 3, 5, 7, 11, 13, 17, 19]
===================================================
-
For array, r,
r[index;] computes a new array that is the ``slice'' of r
from r[index] to the end of r:
===================================================
c = [2, 3, 5, 7, 11, 13, 17, 19]
g = c[4:]
print g # prints [11, 13, 17, 19]
h = c[:8]
print h # prints []
print c # prints [2, 3, 5, 7, 11, 13, 17, 19]
===================================================
Here is an example; it is math-induction-like
(``Approach 2'' mentioned earlier). We outline below
how a procedure resets all the elements of an
array (list) to zeros:
===================================================
def zeroOut(a) :
{ pre isIntArray(a)
post ∀ 0 <= i < len(a), a[i] == 0
}
j = 0
while j != len(a) :
{ invariant ∀ 0 <= i < j, a[i] == 0 }
a[j] = 0
{ assert ∀ 0 <= i < j, a[i] == 0 ∧ a[j] = 0
therefore, ∀ 0 <= i < j+1, a[i] == 0 (*) }
j = j + 1
{ assert ∀ 0 <= i < j, a[i] == 0 }
#END LOOP
{ assert j == len(a) ∧ (∀ 0 <= i < len(a), a[i] == 0)
therefore, ∀ 0 <= i < len(a), a[i] == 0 }
===================================================
We state that the range of elements from 0 up to (and not
including) j are reset to 0 by stating
∀ 0 <= i < j, a[i] == 0
This loop invariant leads to the goal as j counts through the range
of 0 up to the length of array a.
At the point marked (*), there is an informal
use of ∀i.
Here is a second, similar example:
===================================================
def doubleArray(a) :
"""doubleArray builds a new array that holds array a's values *2"""
{ pre: isIntArray(a)
post: isIntArray(answer) ∧ len(answer) == len(a)
∧ ∀ 0 <= i < len(a), answer[i] == 2 * a[i] }
index = 0
answer = []
while index != len(a) :
{ invariant isIntArray(answer) ∧ len(answer) == index ∧
∀ 0 <= i < index, answer[i] == 2 * a[i] }
{ assert: index != len(a) ∧ invariant }
answer.append([a[index]*2)
{ assert: invariant ∧ answer[index] == 2 * a[index]
implies: ∀ 0 <= i < index+1, answer[i] == 2 * a[i] } # (see Approach 2)
index = index + 1
{ assert: invariant }
{ assert: index == len(a) ∧ invariant
implies: isIntArray(answer) ∧ len(answer) == len(a)
implies: ∀ 0 <= i < len(a), answer[i] == 2 * a[i] }
return answer
===================================================
Notice how the postcondition notes that the answer array is the
same length as the parameter array. This prevents the function's code
from misbehaving and adding junk to the end of the answer array.
See the Case Studies for more examples.
6.2 The existential quantifier
The existential quantifier, ∃, means ``there exists'' or
``there is''.
We use this phrase when we do not care about the name of the individual
involved in our claim. Here are examples:
There is a mouse in the house: ∃m (isMouse(m) ∧ inHouse(m))
(We don't care about the mouse's name.)
Someone ate my cookie: ∃x ateMyCookie(x)
There is a number that equals its own square: ∃n n == n*n
For every int, there is an int that is smaller: ∀x ∃y y < x
If we have a fact about an individual in a domain, we can use
the fact to deduce a fact that begins with an existential quantifier.
For example, if we know that
isHuman(Socrates) ∧ isMortal(Socrates)
surely we can conclude that
∃h (isHuman(h) ∧ isMortal(h))
that is, ``there is someone who is human and mortal.''
The identity of the human is no longer important to us.
In the next section, we see that the ∃i-rule makes such deductions.
The existential-introduction rule
Often ∃ is used to ``hide'' secret information.
Consider these Pat Sajack musings from
a typical game of Wheel of Fortune:
-
Pat thinks:
``There is an 'E' covered over on Square 14 of the game board.''
In predicate logic, this can be written
isCovered(Square14) ∧ holds(Square14,'E').
-
Pat thinks: ''Wait --- I can't say that on TV! Perhaps I can say,
There is a vowel covered on Square 14 of the game board.''
In predicate logic, this is written
isCovered(Square14) ∧ (∃c isVowel(c) ∧ holds(Square14,c)).
In this way, Pat does not reveal the letter to the game players and TV
viewers.
-
Because it isn't fair to tell the players which squares hold vowels,
Pat announces on the air,
``There is a vowel that is still covered on the game board'':
∃s (isSquare(s) ∧ isCovered(s) ∧ (∃c isVowel(c) ∧ holds(s,c)))
This statement hides the specific square and letter that Pat is thinking about.
Pat's announcement was deduced
from its predecessors by means of
the
∃i-rule, which we see in a moment.
What can a game player do with Pat's uttered statement?
A player might
deduce these useful facts:
-
There is a square still covered:
∃s isSquare(s) ∧ isCovered(s)
-
There is a vowel:
∃c isVowel(c)
-
There is a covered letter, A, E, I, O, U (assuming
the vowels are exactly A, E, I, O, U):
∃s isSquare(s) ∧ isCovered(s) ∧
(holds(s,'A') ∨ holds(s,'E') ∨ holds(s,'I') ∨ holds(s,'O') ∨ holds(s,'U'))
Although the game player does not know the letter and square that
Pat Sajak ``hid'' with his statement, the player can still make
useful deductions.
We will use the ∃e rule to deduce these style of
propositions.
∃-introduction rule
The rule for ∃i has this format:
P_d where d is an individual in the domain D
∃i: ------------
∃x P_x
The ∃i rule says, if we locate an individual d (a ``witness'',
as it is called by logicians) that makes P true, then surely we can
say there exists someone
that has P and hide the identity of the individual/witness.
The rule was used in the previous section in a tiny example:
===================================================
isHuman(Socrates), isMortal(Socrates) |− ∃h (isHuman(h) ∧ isMortal(h))
1. isHuman(Socrates) premise
2. isMortal(Socrates) premise
3. isHuman(Socrates) ∧ isMortal(Socrates) ∧i 1,2
4. ∃h (isHuman(h) ∧ isMortal(h)) ∃i 3
===================================================
Since Socrates is an individual that is both human and mortal,
we deduce Line 3. Line 4 ``hides'' Socrates's name.
Let's do a Wheel-Of-Fortune example: Pat Sajak uses two premises
and the ∃i rule to deduce a new conclusion:
===================================================
isVowel('E'), holds(Square14,'E') |− ∃c(isVowel(c) ∧ ∃s holds(s,c))
1. isVowel('E') premise
2. holds(Square14,'E') premise
3. ∃s holds(s,'E') ∃i 2
4. isVowel('E') ∧ ∃s holds(s,'E') ∧i 1,3
5. ∃c(isVowel(c) ∧ ∃s holds(s,c)) ∃i 4
===================================================
Line 3 hides the number of the square (``there is a square that holds 'E' ''),
and Line 5 hides the 'E' (``there is a letter that is a vowel and there
is a square that holds the letter'').
From the same two premises
we can also prove this:
===================================================
1. isVowel('E') premise
2. holds(Square14,'E') premise
3. isVowel('E') ∧ holds(Square14,'E') ∧i 1,3
4. ∃s(isVowel('E') ∧ holds(s,'E')) ∃i 3
5. ∃c∃s(isVowel(s) ∧ holds(s,c)) ∃i 4
===================================================
This reads, ``there are a letter and square such that the letter is a
vowel and the square holds the letter.''
The proposition differs slightly from the previous one, but the two
seem to have identical information content. (When we learn the
∃e-rule, we can prove the two conclusions have identical content.)
The ∃-elimination rule
Since the ∃i-rule constructs propositions that begin with
∃, the ∃e-rule disassembles propositions that begin with
∃. The new rule employs a subtle case analysis.
Here is a quick example (in the universe of things on planet Earth), to get our bearings:
All humans are mortal
Someone is human
Therefore, someone is mortal
We don't know the name of the individual human, but it does not matter ---
we can still conclude someone is mortal. The steps we will take go like
this:
-
Since ``someone is human'' and since we don't know his/her name,
we'll just make up our own name for them --- ``Mister A''.
So, we assume that ``Mr. A is human''.
-
We use the logic rules we already know to prove that ''Mr. A is mortal''.
-
therefore ''someone is mortal'' and their name does not matter.
This approach is coded into the last logic law, ∃e
(exists-elimination):
Say we have a premise of the form,
∃x P_x. Since we do not know the name of the individual
``hidden'' behind the ∃x, we make up a name for it, say a, and
discuss what must follow from the assumption that P_a holds true:
... a P_a assumption (where a is a new, fresh name)
∃x P_x ... Q
∃e: ----------------------- (a MUST NOT appear in Q)
Q
That is, if we can deduce Q from P_a, and we do not mention
a within Q, then it means Q can be deduced no matter what
name the hidden individual has. So, Q follows from
∃x P_x.
We can work the previous example, with ∃e:
All humans are mortal
Someone is human
Therefore, someone is mortal
We make up the name, a, for the individual whose
name we do not know, and do a case analysis:
===================================================
∀h(isHuman(h) —> isMortal(h)), ∃x isHuman(x) |− ∃y isMortal(y)
1. ∀h(isHuman(h) —> isMortal(h)) premise
2. ∃x isHuman(x) premise
... 3. a isHuman(a) assumption
... 4. isHuman(a) —> isMortal(a) ∀e 1
... 5. isMortal(a) —>e 4,3
... 6. ∃y isMortal(y) ∃i 5
7. ∃y isMortal(y) ∃e 2, 3-6
===================================================
Line 3 proposes the name a and the assumption that isHuman(a).
The case analysis leads to Line 6, which says that
someone is mortal. (We never learned the individual's name!)
Since Line 6 does not explicitly mention the made-up name, a,
we use Line 7 to repeat Line 6 --- without knowing the name
of the individual ``hiding'' inside Line 2, we made a case analysis
in Lines 3-6 that prove the result, anyway. This is how ∃e works.
To repeat:
The ∃e rule describes how to discuss an anonymous individual
(a witness) without knowing/revealing its identity:
Assume the witness's name is Mister a (``Mister Anonymous'')
and that Mister a makes
P true. Then, we deduce some fact, Q, that holds even though
we don't know who is Mister a. The restriction on the
∃e rule (Q cannot mention a) enforces
that we have no extra information about
the identity of Mister a ---
the name a must not leave the subproof.
Here is a Wheel-of-Fortune example that uses ∃e:
===================================================
∃c (isVowel(c) ∧ ∃s holds(s,c)) |− ∃y isVowel(y)
1. ∃c (isVowel(c) ∧ ∃s holds(s,c)) premise
... 2. a isVowel(a) ∧ ∃s holds(s,a) assumption
... 3. isVowel(a) ∧e1 2
... 4. ∃y isVowel(y) ∃i 3
5. ∃y ∃y isVowel(y) ∃e 1,2-4
===================================================
We do not know the identity of the vowel held in an unknown
square, but this does not prevent us from concluding
that there is a vowel.
Standard examples
For practice, we do some standard examples:
===================================================
∃x P(x) |− ∃y P(y)
1. ∃x P(x) premise
... 2. a P(a) assumption
... 3. ∃y P(y) ∃i 2
4. ∃y P(y) ∃e 1,2-3
===================================================
===================================================
∃x(F(x) ∧ G(x)) |− (∃y F(y)) ∧ (∃z G(z))
1. ∃x(F(x) ∧ G(x)) premise
... 2. a F(a) ∧ G(a) assumption
... 3. F(a) ∧e1 2
... 4. ∃y F(y) ∃i 3
... 5. G(a) ∧e2 2
... 6. ∃z G(z) ∃i 5
... 7. (∃y F(y)) ∧ (∃z G(z)) ∧i 4,6
8. (∃y F(y)) ∧ (∃z G(z)) ∃e 1, 2-7
===================================================
Notice that you cannot prove the converse:
(∃y F(y)) ∧ (∃z G(z)) |− ∃x(F(x) ∧ G(x)).
For example, say that the universe of discussion is the cast of
Wheel of Fortune, and F == isMale and G == isFemale.
Clearly, Pat Sajak is male and Vanna White is female, so
(∃y F(y)) ∧ (∃z G(z)) is a true premise.
But ∃x(F(x) ∧ G(x)) does not follow.
The following proof uses the ∨e-tactic --- a cases analysis. See the assumptions
at lines 3 and 6, based on Line 2:
===================================================
∃x (P(x) ∨ Q(x)) |− (∃x P(x)) ∨ (∃x Q(x))
1. ∃x (P(x) ∨ Q(x)) premise
... 2. a P(a) ∨ Q(a) assumption
... ... 3. P(a) assumption
... ... 4. ∃x P(x) ∃i 3
... ... 5. (∃x P(x)) ∨ (∃x Q(x)) ∨i1 4
... ... 6. Q(a) assumption
... ... 7. ∃x Q(x) ∃i 6
... ... 8. (∃x P(x)) ∨ (∃x Q(x)) ∨i2 7
... 9. (∃x P(x)) ∨ (∃x Q(x)) ∨e 2,3-5,6-8
11. (∃x P(x)) ∨ (∃x Q(x)) ∃e 1,2-9
===================================================
As an exercise, prove the converse of the above:
(∃x P(x)) ∨ (∃x Q(x)) |− ∃x (P(x) ∨ Q(x)).
An important example
We finish with this crucial example.
We use the domain of people:
∃x ∀y isBossOf(x,y)
Read this as, ``there is someone who is the boss of everyone.''
From this strong fact we can prove that everyone has a boss, that is,
∀u∃v isBossOf(v,u):
===================================================
∃x∀y isBossOf(x,y) |− ∀u∃v isBossOf(v,u)
1. ∃x∀y isBossOf(x,y) premise
... 2. b ∀y isBossOf(b,y) assumption
... ... 3. a
... ... 4. isBossOf(b,a) ∀e 2
... ... 5. ∃v isBossOf(v,a) ∃i 4
... 6. ∀u∃v isBossOf(v,u) ∀i 3-5
7. ∀u∃v bossOf(v,u) ∃e 1,3-5
===================================================
In the above proof, we let b be our made-up name for the boss-of-everyone.
So, we have the assumption that ∀y isBossOf(b,y).
Next, we let a be ``anybody at all'' who we might examine in the domain of people.
The proof exposes that the boss of ``anybody at all'' in the domain must always
be b. ∀i and then ∃i finish the proof.
Here is the proof worked again, with the subproofs swapped:
===================================================
∃x∀y isBossOf(x,y) |− ∀u∃v isBossOf(v,u)
1. ∃x∀y isBossOf(x,y) premise
... 2. a
... ... 3. b ∀y isBossOf(b,y) assumption
... ... 4. isBossOf(b,a) ∀e 3
... ... 5. ∃v isBossOf(v,a) ∃i 4
... 6. ∃v bossOf(v,a) ∃e 1,3-5
7. ∀u∃v isBossOf(v,u) ∀i 2-6
===================================================
Can we prove the converse? That is, if everyone has a boss, then
there is one boss who is the boss of everyone?
∀u∃v isBossOf(v,u) |− ∃x∀y isBossOf(x,y) ???
No --- we can try, but we get stuck:
===================================================
1. ∀u∃v isBossOf(v,u) premise
... 2. a
... 3. ∃v isBossOf(v,a) ∀e 1
... ... 4. b isBossOf(b,a) assumption
5. ∀y isBoss(b,y) ∀i 2-5 NO --- THIS PROOF IS TRYING TO FINISH
THE OUTER SUBPROOF WITHOUT FINISHING THE INNER ONE FIRST.
===================================================
We see that the ``block structure'' of the proofs warns us when we
are making invalid deductions.
It is interesting that we can prove the following:
∃x∀y isBossOf(x,y) |− ∃z isBossOf(z,z)
(``if someone is the boss of everyone, then someone is their own boss'')
===================================================
∃x∀y isBossOf(x,y) |− ∀u∃v isBossOf(v,u)
1. ∃x∀y isBossOf(x,y) premise
... 2. b ∀y isBossOf(b,y) assumption
... 3. isBossOf(b,b) ∀e 2
... 4. ∃z isBossOf(z,z) ∃i 4
5. ∃z bossOf(z,z) ∃e 1,2-4
===================================================
Line 3 exposes that the ``big boss,'' b, must
be its own boss.
Domains and models
The examples of bosses and workers illustrate these points:
-
You must state the domain of individuals when you state
premises. In the bosses-workers examples, the domain is
a collection of people. Both the bosses and the workers belong
to that domain. Here are three drawings of possible different domains,
where an arrow, person1 ---> person2, means that person1 is the
boss of person2:
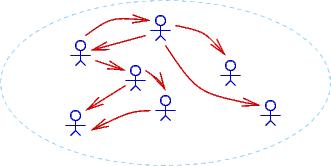
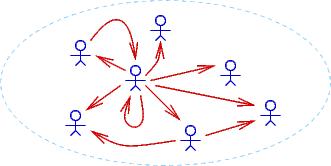
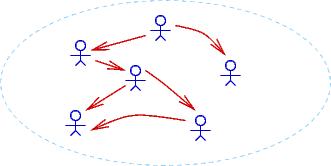
Notice that ∀u∃v isBossOf(v,u) (``everyone has a boss'')
holds true for the first two domains but not the third.
∃x∀y isBossOf(x,y) holds true for only the
second domain.
-
When we make a proof of P |− Q and P holds true for a domain,
then Q must also hold true for that same domain..
We proved that
∃x∀y isBossOf(x,y) |− ∃z isBossOf(z,z),
and sure enough, in the second example domain,
∃z isBossOf(z,z) holds true.
Our logic system is designed to work in this way! When we do a
logic proof, we are generating new facts that must hold true for
any domain for which the premises hold true. This property
is
called soundness of the logic, and we will examine it
more closely in a later section in this chapter.
-
A domain can have infinitely many individuals.
Here is a drawing of a domain of infinitely many people,
where each person bosses the person to their right:
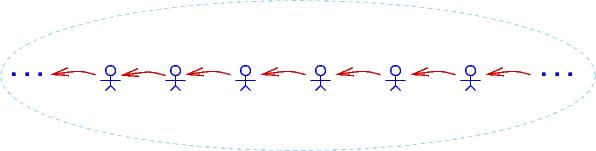
In this domain, ∀u∃v isBossOf(v,u) holds true
as does ∀u∃v isBossOf(u,v) (``everyone bosses someone''),
but ∃z isBossOf(z,z) does not hold true.
The third example domain is famous --- it is just the integer domain,
where isBossOf is actually >:
. . . < -3 < -2 < -1 < 0 < 1 < 2 < 3 < . . .
Indeed, one of the main applications of logic is proving properties
of numbers. This leads to a famous question: Is it possible to
write a collection of premises from which we can deduce (make proofs of)
all the logical properties that hold true for the domain of integers?
The answer is NO. In the 1920s, Kurt Goedel, a German PhD student,
proved that the integers, along with +, -, *, /, are so complex that
it is impossible to ever formulate a finite set (or even an algorithmically
defined infinite set) of premises that generate all the true properties
of the integers. Goedel's result, known as the First Incompleteness Theorem,
set mathematics back on its heels and directly led to the formulation
of theoretical computer science (of which this course is one small part).
There is more material about Goedel's work at the end of this chapter.
Tactics for the ∃-rules
There are two tactics; neither is easy to master:
-
(***) ∃e-tactic: To prove Premises, ∃x P_x |− Q,
-
assume a and P_a, where a is a brand new anonymous name
-
prove Premises, P_a |− Q
-
apply ∃e
The proof looks like this:
1. Premises premise
2. ∃x P_x premise
... i. a P_a assumption
(fill in)
... j. Q (does not mention a!)
k. Q ∃e 2,i-j
-
(*) ∃i-tactic: To prove Premises |− ∃x P_x,
try to prove P_e for some e that already appears in the partially
completed proof. Finish with ∃i:
1. Premises premise
. . .
i. ...e...
(fill in)
j. P_e
k. ∃x P_x ∃i j
Look at the Wheel-of-Fortune proofs for instances where these
tactics were applied.
6.2.1 Applications of the existential quantifier
Since an existential quantifier hides knowledge, it is useful to describe
a function that returns some but not all the information that the
function computes. Here is a simple example, for a computerized
Wheel-of-Fortune game:
===================================================
board = ... { invariant: isStringArray(board) ∧ len(board) > 0 }
def gameOver() :
"""examines board to see if all squares uncovered. Returns True if so,
otherwise returns False."""
{ gameOver_pre true }
{ gameOver_post answer —> ¬(∃ 0 <= i < len(board), board[i] == "covered")
∧ ¬answer —> (∃ 0 <= i < len(board), board[i] == "covered")
}
answer = True
... while loop that searches board for a board[k] == "covered";
if it finds one, it resets answer = False ...
return answer
===================================================
The computerized Pat Sajak would use this function like this:
===================================================
done = gameOver()
if done :
print "We have a winner! Time for a commercial!"
else :
print "There is still a letter that is covered. Let's continue!"
===================================================
Here is the relevant deduction:
===================================================
done = gameOver()
{ assert: [done/answer]gameOver_post }
if done :
{ 1. done premise
2. [done/answer]gameOver_post premise
3. done —> ¬(∃ 0 < i < len(board), board[i] == "covered") ∧e 2
4. ¬(∃ 0 < i < len(board), board[i] == "covered") —>e 3,1 }
print "We have a winner! Time for a commercial!"
else :
{ 1. ¬done premise
2. [done/answer]gameOver_post premise
3. ¬done —> (∃ 0 < i < len(board), board[i] == "covered") ∧e 2
4. ∃ 0 < i < len(board), board[i] == "covered" —>e 3,1 }
print "There is still a letter that is covered. Let's continue!"
===================================================
Notice that the answer returned by gameOver hides which square on the
board is still covered (== "covered").
We repeat an example from a previous chapter to show another use
of the existential:
===================================================
def delete(c, s) :
"""delete locates an occurrence of c in s and
removes it and returns the resulting string.
If c is not in s, a copy of s is returned, unchanged.
"""
{ pre: isChar(c) ∧ isString(s) }
{ post: (∃ 0 <= k < len(s), s[k] == c ∧ answer == s[:k] + s[k+1:])
∨
(∀ 0 <= i < len(s), s[i] != c) ∧ answer == s }
index = 0
found = False
while index != len(s) and not found :
{ invariant (∀ 0 <= i < index, s[i] != c) ∧
(found —> s[index] == c) }
if s[index] == c :
found = True
else :
index = index + 1
{ assert: (index == len(s) ∨ found) ∧ above invariant }
if found :
answer = s[:index] + s[index+1:]
{ 1. found premise
2. answer == s[:index] + s[index+1:] premise
3. invariant premise
4. (found —> s[index] == c) ∧e 3
5. s[index] == c —>e 4,1
6. s[index] == c ∧ answer == s[:index] + s[index+1:] ∧i 5,2
7. 0 <= index < len(s) algebra 5
8. ∃ 0 <= k < len(s), s[k] == c ∧ answer == s[:k] + s[k+1:] ∃i 7,6 (where [k/index])
}
else :
answer = s
{ 1. ¬found premise
2. answer == s premise
3. (index == len(s) ∨ found) premise
4. invariant premise
5. index == len(s) by P ∨ Q, ¬Q |− P, 3,1
6. ∀ 0 <= i < index, s[i] != c ∧e 4
7. ∀ 0 <= i < len(s), s[i] != c substitution 5,6
8. (∀ 0 <= i < len(s), s[i] != c) ∧ answer == s ∧i 7,2
}
return answer
===================================================
The ∃i rule is used inside the then-arm of the last conditional,
as shown above.
It is important that delete hide the value
of its local variable, index, from appearing in its postcondition,
because we do not want confusion like this:
===================================================
index = 2
t = "abcd"
u = delete("a", t)
{ at this point, we certainly cannot assert that t[2] = "a"! }
===================================================
6.2.2 The forwards assignment law uses an existential quantifier
The original, proper statement of the forwards assignment law reads like this:
{ assert: P }
x = e
{ assert: ∃x_old ( (x == [x_old/x]e) ∧ [x_old/x]P ) }
Our use of x_old was hiding the quantifier.
Using ∃, we can retain an assertion that uses the old value
of x.
In the earlier chapters, we worked examples like this:
===================================================
{ x > 0 }
x = x + 1
{ 1. x_old > 0 premise
2. x == x_old + 1 premise
3. x > 1 algebra 1,2
}
===================================================
and noted that x_old must not appear in the last line of the proof.
The above proof is actually the subproof of a proof that finishes
with ∃e! Here is the proper proof:
===================================================
{ x > 0 }
x = x + 1
{ 1. ∃x_old(x_old > 0 ∧ x == x_old + 1) premise
... 2. x_old x_old > 0 ∧ x == x_old + 1 assumption
... 3. x_old > 0 ∧e1 2
... 4. x == x_old + 1 ∧e2 2
... 5. x > 1 algebra 3,4
6. x > 1 ∃e 1, 2-5
}
===================================================
Again, it is crucial that x_old not appear in the assertions on Lines
5 and 6.
We unconsciously use the existential quantifier and ∃e every time
we reason about the old, overwritten value of an updated variable.
Also,
when we introduce dummy names, like x_in and
y_in, to stand for specific values, as an example like this,
===================================================
{ assert: x == x_in ∧ y == y_in }
temp = x
x = y
y = temp
{ assert: x == y_in ∧ y == x_in }
===================================================
we are implicitly using existential quantifiers, again, like this:
===================================================
{ assert: ∃x_in ∃y_in(x == x_in ∧ y == y_in) }
temp = x
x = y
y = temp
{ assert: ∃x_in∃y_in(x == y_in ∧ y == x_in) }
===================================================
6.3 The law for assigning to individual array elements
A key property of the forwards law for an assignment, x = e, is that
the ``old'' value of x cannot appear in the final consequence that
is deduced from the assignment.
The same principle holds for assignment to an individual
array element: a[e] = e' --- the ``old'' value of a[e] cannot
appear in the assertion that
results from the assignment.
For example,
if we have
{ assert: len(a) > 0 ∧ ∀ 0 <= i < len(a), a[i] > 0 }
a[0] = 0
we should be able to deduce that
{ assert: a[0] == 0
∧ len(a) > 0
∧ ∀ 0 < i < len(a), a[i] > 0
implies: ∀ 0 <= i < len(a), a[i] >= 0 }
How can we do this? The existing assignment law is too weak.
We require a special law for assignment to array elements.
The situation gets delicate if we are
unable to deduce the precise numerical value of the index
expression, e, in an assignment,
a[e] = e'.
Unless we can prove otherwise,
the assignment has essentially updated ``all'' of a!
Here is an example of a situation where we know nothing about
which cell was updated:
===================================================
n = readInt("Type an int between 0 and len(a)-1: ")
assert 0 <= n and n < len(a)
a[n] = a[n] - 1
===================================================
Clearly only one element of
a is decremented.
Let's try to reason about this situation:
===================================================
{ assert: ∀ 0 <= i < len(a), a[i] > 0 }
n = readInt("Type an int between 0 and len(a)-1: ")
assert 0 <= n and n < len(a)
{ assert: 0 <= n ∧ n < len(a) ∧ ∀ 0 <= i < len(a), a[i] > 0 }
a[n] = a[n] - 1
{ assert: a[n] == a_old[n] - 1 ∧ 0 <= n ∧ n < len(a)
∧ ∀ 0 <= i < len(a), a_old[i] > 0
implies: ???
}
===================================================
To move forwards, we must assert that all those variables a[i], such
that i != n, retain their old values:
===================================================
a[n] = a[n] - 1
{ 1. a[n] == a_old[n] - 1 premise
2. ∀ 0 <= i < len(a), (i!=n) —> a[i] == a_old[i] premise NEW!
3. 0 <= n ∧ n < len(a) premise
4. ∀ 0 <= i < len(a), a_old[i] > 0 premise
5. ...
}
===================================================
We accept the assertion (premise) on line 2 as a fact, and the forwards assignment law
for arrays includes this fact ``for free'' as part of its postcondition.
Here is the law for array assignment:
{ assert: P }
a[e] = e' # where e contains _no mention_ of a
{ 1. a[e] == [a_old/a]e' premise
2. [a_old/a]P premise
3. ∀ 0 <= i < len(a), (i != e) —> a[i] == a_old[i] premise
4. len(a) == len(a_old) premise
...
n. Q # must not mention a_old
}
We gain the new premises in lines 3 and 4. Line 2 is used
with ∀e
to extract information about array elements that
were not affected by the assignment to a[e].
Now we have enough knowledge to make a useful deduction:
===================================================
a[n] = a[n] - 1
{ 1. a[n] == a_old[n] - 1 premise
2. ∀ 0 <= i < len(a), (i!=n) —> a[i] == a_old[i] premise
3. 0 <= n ∧ n < len(a) premise
4. ∀ 0 <= i < len(a), a_old[i] > 0 premise
5. a_old[n] > 0 ∀e 4,3
6. a[n] >= 0 algebra 1,5
(next, we salvage the facts about those a[i] such that i != n: )
... 8. 0 <= x < len(a) assumption
... 9. a_old[x] > 0 ∀e 4,8
... 10. (x!=n) —> a[x] == a_old[x] ∀e 2,8
... ... 11. x != n assumption
... ... 12. a[x] == a_old[x] —>e 10,11
... ... 13. a[x] > 0 algebra 9,12
... 14. (x!=n) —> a[x] > 0 —>i 11-13
15. ∀ 0 <= x < len(a): (x!=n) —> a[x] > 0 ∀i 8-14
16. a[n] >= 0 ∧ ∀ 0 <= x < len(a): (x!=n) —> a[x] > 0 ∧i 6,15 }
===================================================
This tedious proof shows the difficulty in reasoning precisely about
an array update with an unknown index value.
It is easy to be discouraged by the length of the
above proof, which says that the nth element of
a was changed.
For this reason, some researchers use a picture notation to encode
the assertions.
For example, the assertion,
∀ 0 <= i < len(a), a[i] > 0
Might be drawn like this:
0 1 ... len(a)-1
+--+--+-- --+--+
a = |>0|>0| ... |>0|
+--+--+-- --+--+
so that after the assignment, a[n] = a[n]-1, we deduce this
new pictorial assertion:
0 1 ... n ... len(a)-1
+--+--+- -+---+ -+--+
a = |>0|>0| ... |>=0| ... |>0|
+--+--+- -+---+ -+--+
which is meant to portray
a[n] >= 0 ∧ ∀ 0 <= x < len(a), (x!=n) —> a[x] > 0.
These pictures can be helpful for informal reasoning,
but they quickly get confusing. (For example,
where do you draw n's cell in the above picture? What if n == 0? Etc.)
Use such drawings with caution.
To summarize, the forwards assignment law for individual
array elements reads as follows:
{ assert: P }
a[e] = e' # where e contains _no mention_ of a
{ assert: a[e] == [a_old/a]e'
∧ ∀ 0 <= i < len(a), (i != e) —> a[i] == a_old[i]
∧ len(a) == len(a_old)
∧ [a_old/a]P
}
6.4 Case studies
6.4.1 In-place selection sort
When an array holds elements that can be ordered by <,
it is useful to rearrange the elements so that they are ordered (sorted).
There are several useful tecniques to sort an array's elements in place,
that is, move them around within the array until the array is sorted.
One useful and straightforward technique is selection sort,
where the unsorted segment of the array is repeatedly scanned for
the smallest element therein, which is extracted at moved to the
end of the array's sorted segment.
A trace of a selection sort would look like this:
===================================================
(sorted segment) | (unsorted segment)
v
a == ["f", "d", "c", "b", "e"]
v
a == ["b", "d", "c", "f", "e"] ("b" selected and moved to front
v by exchanging it with "f")
a == ["b", "c", "d", "f", "e",] ("c" selected and moved to front
v by exchanging it with "d")
a == ["b", "c", "d", "f", "e"] ("d" selected and moved to front
by exchanging it with itself)
(etc.) |
v
a == ["b", "c", "d", "e", "f"] (finished)
===================================================
We require a function that searches the unsorted segment of the
array and locates the position of the least element therein:
===================================================
a = ["e", "d", "a", "c", "b" , "a"] # data structure managed by this module
def select(start) :
"""select returns the index of the smallest element in array a's
segment from a[start]...a[len(a)-1]."""
{ pre: 0 <= start < len(a) }
{ post: start <= answer < len(a) ∧
∀ start <= i < len(a), a[answer] <= a[i] }
answer = start
index = start + 1
{ invariant: ∀ start <= i < index, a[answer] <= a[i] }
while index != len(a) :
if a[index] < a[answer] :
answer = index
index = index + 1
return answer
===================================================
The pre-postconditions tell us
the knowledge the function computes.
Next, define these notions of ``ordered'' and ``permuted'' for arrays:
ordered(a) = ∀ 0 < i < len(a), a[i-1] <= a[i]
perm(a, b) = (len(a) = len(b)) ∧ (elements of a == elements of b)
The second predicate states what it means for one array, a, to
have the same elements as another, b, but maybe in a different order.
It is a little informal but good enough for us to use here.
The function that does a selection sort uses a loop to
repeatedly call
select to find the elements to move to the front of the array.
Here's the function and the sketch of the proof. The loop invariant is key ---
the elements that have been already selected are moved
to the front of a are all guaranteed to be less-than-or-equal-to the elements
in a's rear that have not yet been selected:
===================================================
def selectionSort() :
"""does an in-place sort on global array a, using select."""
{ pre true
post ordered(a) ∧ perm(a_in, a) (Recall: a_in is the starting value for a) }
global a
index = 0
{ invariant ordered(a[:index]) ∧ perm(a, a_in) ∧
∀ 0 <= i < index, ∀ index <= j < len(a), a[i] <= a[j] }
while index != len(a) :
x = select(index)
{ assert: start <= x < len(a) ∧
∀ index <= i < len(a), a[x] <= a[i]
∧ invariant }
least = a[x] # exchange the least element with the one at the
a[x] = a[index] # front of the unsorted segment
a[index] = least
{ assert: ordered(a[:index]) ∧ perm(a, a_in) ∧
index <= x < len(a) ∧
a[index] = least ∧
∀ index < i < len(a), least <= a[i]
implies: ∀ 0 <= i < index, a[i] <= least
implies: ordered(a[:index+1]) ∧
∀ 0 <= i < index+1, ∀ index+1 <= j < len(a): a[i] <= a[j] }
index = index + 1
{ assert: invariant }
===================================================
The
key accomplishment of
least = a[x]
a[x] = a[index]
a[index] = least
is to move the least element in the unsorted suffix of a to
the front of that suffix. But that makes the least value eligible
to be the rear element of the sorted prefix of a.
In this way, the loop's invariant is restored as we finish with
index = index + 1.
6.4.2 Binary search
Once an array is sorted, it can be searched for a value quickly,
much like you search for a word in a dictionary: you open the
dictionary in the middle and see if you got lucky and found the
word. If so, you are finished. If the word is earlier in the dictionary,
then you ignore the back half of the book and instead split open
the front half. (And vice versa for a word located in the
back half in the dictionary.)
You repeat this technique till you find the page where your word is.
We can search a sorted array, a, for a value, v, but jumping in the
middle of a. If we find v there, we are done. Otherwise,
we repeat the step, jumping into the first half or the
second half, as needed. Eventually, we find the value (if it is there).
Here is the function, which is famous for its difficulty to
write correctly. Glance at it, then read the paragraph
underneath it, then return to the function and study its assertions:
===================================================
def search(v, lower, upper) :
"""searches for value v within array a in the range a[lower]...a[upper].
If found, returns the index where v is; if not found, returns -1"""
{ search_pre ordered(a) ∧
∀ 0 <= i < lower, a[i] < v ∧
∀ upper < j < len(a): v < a[j]
(That is, v isn't in a[:lower] and a[upper+1:].) }
{ search_post ((0 <= answer < len(a)) ∧ a[answer] == v) ∨
(answer = -1 ∧ ∀ 0 <= i < len(a), v != a[i]) }
if upper < 0 or lower > len(a)-1 or lower > upper : # empty range to search?
{ assert: (upper < 0 ∨ lower > len(a)-1 ∨ lower > upper) ∧
search_pre
implies: ∀ 0 <= i < len(a), v != a[i] }
answer = -1
{ assert: answer = -1 ∧ (∀ 0 <= i < len(a), v != a[i]),
that is, search_post }
else :
index = (lower + upper) / 2
if v == a[index] : # found v at a[index] ?
answer = index
{ assert: a[answer] == v
implies: search_post }
elif v > a[index] :
{ assert: v > a[index] ∧ search_pre
implies: ∀ 0 <= i <= index, a[i] < v
implies: [index+1/lower]search_pre }
answer = searchFor(v, index+1, upper)
{ assert: search_post }
else : # a[index] < v
{ assert: a[index] < v ∧ search_pre
implies: ∀ index <= j < len(a), v < a[j]
implies: [index-1/upper]search_pre }
answer = searchFor(v, lower, index-1)
{ assert: search_post }
{ assert: search_post }
return answer
===================================================
To search array, a, for v, we start the function like this:
search(v, 0, len(a)-1)
The precondition is the key: to use correctly
search(v, lower, upper), we must already know that v is
not in a[0]...a[lower-1] and not in
a[upper+1}...a[len(a)-1] --- we have already narrowed the search
to the range of a[lower]...a[upper].
The function builds on this fact to narrow further the search in subsequent
self-calls until v is found or there is an empty range left to search.
The previous two examples display a style of documentation
that is used when correctness is critical and one is unable
to perform enough testing to generate high confidence that the
coding is correctly --- the program must be correct from the first
time is it used. Such an approach is taken with safety-critical
systems, where money and life depend on the correct functioning
of software from the moment it is installed.
6.4.3 Maintaining a board game: programming by contract
Many programs maintain a data structure like an edit buffer or
a spreadsheet or a game board. Typically, the data structure
is grouped with its maintenance functions (in its own module or class).
This is often called the model component, because the
data structure is a computerized ``model'' of a real-life object.
Next, there is a controller component
(module/class) that interacts with
the user and calls the maintenance functions in the model component.
(The controller sets the protocol and ``controls'' and ``connects''
the interactions
between user and model.)
If there is a graphical user interface to paint and maintain,
yet another component, called the view, must be written.
This trio of components forms a standard software architecture,
called the model-view-controller architecture.
To build such a system, we must document the internal
structure and connection points of each component so that the system
can be connected correctly. This documentation is exactly the
pre- and post-conditions for the functions in each component
as well as the
invariants for the data structures therein.
Here is a small example. It is an implementation of a tic-tac-toe
game that follows the usual rules.
First, there is the model module, which models the game board as
an array.
The game board has an important invariant
that ensures that only legal game tokens are placed on the board.
There is another data structure in this module that remembers the history of
moves made on the board.
Both data structures are documented with their invariants.
(If you are programming in an object-oriented language and have
written a class to model the game board, you call the data-structure
invariants, class invariants.
===================================================
"""module GameBoard models a Tic-Tac-Toe board.
There are two key data structures:
--- board, the game board, which holds the players' moves
--- history, a list of all the moves made during the game
The data structures are managed by calling the functions defined
in this module.
"""
# The game players:
X = "X"
O = "O"
NOBODY = "neither player"
###### The game board, a matrix sized dimension x dimension:
EMPTY = "_" # marks an empty square on the board
dimension = 3
BOARDSIZE = dimension * dimension
# the board itself:
board = [] # construct the board with this loop:
i = 0
while i != dimension :
board.append(dimension * [EMPTY])
i = i + 1
"""{ global invariant for board: Only legal markers are placed on it
ALL 0 < i,j < dimension,
board[i][j] == X v board[i][j] == O v board[i][j] == EMPTY }"""
#### A history log of all the moves: it is a list of Marker, Row, Col tuples:
history = []
"""{ global invariant for history: All moves in history recorded in board
forall 0 < i < len(history), history[i]==(m,r,c) and board[r,c] == m
}"""
### Functions that manage the board and history:
def printBoard() :
"""prints the board on the display"""
"""{ pre true
post forall 0 <= i,j < dimension, board[i][j] is printed }"""
counter = 0
for row in board :
for square in row :
if square != EMPTY :
print square,
else :
print counter,
counter = counter + 1
print
print
#print history
def emptyAt(position) :
"""examines the ith square on board; returns whether it equals EMPTY.
params: position - an int that falls between 0 and the BOARDSIZE
returns: whether or not square number position on board is EMPTY
"""
"""{ pre 0 <= position < BOARDSIZE
post answer == (board[position/dimension][position%dimension] == EMPTY) }"""
answer = False
(row,col) = (position/dimension, position%dimension)
if 0 <= row and row < dimension and 0 <= col and col < dimension \
and board[row][col] == EMPTY :
answer = True
return answer
def move(marker, position) :
"""attempts to move marker into the board at position
params: marker - a string, should be X or O
position -- an int, should be between 0 and the BOARDSIZE
"""
"""{ pre ((marker == X) v (marker == O)) & (0 <= position < BOARDSIZE)
post invariants for board and history are maintained }"""
global history, board # because we update these global variabes,
# we are OBLIGATED to maintain their invariants!
if emptyAt(position) :
(row,col) = (position/dimension, position%dimension)
board[row][col] = marker
history = history + [(marker,row,col)]
else :
pass
def winnerIs(mark) :
"""checks the game board to see if mark is the winner.
parameter: mark - a string, should be X or O
returns: mark, if it fills a complete row, column, or diagonal of
the board; returns NOBODY, otherwise.
"""
"""{ pre (mark == X) v (mark == O)
post: (answer == mark --> mark has filled a row or column or diagonal)
and (answer == NOBODY) --> mark has not filled any row/col/diag}"""
def winnerAlong(vector) :
"""sees if all the elements in vector are filled by mark"""
check = True
for index in range(dimension):
check = check and (vector[index] == mark)
return check
# check row i and column i for i in 0,1,...,dimension-1:
for i in range(dimension) :
columni = []
for j in range(dimension):
columni = columni + [board[j][i]]
if winnerAlong(board[i]) or winnerAlong(columni) :
return mark
# check the left and right diagonals:
ldiag = []
rdiag = []
for i in range(dimension):
ldiag = ldiag + [board[i][i]]
rdiag = rdiag + [board[i][(dimension-1)-i]]
if winnerAlong(ldiag) or winnerAlong(rdiag) :
return mark
# else, no winner, so
return NOBODY
===================================================
The data-structure invariants establish the internal well-formedness of
the game board, and the maintenance functions are obligated
to preserve and maintain
the invariants.
In addition, each function is documented with its own pre-post conditions
that specify how the function should be called and what the function
guarantees if it is called correctly. In the above coding, both
informal English and formal logical specifications are written.
Whether one writes English or logic depends on how critical
absolute correctness might be. (Frankly, some programs, e.g.,
toys and games, need not be absolutely correct.)
The other module of this little example is the
main program --- the controller module --- which enforces the rules of the
game, that is, the proper interaction of
the game's players with the
game board. The controller's main loop has its own invariant that asserts this point.
The loop
- displays the game board
- requests a player's next move
- implements the move on the board
Study the loop invariant first before you study anything else.
===================================================
"""The Main module controls the tic-tac-toe game."""
import GameBoard
from GameBoard import *
def readInt(message):
"""readInt is a helper function that reads an int from the display.
If we had a View Module that painted a GUI, this function would
be found there.
param: message a string
returns: an int, denoting the number typed by a player
"""
"""{ pre: message:String
post: answer:int }"""
needInput = True
answer = ""
while needInput :
text = raw_input(message)
if text.isdigit() :
answer = int(text)
needInput = False
return answer
player = X # whose turn is it? who goes first?
count = 0 # how many moves have been made?
winner = NOBODY # who is the winner?
"""{ loop invariant: The rules of the tic-tac-toe game are enforced:
(i) players take turns moving:
forall 0 <= i < count,
(i % 2)== 0 --> history[i][0] == X and
(i % 2)== 1 --> history[i][0] = O
(ii) all moves are recorded on board:
invariant for history remains true;
(iii) board holds only legal game markers:
invariant for board remains true
(NOTE: (ii) and (iii) should hold _automatically provided
that we use the board's maintenance functions.)
}"""
while winner == NOBODY and count != BOARDSIZE :
printBoard()
# get the next move:
awaitingMove = True
while awaitingMove :
"""{ invariant
awaitingMove --> (0 <= m < BOARDSIZE) and emptyAt(m) }"""
m = readInt("Player " + player + \
": type next move (0.." + str(BOARDSIZE) + "): ")
if (0 <= m) and (m < BOARDSIZE) and emptyAt(m) :
awaitingMove = False
# we have received a legal move:
"""{ assert: ((player == X) v (player == O))
and (0 <= m < BOARDSIZE) and emptyAt(m)
implies: [player/marker][m/position]move_pre }"""
move(player, m)
"""{ assert: movepost, that is,
invariants for board and history are maintained }"""
# determine whether this player is the winner:
winner = winnerIs(player)
# switch players for the next round:
if player == X :
player = O
else :
player = X
count = count + 1
"""{ assert: loop invariant, all 3 parts, holds }"""
# the loop quit, and the game's over:
print winner + " won!"
printBoard()
===================================================
Note how the controller uses the pre-post-conditions for the board's
maintenance functions to fulfill its own invariants.
In this way, we depend on the documentation from one module to
program correctly another. Programming in this style is sometimes
called programming by contract.
6.5 Equivalences in predicate logic
Here are some important equivalences in predicate logic. (We include
the Pbc-rule to prove the third and fourth ones.)
-
∀x ∀y P_xy −||− ∀y ∀x P_xy
-
∃x ∃y P_xy −||− ∃y ∃x P_xy
-
¬(∀x P_x) −||− ∃x ¬P_x
-
¬(∃x P_x) −||− ∀x ¬P_x
-
Q ∧ (∀x P_x) −||− ∀x (Q ∧ P_x) (where x does not appear in Q)
-
Q ∨ (∀x P_x) −||− ∀x (Q ∨ P_x) (where x does not appear in Q)
-
Q ∧ (∃x P_x) −||− ∃x (Q ∧ P_x) (where x does not appear in Q)
-
Q ∨ (∃x P_x) −||− ∃x (Q ∨ P_x) (where x does not appear in Q)
6.6 Predicate logic without the existential quantifier: Skolem functions
Complexity arises in predicate logic when a proposition
contains a mix of ∀ and ∃. Recall that
∀x ∃y P(x,y) asserts that each element named by x
``has its own personal'' y to make P(x,y) true. (``Everyone
has a boss.'')
In contrast, ∃y ∀x P(x,y) identifies one single individual
that is related to all elements, x, to make P(x,y) true.
(``There is one boss who is the boss of everyone.'')
Logicians have developed a form of predicate logic that omits the
existential quantifier and uses instead terms called Skolem
functions to name the values represented by each ∃y.
A Skolem function is a function name
that is used to designate where an existential quantifier should appear.
Examples explain the idea best:
===================================================
Everyone has a boss: ∀x ∃y P(x,y)
(expressed with a Skolem function,
named boss:) ∀x P(x, boss(x))
There is a single boss of everyone: ∃y ∀x P(x,y)
(expressed with a Skolem function,
named bigb:) ∀x P(x, bigb())
For every husband and wife, there
is a minister who married them: ∀x ∀y ∃z M(z,x,y)
(expressed with a Skolem function,
named minister:) ∀x ∀y M(minister(x,y),x,y)
Every two ints can be added into
a sum: ∀x ∀y ∃z F(x,y,z)
(expressed with a Skolem function,
named sum:) ∀x ∀y F(x,y,sum(x,y))
Every boss has a secretary,
who talks with everyone: ∀x ∃y (isSec(y) ∧ ∀z talks(x,z))
(expressed with a Skolem function,
named s:) ∀x (isSec(s(x)) ∧ ∀z talks(s(x),z))
===================================================
The examples show how the Skolem function acts as a ``witness'' to the
missing ∃ without revealing the identity of the individual discussed.
You can also see the difference in the first two examples between
boss(x) and bigb() --- the first example makes clear how the boss is
a function of which x in the domain is considered; the second one
makes clear that the boss is independent of all the individuals in the domain.
It is possible to work proofs in predicate logic with
Skolem functions. Here are two examples:
===================================================
∀x isMortal(x) —> hasSoul(x), isMortal(socrates()) |− hasSoul(t())
1. ∀x isMortal(x) —> hasSoul(x) premise
2. isMortal(socrates()) premise
3. isMortal(socrates()) —> hasSoul(socrates()) ∀e 1
4. hasSoul(socrates()) —>e 3,2
6. hasSoul(t()) def t(): return socrates()
===================================================
Here, the individual, Socrates, is represented as a constant
Skolem function, socrates().
The key step is the last one, where the desired Skolem function,
t(), is defined in terms of socrates():
def t() :
return socrates()
This function definition takes the
place of ∃i.
In the previous example, we could have read isMortal(socrates())
as a shorthand for ∃socrates (isMortal(socrates)).
Now, there is no practical difference.
Here is the boss-worker example (``if someone is the boss of everyone,
then everyone has a boss''):
===================================================
∀x isBossOf(x, big()) |− ∀x isBossOf(x, b(x))
1. ∀x isBossOf(x, big()) premise
... 2. a
... 3. isBossOf(a, big()) ∀e 1
... 4. hasBoss(a, b(a)) def b(a): return big()
5. ∀x is BossOf(x, b(x)) ∀i 2-4
===================================================
Notice how the defined Skolem function, b(a), disregards its
argument and always returns big() as its answer. This is because
big() is truly a's boss, no matter what argument is assigned
to parameter a.
Like before, it is impossible to prove
∀x isBossOf(x, b(x)) |− ∀x isBossOf(x, big()) ---
there is no way to define a Skolem function, def big() : ... b(x) ..., because a value for
parameter x is required. In this way, the Skolem functions
``remember'' the placement and use of the original existential
quantifiers.
The technical reasoning why Skolem functions work correctly
requires so-called Herbrand models and
the Henkin completeness theorem. But the programming intuition
given here --- defining Skolem functions as Python functions --- works
surprisingly well.
6.7 Resolution theorem proving for predicate logic
Skolem functions make it possible to adapt the
resolution-theorem-proving technique from the previous
chapter to predicate logic. The key idea is to convert all
propositions into and-or form, remove
the existential quantifers, then move and remove the universal
quantifiers (!), then complete the transformation into conjunctive-normal
form.
Then, we can perform resolution theorem proving
with the aid of unification (two-way matching) of Skolem functions.
Conversion into clause form
Conjunctive-normal form for predicate calculus is called clause form.
We achieve clause form in these steps:
-
First, rename as needed all variables, x, used within all
quantifiers, ∀x and
∃x, so that each occurrence of a quantifier appears with a unique
variable name.
-
Remove all implications, A —> B, with this
equivalence:
A —> B −||− ¬A ∨ B
-
Next, move all remaining negation operators inwards, by repeatedly
applying these equivalences:
¬(A ∧ B) −||− ¬A ∨ ¬B
¬(A ∨ B) −||− ¬A ∧ ¬B
¬(∀x A) −||− ∃x ¬A
¬(∃x A) −||− ∀x ¬A
and wherever it appears, replace ¬¬A by A.
-
Remove all existential quantifiers, replacing their variables
by Skolem functions.
-
Use these equivalences to move all occurrences of
universal quantifiers to the leftmost position of the proposition:
Q ∧ (∀x P_x) −||− ∀x (Q ∧ P_x)
Q ∨ (∀x P_x) −||− ∀x (Q ∨ P_x)
(This is called prenex form.)
Now, remove the quantifiers because they are no longer
needed (!).
-
At this point, all quantifiers are removed, and the proposition
is a combination of conjunctions, disjunctions, and negations attached
to primitive propositions that hold Skolem functions.
To finish, apply this equivalence to
move all disjunction operators inward:
(A ∧ B) ∨ C −||− (A ∨ C) ∧ (B ∨ C)
Here is an example conversion:
(∃y ∀x isBossOf(y,x)) —> (∃x isBossOf(x,x))
===================================================
1. (∃y ∀x isBossOf(y,x)) —> (∃z isBossOf(z,z))
2. ¬(∃y ∀x isBossOf(y,x)) ∨ (∃z isBossOf(z,z))
3. (∀y ¬∀x isBossOf(y,x)) ∨ (∃z isBossOf(z,z))
(∀y ∃x ¬isBossOf(y,x)) ∨ (∃z isBossOf(z,z))
4. (∀y ¬isBossOf(y, x(y)) ∨ isBossOf(z(),z())
5. ∀y ( ¬isBossOf(y, x(y)) ∨ isBossOf(z(),z()) )
(¬isBossOf(y, x(y))) ∨ isBossOf(z(),z())
6. (no need to rearrange any ∧s and ∨s)
===================================================
At this point, we can apply the resolution algorithm.
The resolution rule is slightly modified to handle the variables
and Skolem functions: a form of two-way matching, called unification,
is used to apply the ∀e rule to variables and
Skolem functions:
A ∨ P(E1) ¬P(E2) ∨ B matches = unify(E1,E2)
res: ---------------------------------------------------------
[matches](A ∨ B)
Since P is now a predicate (like isBossOf or isMortal or >),
we must unify the arguments E1 and E2 in P(E1) and P(E2) so
that they become one and the same.
It works like this:
For example,
===================================================
for isMortal(soc()) ¬isMortal(z), unify(soc(),z) = [z=soc()]
for isMortal(x) ¬isMortal(y), unify(x,y) = [x=y]
for isBoss(a(),x) ¬isBoss(y,b()), unify((a(),x), (y,b())) = [y=a(), x=b()]
for isBoss(a(),x) ¬isBoss(b(),b()), unify((a(),x), (b(),b())) = FAILURE
===================================================
The matches that are computed are applied to the remaining clauses.
For example,
¬P(x) ∨ Q(x) P(a())
-------------------------------
Q(a())
because matches(x,a()) = [x=a()], so [x=a()]Q(x) is Q(a()).
We apply the revised resolution rule to proving contradictions,
like we did with propositional logic. The resolution rule plus
unification searches for a witness to a contradiction.
Here are two examples of resolution proofs conducted with unification:
===================================================
∀x (P(x) —> Q(x)), ∃y P(y) |− ∃z Q(z)
The clauses resulting from the two premises and negated goal are
¬P(x) ∨ Q(x), P(y()), ¬Q(z)
The resolution proof goes
¬P(x) ∨ Q(x) P(y()) ¬Q(z)
| | |
+--------------+ |
| [x=y()] |
Q(y()) |
| |
+------------------+
| [z=y()]
[]
===================================================
Here is another example, the workers-and-bosses proof:
===================================================
∃y ∀x isBossOf(y,x) |− ∀u ∃v isBossOf(v,u)
isBossOf(y(),x) ¬isBossOf(v, u())
| |
+------------------------+
| [v=y(), x=u()]
[]
===================================================
Because a clause can be used more than once in a proof,
and because a variable can be set to a new value each time
it is unified in a resolution step, there is no guarantee that
the algorithm will always terminate with success or failure.
This is not a flaw of the algorithm --- predicate logic is
incomplete in that there can be no algorithm that can
decide whether or not a sequent can be proved.
Resolution is about as good as we can do in this regard.
6.8 Soundness and completeness of deduction rules
Once again, it is time to consider what propositions mean and
how it is that ∀i, ∀e, ∃i, ∃e preserve
meaning.
At this point, it would be good to review the section on models
for propositional logic in Chapter 5. There, we saw that
the connectives, ∧, ∨, ¬, —> were understood in terms
of truth tables. Also, the primitive propositions were just letters
like P, Q, and R, which were interpreted as either True or False.
Within predicate logic, we use predicates, like isMortal() and >,
to build propsitions, and we might also use functions, like
+, within the predicates. We must give meanings to all predicates
and functions so that we can decide whether propositions like
isMortal(God) and (3+1)>x are True or False.
The act of giving meanings to the predicates and functions is called
an interpretation.
Interpretations
When we write propositions in a logic, we use predicates
and function symbols (e.g., ∀i (i*2)>i).
An interpretation gives the meaning of
- the underlying domain --- what set of
elements it names;
-
each function symbol --- what answers it computes
from its arguments from the domain; and
-
each predicate --- which
combinations of arguments from the domain lead to True answers and False
answers.
Here is an example.
Say we have the function symbols, +,-,*,/, and
predicate symbols, >,=. What do these names and symbols mean?
We must interpret them
-
The standard interpretation of arithmetic is that
int
names the set of all integers; +,-,*,/ name
integer addition, subtraction, multiplication, and division, and
= and > name integer equality comparison
and integer less-than comparison.
With this interpretation of arithmetic, we can interpret propositions.
For example, ∀i (i*2)>i interprets to False,
and ∃j (j*j)=j interprets to True.
If we use any extra, ``constant names,'' (e.g., pi), we must give
meanings to the constants, also.
-
Now, given function names +,-,*,/,
and predicates, =, >, we can choose to interpret them in another
way. For example, we might interpret the underlying domain as just
the nonnegative integers. We can interpret +,*,/,>,= as the usual
operations on ints, but we must give a different meaning to -.
We might define m - n == 0, whenever n > m.
-
Yet another interpretation is to say that the domain is just {0,1};
the functions are the usual arithmetic operations on 0,1, modulo 2;
and > is defined 1 > 0 (and that's it).
These three examples show that the symbols in a logic can be interpreted
in multiple different ways. (In Chapter 5, we called an interpretation
a ``context.'' In this chapter, we see that a ``context'' is quite
complex --- domain, functions, and predicates.)
Here is a second example. There are no functions, and
the predicates are isMortal(_), isLeftHanded(_), isMarriedTo(_,_).
An interpretation might make all (living) members of the human race
as the domain; make isMortal(h) True for every human, h;
make isLeftHanded(j) True for exactly those humans, j,
who are left handed; and set isMarriedTo(m,f) True for all
pairs of humans m, f, who have their marriage document in hand.
You get the idea....
We can ask whether a proposition is True
within one specific interpretation, and we can ask whether a proposition
is True within all possible interpretations. This leads to the
notions of soundness and completeness for predicate logic:
A sequent, P_1, P_2, ..., P_n |− Q is
valid in an interpretation, I, provided that when
all of P_1, P_2, ..., P_n are True in interpretation I, so is Q.
The sequent is valid exactly when it is valid in all possible
interpretations. We have these results for the rules of propositional
logic plus ∀i, ∀e, ∃i, ∃e:
-
soundness:
When we use the deduction rules to prove that
P_1, P_2, ..., P_n |− Q,
then the sequent is valid (in all possible interpretations).
-
completeness:
When
P_1, P_2, ..., P_n |− Q is valid (in all possible interpretations),
then we can use the deduction rules to prove the sequent.
Note that, if P_1, P_2, ..., P_n |− Q is valid in just
one specific interpretation, we are not guaranteed that our rules will
prove it. This is a famous trouble spot: For centuries, mathematicians
were searching for a set of deduction rules that could be used to build
logic proofs of all the True propositions of arithmetic, that is,
the language of int, +,-,*,/,>,=. No appropriate rule set was devised.
In the early 20th century, Kurt Gödel showed that it is impossible
to formulate a sound set of rules customized for arithmetic that will prove
exactly the True facts of arithmetic.
Gödel showed
this by formulating True propositions in arithmetic notation that talked about
the computational power of the proof rules themselves, making it
impossible for the proof rules to reason completely about themselves.
The form of proposition he coded in logic+arithmetic stated
``I cannot be proved.'' If this proposition is False, it means the
proposition can be proved.
But this would make the rule set unsound, because it proved a False claim.
The only possibility is that the proposition is True (and it cannot be proved).
Hence, the proof rules remain sound but are incomplete.
Gödel's construction, called diagonalization, opened the
door to the modern theory of computer science, called computability
theory, where techniques from logic are used to analyze
computer programs. Computability theory tells us what
problems computers cannot solve, and why, and so we shouldn't try.
(For example, it is impossible to build a program-termination
checker that works on all programs --- the checker won't work on itself!)
There is also an offshoot of computability theory, called
computational complexity theory, that studies what can
be solved and how fast an algorithm can solve it.
Given an interpretation of a predicate logic, we can say that the ``meaning''
of a proposition is exactly the set of interpretations (cf. Chapter 5 --- ``contexts'') in which
the proposition is True. This returns us to the Boolean-algebra model
of logic in Chapter 5. Or, we can organize the interpretations so
that an interpretation grows in its domain and knowledge
over time. This returns us to the Kripke models of Chapter 5.
Or, we can introduce two new programming constructs, the
abstract data type and the parametric polymorphic function
and extend the Heyting interpretation
in Chapter 5.
All of these are possible and are studied in a typical second course on logic.
6.9 Summary
Here are the rules for the quantifiers, stated in terms of their
tactics:
-
(***) ∀i: use to prove Premises |− ∀x P_x:
1. Premises premise
... i. a
(fill in)
... j. P_a
k. ∀x P_x ∀i i-j
-
(***) ∃e-tactic: use to prove Premises, ∃x P_x |− Q:
1. Premises premise
2. ∃x P_x premise
... i. a P_a assumption
(fill in)
... j. Q (does not mention a!)
k. Q ∃e 2,i-j
-
(*) ∀e-tactic: use to prove Premises, ∀x P_x |− Q,
1. Premises premise
2. ∀x P_x premise
. . .
j. P_i ∀e 2 (where individual i appears earlier in the proof)
(fill in)
k. Q
-
(*) ∃i-tactic: use to prove Premises |− ∃x P_x:
1. Premises premise
(fill in)
j. P_e
k. ∃x P_x ∃i j



