Copyright © 2008 David Schmidt
Chapter 1:
Circuits that compute on numbers: Algebra
- 1.1 Algebra
- 1.2 Arithmetic circuits
- 1.3 Single-assignment programs
Circuits are ``programs'' that are constructed from
AND, OR, NOT operations and compute on the value set, {t,f}.
We use equations to name the wires within the circuit,
and we saw how to deduce properties of the circuit
even when we did not know the exact values of the circuit's inputs.
This is critical for circuit design and analysis.
We can also make
``circuits'' from the arithmetic
operations, +, -, *, /, that compute on
numbers ---
numbers travel along the wires.
We apply the principles of algebra
to deduce properties of the circuits we write.
In this chapter, we review principles of algebra and apply them
to equationally defined systems (circuits).
1.1 Algebra
An algebra is a set of (equational) laws for a set of operators.
For example, here are laws for the binary operators,
+ and *:
===================================================
(a + b) + c = a + (b + c) law assoc+
a + b = b + a law comm+
a + 0 = a law unit+
(a * b) * c = a * (b * c) law assoc*
a * b = b * a law comm*
a * 1 = a law unit*
a * (b + c) = (a * b) + (a * c) law dist
===================================================
(By the way, this set of laws defines a ring for + and *.)
Say
we use the numbers, 0, 1, 2,..., as the arguments to the operators;
then we add some equational
laws to define how the numbers are related by +1, namely,
===================================================
1 + 1 = 2
2 + 1 = 3
3 + 1 = 4
and so on, and also
0 * 0 = 0
===================================================
We use the operators and arguments to write expressions,
like (3 * 2) + 1.
We use the equational laws to calculate the expression's answer, its output,
its meaning.
The short story is that (3 * 2) + 1 = 7; the long story is that
the above equations calculate, deduce, that the expression's meaning is 7.
Here's why 3 * 2 = 6:
===================================================
3 * 2 = 3 * (1 + 1) because 1 + 1 = 2
= (3 * 1) + (3 * 1) because dist
= 3 + 3 because unit* (twice)
= 3 + (2 + 1) because 2 + 1 = 3
= 3 + (1 + 2) because comm+
= (3 + 1) + 2 because assoc+
= 4 + 2 because 3 + 1 = 4
= ... = 6 (you do the remaining steps)
===================================================
So, 3 * 2 = 6 and then (3 * 2) + 1 = 6 + 1 = 7.
A CPU does arithmetic similarly, implementing the laws by
shifting and flipping bits in its
gate layout.
1.2 Arithmetic circuits
Let's write an expression that uses variable names like x and y.
One example is (2*(x + y)) - (y + 1). Like the logic expressions
in the previous chapter, this expression uses x and y as its
"inputs."
So,
let's pretend we have hardware gates for the operations, +, -, *.
Now, we have circuits where numbers travel along the wires.
The circuit corresponding
to (2*(x + y)) - (y + 1) looks like this:
===================================================
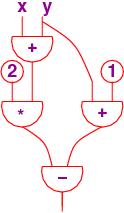 ===================================================
===================================================
In the 1970's, this form of circuit, called a data-flow program,
was used with computers with multiple processors for parallel computation
of subexpressions. They are now again being investigated for use with
multi-core processors.
Here is the equational system for the above circuit, where each internal
wire is labelled with its own name:
a = x + y
b = 2 * a
c = y + 1
d = b - c
This equation set uses one operation in each equation.
It is called three-address code and is produced by a compiler
when the compiler translates
arithmetic expressions into machine language.
Let's repeat the exercises at the end of the previous chapter for
this equational system.
First, say that x = 3 and y = 2; we can apply the algebra laws
to calculate the knowledge that holds true after each equation
is ``executed'' within the program:
===================================================
premises: x = 3, y = 2
a = x + y
therefore, x = 3, y = 2, a = x + y
therefore, x = 3, y = 2, a = 5
(by application of the previously viewed algebra laws)
b = 2 * a
therefore, x = 3, y = 2, a = 5, b = 10
c = y + 1
therefore, x = 3, y = 2, a = 5, b = 10, c = 3
d = b - c
therefore, x = 3, y = 2, a = 5, b = 10, c = 3, d = 7
===================================================
Algebra calculates the numerical values
for all of a,b,c,d. A computer does the same, but it
saves the values of the variables in storage cells.
The above
is a test case of the program.
Next, say that we know that the circuit will be plugged into an
assembly that supplies input 1 to x. What can we deduce about
the circuit's output (in terms of y)? This is a
bread-and-butter use of algebra:
===================================================
premise: x = 1
a = x + y
therefore, a = x + y, x = 1
a = 1 + y by substitution
b = 2 * a
therefore, b = 2 * a, a = 1 + y
b = 2 * (1 + y) by substitution
b = (2 * y) + 2 by algebra
c = y + 1
therefore, c = y + 1, b = (2 * y) + 2
d = b - c
therefore, d = b - c, c = y + 1, b = (2 * y) + 2
d = (2 * y) + 2 - (y + 1) by substitution
d = y + 1 by algebra
===================================================
This reasoning is similar to what we use when we write assignment
commands in a programming language.
Validating code for an embedded system
Let's do one more exercise. Say we have this equation set/circuit/program:
a = x - y
b = 2 * a
c = b + 1
Pretend that the algebra
equations define
a real-time controller for the rudder of an airplane, and inputs x and y are supplied from the plane's gyroscope, refreshed every few milliseconds. Assume that
the input value supplied by the x sensor will always be larger
than the value supplied by the y sensor, that is,
x > y must hold true. Assume also that x > 0.
Say that we want to validate, to prove,
that the value of the output, c,
is greater than one, that is, c > 1.
If so, then the code can be burned into the hardware controller and
installed in the plane.
We construct the proof with
algebra. Along the way, we will prove that a and b are positive:
===================================================
premises: x > y, x > 0
a = x - y
since x > y, then x - y > y - y then x - y > 0 by algebra
since a = x - y, then a > 0 by substitution
b = 2 * a
since a > 0, then 2 * a > 0 by algebra
then b > 0 by substitution
c = b + 1
since b > 0 then b + 1 > 0 + 1 then b + 1 > 1 by algebra
then c > 1 by substitution
===================================================
So, we have proved that when the inputs satisfy the precondition
that x > y ^ x > 0, then the equations satisfy the
postcondition that c > 1.
This style of reasoning is critical to developing correct code for
embedded, real-time systems.
Like an electronics engineer, who analyzes a circuit for
voltage and resistance levels, we have analyzed the program
and calculated in advance of execution its behavioral properties.
1.3 Single-assignment programs
The equation sets we have just studied are well behaved
because there is exactly one assignment equation for
each variable in the program. A program with this
feature is called a single-assignment program.
Further, there is
no self reference, that is, no equation, x = e, where
e references x
directly or indirectly.
If we violate either property, our analysis breaks down.
Consider this "equation set":
x = 0
y = x
x = x + 1
A naive application of algebra lets us deduce a falsehood:
===================================================
x = 0
therefore, x == 0
y = x
therefore, y == x and x == 0
x = x + 1
therefore, y == x (not any more!)
x == 0 (not any more!)
and also x == x + 1 (impossible!)
and also 0 == 0 + 1 (impossible!)
===================================================
The assignment command we use in programming
is different from an algebraic equality.
We must distinguish between
the ``old'' value of x prior to the assignment, x = x + 1,
and the ``new'' value of x that results from the assignment's ``output.''
This leads us to
programming logic in the next chapter.
Some history
By the way, the first "high level" programming language, Fortran,
was designed in the 1950s by John Backus for IBM's engineers, who wanted to write and
solve equation sets. Backus knew that computer hardware used storage cells
for variables and that the cells' values could be updated. So, he
introduced the equational version of assignment to Fortran, which wrecks the
correspondence between algebra equations and program code.
Since then, there are many modern languages, the functional programming languages,
which prohibit Fortran-style assignment and restore the connection between
algebra and program code. Backus himself, in his Turing Award Lecture of 1977,
disavowed assignment as a fundamental programming notion.
===================================================