 OR:
OR:  NOT:
NOT:  ===================================================
===================================================In this chapter, we review basic notions about gates and learn the relationship between circuits and assignment-based computer programs. This sets the stage for analyzing modern programs.
A computer does arithmetic by sensing the voltage levels at the
bits and computing new voltage levels, which are deposited
into another word. For example, the addition of two words
is done by sensing the bits of the words, right to left,
and computing new bits in the answer. Consider the addition
of 21 to 30, which we write like this:
0 0 0 1 0 1 0 1
+ 0 0 0 1 1 1 1 0
------------------
1
1
0 (with a ``carry'' of 1)
0 (because carry 1 + 0 + 1 is 0 with carry of 1)
1 (because carry 1 + 1 + 1 is 1 with carry of 1)
1 (because carry 1 + 0 + 0 is 1)
0
0
So,
0 0 1 1 0 0 1 1
(51) is deposited into a new register/word
The computation steps for each bit-addition are wired together
with electronic sensors, called gates.
There are three basic gates that suffice for doing all base-2 computations.
=================================================== AND:In the above drawings, the input wires are labelled with the names P and Q. The output that is computed is emitted from the rightmost wire that exits the gate. The AND gate emits a high voltage (1) exactly when high voltages are sensed at input wires P and Q; otherwise low voltage (0) is emitted. The gate's physical behavior is summarized by a table called a truth table:OR:
NOT:
===================================================
AND: P Q |
---------------
1 1 | 1
1 0 | 0
0 1 | 0
0 0 | 0
For the remainder of this course, we will use t (read ``true'')
for 1 and f (read ``false'') for 0. This is because we will examine
applications that go far beyond circuit theory and base 2 arithmetic.
Here are the truth tables for the AND, OR, and NOT gates:
AND: P Q | OR: P Q | NOT: P |
------------- ------------ -----------
t t | t t t | t t | f
t f | f t f | t f | t
f t | f f t | t
f f | f f f | f
Note that OR is sometimes called ``inclusive or'', because as long
as one of its inputs is true, then its output is true.
Each gate defines a one-bit arithmetic operation. (Later, we will see how to make a multi-bit operation, e.g., an 8-bit adder, as was illustrated in the example.)
It is standard to write each gate in a linear notation,
that is, instead of drawing
 ,
we write P ∧ Q instead. (The tradition of writing
linear notations to represent two-dimensional structures
goes back centuries in physics and math.)
The notations are
,
we write P ∧ Q instead. (The tradition of writing
linear notations to represent two-dimensional structures
goes back centuries in physics and math.)
The notations are
AND is ∧
OR is ∨
NOT is ¬
We can also compose the gates to define new operations.
For example, this circuit,
written ¬(P ∧ Q), defines this computation of outputs:
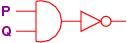
P Q | ¬(P ∧ Q)
---------------
t t | f
t f | t
f t | t
f f | t
which we can work out in stages, like this:
P Q | ¬ (P ∧ Q)
-------------------------
t t | f t t t
t f | t t f f
f t | t f f t
f f | t f f f
We write the output for each gate underneath the gate's operator
symbol. In the above example,
the circuit's final output is written in the column
underneath the NOT symbol, ¬.
We can make circuits that take three or more inputs, e.g.,
(¬(P ∧ Q)) ∨ R
computes
P Q R | (¬ (P ∧ Q) ) ∨ R
------------------------------------------
t t t | f t t t t t
t t f | f t t t f f
t f t | t t f f t t
t f f | t t f f t f
f f t | t f f t t t
f t f | t f f t t f
f t t | f f t f t t
f f f | t f f f t f
Here, the column underneath OR defines the
output. We see
this circuit emits false only when P and Q are both true and
R is false.
This is a hint that the circuit,
¬(P ∧ Q ∧ ¬R),
behaves the same way (has the same truth table) as the one above.
Yet another equivalent circuit is
(¬P) ∨ (¬Q) ∨ R. (Why?)
The examples show that
circuit theory is an arithmetic built from true, false, and
AND, OR, NOT gates.
Indeed, hardware description languages for circuit building
are little more than arithmetic expressions written to look
like assignment commands.
When we write
A = P ∧ Q
we mean that the inputs to an AND gate are wires named P and Q and
the output from the gate is a wire named A.
Using this assignment notation, we can write the earlier example,
¬(P ∧ Q),
like this:
A = P ∧ Q
OUT = ¬ A
where A and Q are the inputs to the compound circuit
and OUT is the name of the final output from the circuit.
(A is the name of an internal wire.)
We might embed the above assignment equations
into a function, like this:
===================================================
def MyGate(P, Q):
A = P ∧ Q
OUT = ¬ A
return OUT
===================================================
(We will use Python notation for our programming examples.)
Now, every time we must manufacture a MyGate for a chip,
we use the name, MyGate. Here is an example:
# say that the inputs to this circuit are X, Y, and Z, and the output is OUT:
M = MyGate(X, Y)
N = MyGate(M, Z)
OUT = ¬N
This is how computer engineers lay out modern-day circuits --- they
program them in a hardware layout language.
The point is: a circuit is a set of equations, where the variable names are the names of the wires. Later we will see how the variable names can also be the names of storage cells.
(You can skip this part if you wish.) In this section, we use hardware layout language (equations) to program an adder circuit, which is found inside every computer processor.
To do this, we must implement these two tables,
which define the two computations for one-bit addition.
The first table defines how to add the bits from two registers P and
Q (plus
the incoming carry bit, C); the
second defines how to compute the carry bit, which will
supplied to the next addition step:
ADDONE: C P Q | CARRY: C P Q |
-------------------- -------------------
t t t | t t t t | t
t t f | f t t f | t
t f t | f t f t | t
t f f | t t f f | f
f f t | t f f t | f
f t f | t f t f | f
f t t | f f t t | t
f f f | f f f f | f
For example,
ADDONE(t,t,t) = t, because a carry of 1 (true) plus the
two bits 1 and 1 (t and t) yield an answer of 1 (t).
CARRY(t,t,t) = t because the carry bit is 1 (t) also.
Here is a coding of CARRY:
def CARRY(C, P, Q) :
A = P ∧ Q
B = P ∧ R
C = Q ∧ R
OUT = (A ∨ B) ∨ C
return OUT
You are left the exercise of writing the function that
computes ADDONE from its three inputs.
(Hint: define a helper function, XOR(P,Q), that defines
(P ∨ Q) ∧ ¬(P ∧ Q), and call this function twice
in your definition of ADDONE.)
Given these two functions, we can program a 4-bit adder like this: Let register P be an array (list) of 4 t-f values; let register Q be the same. (That is, P[0] is the first (left) bit of P, P[1] is the next bit of P, etc.)
Say that we have designed (coded) ADDONE and CARRY. We can define
the adder, ADD4, which computes
as its answer an array (register) of four t-f values:
===================================================
def ADD4(P, Q, R):
"""ADD4 reads the t-f values in arrays/registers P and Q and deposits
its answer into a register, R, that holds the sum of P and Q."""
R[3] = ADDONE(False, P[3], Q[3]) # no carry when we start
C3 = CARRY(False, P[3], Q[3])
R[2] = ADDONE(C3, P[2], Q[2])
C2 = CARRY(C3, P[2], Q[2])
R[1] = ADDONE(C2, P[1], Q[1])
C1 = CARRY(C2, P[1], Q[1])
R[0] = ADDONE(C1, P[0], Q[0]) # and we lose (forget) the carry bit
===================================================
We can try it:
RegP = [0,0,1,0]
RegQ = [0,0,1,1]
RegR = [0,0,0,0]
ADD4(RegP, RegQ, RegR)
The example
adds 2 to 3 and deposits 5 into RegR (that is, [0,1,0,1]).
You can read the coding of ADD4 as a computer program, but it is also a sequence of instructions for wiring a circuit that connects to three registers (that is, three arrays of four cells each) and sends voltage levels along the connection points to alter the values in the registers' cells.
A true hardware description language would let us use loop code
to define the adder's wiring.
Here is a coding for an 8-bit adder that uses a loop:
===================================================
size = 8 # how many bits are held by a register
def ADD(P, Q, R):
"""ADD reads the t-f values in registers P and Q and deposits the
their sum into register R."""
num = size - 1
carry = False
while num >= 0 :
R[num] = ADDONE(carry, P[num], Q[num])
carry = CARRY(carry, P[num], Q[num])
num = num - 1
===================================================
A hardware fabrication machine converts code like the above into
microcode that is burned into a chip's ROM (read-only memory for its
controller) or it might
even generate a wiring layout on a chip template itself.
(In the latter case, the loop is unfolded into size-many copies, which
are translated into wirings.)
Notice that the leftmost carry bit
is lost, which is standard --- this causes arithmetic overflow.
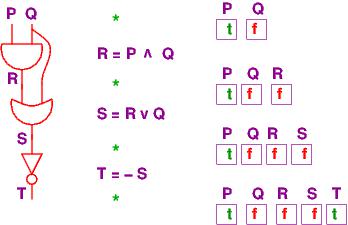
Here is a circuit:
and here is its coding in equations:
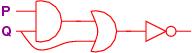
R = P ∧ Q
S = R ∨ Q
T = ¬ S
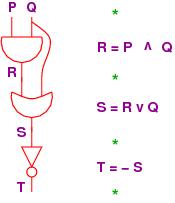
Let's redraw the circuit vertically and lay it side by side with
the assignment equations:
===================================================
Each wire in the circuit is named.
These are just variable names.
Indeed, the first (electronic) computer programs, in the 1940s, were descriptions
of wiring diagrams like this one.
 ===================================================
===================================================
The modern stored-program computer, developed by John von Neumann in the 1950s, used storage registers to hold the values of the variable names and used a processor to compute the values of the equations. In this way, a processor-plus-registers can simulate a circuit, and
Now, at each of the program points, marked by stars in the above diagram,
what information travels in the wires?
We might use the circuit with some inputs to see ``what happens.''
Say that we supply t for P and f for Q:
===================================================
The diagram shows the values on the wires labelled
P, Q, R and S
as they travel through the circuit. But this is just tracking
the values of the variables in the assignment program we wrote!
The "output variable"/write, named T, has value t.
 ===================================================
===================================================
Just as interesting is that we can analyze the program/circuit
before it is completely tested. For example, say that
the circuit will be inserted into a board where its P wire will
always receive a t as input, but we
don't know what Q will receive. What can we predict
about the circuit's behavior once it is embedded in the board? It's this:
===================================================
In the diagram, we see that R = Q is stated after the
AND gate. How do we know this?
 ===================================================
===================================================
First, we do know that R = P ∧ Q. But P = t. We substitute t for P and obtain R = t ∧ Q. Next, we do a cases analysis and consider the cases of Q's possible value: If Q is t, then t ∧ Q is t ∧ t, which simplifies to t, that is, to Q's value. Similarly, when Q is f, then t ∧ Q is f as well. Hence, in both cases, t ∧ Q equals Q.
The above reasoning is a deduction --- we deduced from the facts P = t and R = P ∧ Q that R = Q. The whole point of this course is to learn how to make such deductions.
The other deductions in the example are calculated with similar uses of substitution, simplification, and cases analysis.
The point of the previous example is that we can deduce (predict) properties of the circuit in advance of using it. These deductions complement testing.
Next, say that we don't know anything about P and Q as inputs.
What can be stated about the circuit's output? Well, it's this:
T = ¬((P ∧ Q) ∨ Q)
stating the obvious! But by a careful examination of the truth tables,
we can also state that T = ¬Q.
Later in the course, we learn deduction rules that calculate
this result, not relying on truth tables.