Trees are usually drawn pictorially like this (again, think of a ``family tree''), where data can be placed where the asterisks appear:
*
/ \
* *
/ \ /|\
* ** * *
/\ ...
...
The asterisks represent nodes; the node at
the top is the root, the tree's ``starting point.''
The arcs between nodes are called branches.
A node that has no branches underneath it is called a leaf.
Real trees grow from their root upwards to the sky, but computer-science
trees grow from the root downwards.
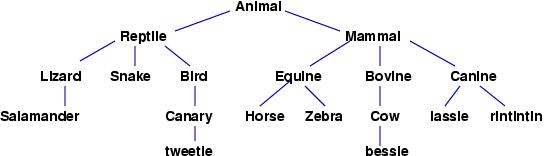
Here is an example of a tree of species, from zoology:
When we examine a non-leaf node, we see that the node has trees growing underneath it, and we say that the node has children subtrees. For example, the root node, ``Animal'', has two children subtrees.
Tree structures make an excellent alternative to arrays, especially when the data stored within them is keyed or has internal structure that allows one element to be related to, or ``saved within'' another.
Here, the leaves are used as ``end points'' and hold nothing.
We call such a tree an ordered tree or a search tree. The tree drawn above is ordered on the integer keys saved in the nodes.
The advantages of ordered trees over sorted arrays are:
QA76 book1 QA7 book2 Q17 book3 B1 book4 Z4 book5The books's keys are sequences, and the sequences label the branches of a tree that holds the books:
*
|
+-------+----------+
B | Q | Z |
* * *
1 | 1 / \ A 4 |
book4 * * book5
7 | | 7
book3 book2
| 6
book1
Books can be stored at nodes or leaves, and not all nodes hold a book
(e.g., Q1).
This tree is called a spelling tree, and it has the advantage
that the insertion and retrieval time of an object is related only
to the length of the key.
house's entrance----upper hallway----bedroom---closet---...
| | |
| | +-----private bath---...
| +---study---...
|
lower hallway---kitchen---...
|
+---lounge---...
We might imagine a robot entering the house at its entrance, knowing
nothing about what lies inside. The robot's data base looks like this:
house's entrancePerhaps the robot explores the upper hallway, bedroom, and private bath. Its data base expands with the knowledge learned during the exploration:
house's entrance----upper hallway----bedroom---closet---...
|
+-----private bath---...
As the robot explores more and more of the house, its database, a tree,
grows to include the knowledge. A tree structure is useful for
holding the knowledge, because trees can grow dynamically, spawning
branches and subtrees as needed.
A tree like the one above is sometimes called a search tree. Indeed, the search trees seen in the earlier lectures on stacks and queues also fit into this category.
int x; x = 3 + y;
STATEMENT SEQUENCE
/ \
DECLARATION ASSIGNMENT
/ \ / \
TYPE VARIABLE VARIABLE EXPRESSION
| | | / | \
int x x NUMERAL + VARIABLE
| |
3 y
The Java compiler checks the grammatical structure of a Java program
by reading the program's words and attempting to build the program's
parse tree. If successfully contructed, the parse tree is used as a guide
to help the Java compiler generate the byte code that one finds in the
program's .class file.
The tree structure is useful because it easily accommodates the creation and deletion of folders and files.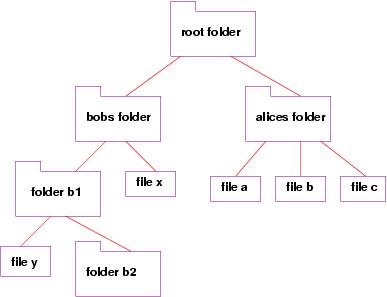
We begin study with a form of tree whose nodes have exactly two subtrees. Here is the inductive definition:
Sometimes, the arcs that enamate from the nodes are labelled so that we can describe subtrees; here, each node possess a left subtree and a right subtre..
Since trees are inductively defined, the above tree can be drawn as a layered structure:
Node----------------------------------------------------------------+ | 9 | | Node--------------+ Node------------------------------+ | | | 5 | | 12 | | | | Leaf Leaf | | Leaf Node---------------+ | | | +-----------------+ | | 15 | | | | | | Leaf Leaf | | | | | +------------------+ | | | +---------------------------------+ | +-------------------------------------------------------------------+Another representation of the above tree is
Node( 9, Node( 5, Leaf(), Leaf() )
Node( 12, Leaf(),
Node( 15, Leaf(), Leaf() )
)
)
This looks more like Java code, and it shows the nested structure of the
tree.
There is a basic pattern for computing on binary trees; the pattern follows the inductive definition. Here is what it looks like in equational form:
process( Leaf ) = ...some simple answer... process( Node(val, left, right) ) = ...compute an answer from val, process(left), and process(right)...Here is an example, which counts the number of Node-objects within a binary tree:
countNodes( Leaf ) = 0 countNodes( Node(val, left, right) ) = 1 + countNodes(left) + countNodes(right)The intuition behind the schema is simple: To count all the nodes in a big tree, we split the task into pieces:
You should apply the schema to the above example tree and calculate that it has four nodes.
package BinTree;
/** BinaryTree defines the data type of binary trees:
* (i) a leaf, or
* (ii) a node that holds a value, a left subtree, and a right subtree.
* Methods listed below should be overridden as needed by subclasses. */
public abstract class BinaryTree
{ /** value returns the value held within a tree node
* @return the value */
public Object value()
{ throw new RuntimeException("BinaryTree error: no value"); }
/** left returns the left subtree of this tree
* @return the left subtree */
public BinaryTree left()
{ throw new RuntimeException("BinaryTree error: no left subtree"); }
/** right returns the right subtree of this tree
* @return the right subtree */
public BinaryTree right()
{ throw new RuntimeException("BinaryTree error: no right subtree"); }
}
First, here is the coding for leaf objects:
package BinTree;
/** Leaf models a tree leaf---an empty tree */
public class Leaf extends BinaryTree
{ /** Constructor Leaf constructs the empty tree */
public Leaf() { }
}
Next, we write the coding for constructing node objects:
package BinTree;
/** Node models a nonempty tree node, holding a value and two subtrees */
public class Node extends BinaryTree
{ private Object val;
private BinaryTree left;
private BinaryTree right;
/** Constructor Node constructs the tree node
* @param v - the value held in the node
* @param l - the left subtree
* @param r - the right subtree */
public Node(Object v, BinaryTree l, BinaryTree r)
{ val = v;
left = l;
right = r;
}
public Object value()
{ return val; }
public BinaryTree left()
{ return left; }
public BinaryTree right()
{ return right; }
}
Notice that we have not
supplied methods to modify a tree structure
after the tree is first constructed. Surprisingly, these are not crucial ---
we can always build new trees from scratch, as we will see. (These issues
are addressed a bit later in this lecture.)
Here is the Java coding of the countNodes function, which was developed in the previous subsection:
/** countNodes returns the number of Node-objects within a tree
* @param t - the tree analyzed
* @return the number of Nodes within t */
public int countNodes(BinaryTree t)
{ int answer;
if ( t instanceof Leaf )
{ answer = 0; }
else // t must be a Node:
{ int left_answer = countNodes(t.left());
int right_answer = countNodes(t.right());
answer = 1 + left_answer + right_answer;
}
return answer;
}
You can find the classes for building binary trees here:
We might wish to print the contents of a tree's nodes:
printNodes( Leaf ) = nothing to print
printNodes( Node(value, left, right) ) = printNodes(left);
print the value;
printNodes(right);
The printing proceeds by printing the left subtree in its entirety,
followed by the value at the root, followed by the right subtree.
This is called an in-order tree traversal.
In Java,
/** printInOrder prints all the values held within a binary tree;
* the tree is traversed left-to-right _in-order_ (value printed in middle)
* @param t - the tree traversed and printed */
public void printInOrder(BinaryTree t)
{ if ( t instanceof Leaf )
{ } // no value to print
else // t must be a Node:
{ printInOrder(t.left()); // print nodes in left subtree
System.out.println( (t.value()).toString() ); // print node's value
printInOrder(t.right()); // print nodes in right subtree
}
}
For example, the tree seen earlier would print like this:
5 9 12 15
Here is a variation on the printing:
print2( Leaf ) = nothing to print
print2( Node(value, left, right) ) = print the value;
print2(left);
print2(right);
This is called a pre-order traversal and would generate
9 5 12 15for the example tree.
There is a third variation, post-order traversal, which prints a node's value after the contents of the left and right subtrees are printed. You should formulate the algorithm for post-order traversal.
BinaryTree right_subtree = new Node("c", new Leaf(), new Leaf());
It is easy to use right_subtree to build a larger tree:
BinaryTree t = new Node("a", new Leaf(), right_subtree);
Tree t holds right_subtree as its right subtree.
But the situation get more interesting if we wish to add new ``growth'' in place of one of the leaves already embedded within tree t For example, say that we wish to revise tree t so that its left subtree, a leaf, is replaced by a node that holds "b".
It is tempting to wish for a method, say, setLeft, so that we might just say:
BinaryTree new_left_subtree = new Node("b", new Leaf(), new Leaf());
t.setLeft(new_left_subtree);
Of course, we can indeed write a setLeft method (and for that matter, a setRight method) and add them to class Node:
public class Node extends BinaryTree
{ private Object val;
private BinaryTree left;
private BinaryTree right;
...
public void setLeft(BinaryTree new_left)
{ left = new_left; }
public void setRight(BinaryTree new_right)
{ right = new_right; }
}
But before we seize on this approach exclusively, we should consider
another, clever way of replacing a subpart of an existing tree.
Once again, here is tree t:
BinaryTree right_subtree = new Node("c", new Leaf(), new Leaf());
BinaryTree t = new Node("a", new Leaf(), right_subtree);
Now, we build the new_left_subtree, just like before:
BinaryTree new_left_subtree = new Node("b", new Leaf(), new Leaf());
Now we wish to alter t so that its left leaf is replaced by
new_left_subtree.
But we do not use setLeft to alter t.
Instead, we rebuild the parts of t that rest above
the new_left_subtree and reuse the other parts:
t = new Node(t.value(), new_left_subtree, t.right());This assignment statement assigns a new tree to variable t --- the tree's root value is exactly the root value that t previously held. Also, the tree's right subtree is exactly the same subtree that t previously held. But t's old left subtree, the leaf, is forgotten and new_left_subtree is used instead.
There is no need for a setLeft method --- we build a new tree instead.
The first approach, which used a setLeft method, employs mutable trees; the second method, which rebuilds the parts of the tree that rest above the altered part, uses immutable trees.
What are the comparative aspects of the two approaches? For mutable trees:
Here are the important aspects of immutable trees: