First, read the second half of Dawson, Chapter 3.
Some jobs must be solved by repeating a step over and over:
Computers became popular partly because a computer program will
unfailingly repeat a tedious task over and over.
For example, perhaps you want to know the decimal values of the
fractions (reciprocals) 1/2, 1/3, 1/4, and so on, up
to 1/20.
A painful way to calculate these is manually typing the
divisions 19 times:
print "1/2 = ", (1.0/2.0)
print "1/3 = ", (1.0/3.0)
print "1/4 = ", (1.0/4.0)
...
print "1/20 = ", (1.0/20.0)
A better solution
uses a command
called
a while loop.
At the beginning of the previous section, we saw two ``algorithms'' for tightening a car's wheel and finding a television show. We can rewrite the two algorithms in ``while-loop style,'' where we begin the algorithm with the word, ``while,'' followed by a True-False test, followed by an action to perform as long as the test is True:
A while loop is a ``repeated if-command'', for example:
if lug nut still loose :
rotate nut clockwise one turn
if lug nut still loose :
rotate nut clockwise one turn
if lug nut still loose :
rotate nut clockwise one turn
. . .
if lug nut still loose :
rotate nut clockwise one turn
. . .
We keep asking the question and doing the command until we ask
and the answer is False.
We write while-loops in Python like this:
while CONDITION :
COMMANDs
where
CONDITION is a True-False-valued expression
and COMMANDs
is a sequence of one or more commands, all indented the same amount.
The latter is called the loop's body.
With the while-loop,
we can write a program that prints
the reciprocals from 1/2 to 1/20:
==================================
# Reciprocals
# prints the reciprocals of 2 to 20.
denominator = 2
while denominator <= 20 :
print "1/" + str(denominator), "=", (1.0 / denominator)
denominator = denominator + 1
================================
Again, think of the while-loop as a ``repeated if'':
if denominator <= 20 :
print "1/" + str(denominator), "=", (1.0 / denominator)
denominator = denominator + 1
if denominator <= 20 :
print "1/" + str(denominator), "=", (1.0 / denominator)
denominator = denominator + 1
if denominator <= 20 :
print "1/" + str(denominator), "=", (1.0 / denominator)
denominator = denominator + 1
. . .
Here is the program's output:
$ python Reciprocals.py
1/2 = 0.5
1/3 = 0.333333333333
1/4 = 0.25
1/5 = 0.2
1/6 = 0.166666666667
1/7 = 0.142857142857
1/8 = 0.125
1/9 = 0.111111111111
1/10 = 0.1
1/11 = 0.0909090909091
1/12 = 0.0833333333333
1/13 = 0.0769230769231
1/14 = 0.0714285714286
1/15 = 0.0666666666667
1/16 = 0.0625
1/17 = 0.0588235294118
1/18 = 0.0555555555556
1/19 = 0.0526315789474
1/20 = 0.05
When this loop executes,
while CONDITION :
COMMANDs
the computer does the following:
Here is the flowchart representation of a
a while-loop---it is a graph with a cycle that suggests the repetition:
|
v
+------ > CONDITION ?
| / \
| True / \ False
| V |
| COMMANDS |
|_______/ |
+-------+
|
V
and indeed, this is the origin of the term, ``loop.''
denominator = 2 # Line 1
while denominator <= 20 : # 2
print "1/" + str(denominator), "=", (1.0 / denominator) # 3
denominator = denominator + 1 # 4
# 5
When the program starts, the Python interpreter has
copied the program into computer storage and has set its
instruction counter (``i.c.'')
and namespace like this:
i.c.: 1 namespace: (empty)
After instruction 1 finishes, we see the new variable, denominator,
in the name space, set
to 2:
i.c.: 2 namespace: denominator: 2
At line 2, the expression denominator <= 20 computes; it is True,
so the execution goes to Line 3:
i.c.: 3 namespace: denominator: 2
This causes 1.0 / denominator to compute to 0.5, which is printed
as
1 / 2 = 0.5.
The instruction counter moves to the next instruction:
i.c.: 4 namespace: denominator: 2
Here, denominator is increased by 1 and the instruction
counter resets to the start of the loop:
i.c.: 2 namespace: denominator: 3
For a second time, denominator <= 20 computes, and it is again
True, so the loop's body executes again:
i.c.: 3 namespace: denominator: 3
This time, instruction 3 causes 1/3 = 0.333333333333
to print.
Next, instruction 4 increments denominator, and we
repeat:
i.c.: 2 namespace: denominator: 4
The pattern repeats over and over until we reach this configuration:
i.c.: 2 namespace: denominator: 21
At this point,
the condition, denominator <= 20, computes to False,
and the instruction counter resets to the instruction that
follows the loop:
i.c.: 5 namespace: denominator: 21
You should practice execution traces with loops until they become second nature. The reasons are:
You will find it simplest to write an execution
trace in a style like that of the previos example. Let's review it:
For the reciprocals
program just seen,
denominator = 2 # Line 1
while denominator <= 20 : # 2
print "1/" + str(denominator), "=", (1.0 / denominator) # 3
denominator = denominator + 1 # 4
# 5
use a pencil and a sheet of paper and draw the
instruction counter and name space like this:
i.c. | n.s.
---------------------------------------------
1 |
As you encounter each instruction, write its line number in the left column,
and draw the variables' cells in the right column, as they appear.
When new values are inserted into the variables' cells, show the updates.
You might also write notes in your trace about the calculations
done at each command. Here is the trace after the first three
commands are completed:
i.c. | n.s.
---------------------------------------------
1 |
| denominator: 2
2 |
(True) |
3 |
(printed 1.0/2) |
Here is the trace, after Line 4, which changes the value in
denominator's cell:
i.c. | n.s.
---------------------------------------------
1 |
| denominator: X (overwritten)
2 |
(True) |
3 |
(printed 1.0/2) |
4 |
| denominator: 3
2 |
and here is the trace after a second iteration is completed:
i.c. | n.s.
---------------------------------------------
1 |
| denominator: X
2 |
(True) |
3 |
(printed 1.0/2) |
4 |
| denominator: X
2 |
(True) |
3 |
(printed 1.0/3) |
4 |
| denominator: 4
2 |
. . .
Notice how the value for denominator is updated within
the loop and notice how the handwritten trace keeps a history
of the computation from the beginning to the end. The history
can be helpful when we review the loop's progress.
countdown = 10
while countdown != 0 :
print i
countdown = countdown - 1
countdown = 5
countup = -1
while countdown > countup )
countdown = countdown - 1
print countdown, countup
countup = countup + 1
First, recall how an if-command generated its knowledge:
if CONDITION :
# assert: CONDITION
THEN_COMMANDs
# assert: GOAL
else :
# assert: not CONDITION
ELSE_COMMANDs
# assert: GOAL
# assert, in both cases: GOAL
Using the outcome of computing its CONDITION,
the if-command chose the appropriate commands for
achieving its GOAL.
Loops also have goals to achieve, and these goals must be achieved in stages. Consider yet again the reciprocals program --- its goal is to print all the reciprocals from 2 to 20. The program cannot print these with one command or one if-command; it must repeat a strategy of printing the reciprocals one at a time. While the loop is repeating, it is achieving its goal in stages. Now, we must state precisely what this means.
Recall that a loop is a ``repeated if-command.'' Here is the
knowledge production from this structure:
if CONDITION :
# assert: CONDITION
COMMANDs
# assert: PARTIAL_GOAL
if CONDITION :
# assert: CONDITION and PARTIAL_GOAL
COMMANDs
# assert: PARTIAL_GOAL
if CONDITION :
# assert: CONDITION and PARTIAL_GOAL
COMMANDs :
# assert: PARTIAL_GOAL
. . .
# assert: all in cases, not CONDITION and PARTIAL_GOAL
Note that, at each if, the CONDITION
is identical and the COMMANDs are identical.
This makes
the PARTIAL_GOAL identical at all places in the
repetition.
The goal of the reciprocals example is to print all the reciprocals from 2 to 20. The body of the program's loop prints one reciprocal. Now, say that the loop has done about half of its work --- what has it accomplished so far ?
We might say, ``the loop has printed the reciprocals from 2 to 11.'' One repetition later, what has the loop accomplished ? We might say, ``the loop has printed the reciprocals from 2 to 12.'' And so on. Notice that the partial goals are stated almost identically --- the only difference appears in the change from 11 to 12, and this difference can be described by the value of variable, denominator.
Here is the program:
denominator = 2 # Line 1
while denominator <= 20 : # 2
print "1/" + str(denominator), "=", (1.0 / denominator) # 3
denominator = denominator + 1 # 4
Here is the loop's partial goal, which is maintained at each repetition:
This is worth verifying on the loop's execution trace. We can choose
to check the partial goal either at the beginning of each repetition
or at the end --- it's the same. We'll do it at both places:
i.c. | n.s.
---------------------------------------------
1 |
| denominator: 2
2 |
(True) |
(all reciprocals from 2 to denominator - 1 have printed)
3 |
(printed 1.0/2) |
4 |
| denominator: 3
|
(all reciprocals from 2 to denominator - 1 have printed)
2 |
(True) |
(all reciprocals from 2 to denominator - 1 have printed)
3 |
(printed 1.0/3) |
4 |
| denominator: 4
|
(all reciprocals from 2 to denominator - 1 have printed)
2 |
. . .
The partial goal holds true while the loop repeats, and when the loop quits, it is because denominator holds the value, 21, implying that all the reciprocals from 2 to 20 have been printed.
This diagram illustrates the form of the argument:
|
assert: PARTIAL_GOAL accomplished
for 0 repetitions
|
v False
+-------> CONDITION ? -----------------------> assert: PARTIAL_GOAL
| | accomplised for all
| True | repetitions
| V implies: GOAL
| assert: PARTIAL_GOAL accomplished
| for i repetitions
| |
| V
| COMMANDS
| |
assert: PARTIAL_GOAL |
accomplished |
for i+1 repetitions |
|_________________+
Based on the graph, we can state
the pattern of knowledge acquisition for a while-loop:
# assert: PARTIAL_GOAL
while CONDITION :
# assert: CONDITION and PARTIAL_GOAL
COMMANDs
# assert: PARTIAL_GOAL
# assert, in all cases: not CONDITION and PARTIAL_GOAL
# implies: GOAL
The PARTIAL_GOAL is called the loop's invariant property.
The purpose of the loop's body is to maintain the PARTIAL_GOAL,
which is written in a way that states the loop's successes.
When the loop quits, the success at accomplishing and maintaining
the PARTIAL_GOAL implies that the loop's ultimate GOAL
is achieved. And every loop has an ultimate goal.
Here is the reciprocals program, annotated with its assertions:
denominator = 2
# assert: reciprocals from 2 up to denominator - 1 have printed
# (NOTE: at this point, NO reciprocals have been printed. But this is
# technically OK --- we have printed the reciprocals from 2 "up to" 1.)
while denominator <= 20 :
# assert: denominator <= 20
# and reciprocals from 2 up to denominator - 1 have printed
print "1/" + str(denominator), "=", (1.0 / denominator)
denominator = denominator + 1
# assert: reciprocals from 2 up to denominator - 1 have printed
# assert: not(denominator <= 20)
# and reciprocals from 2 up to denominator - 1 have printed
# implies: reciprocals from 2 up to 20 have printed
When the loop stops, it is because denominator > 20
(more precisely, it is 21), and this information, plus the partial
goal (invariant property) imply that the loop's goal is accomplished:
all reciprocals from 2 up to 20 were printed.
If we draw
the reciprocals program as a flowchart and use
the assertions to label the arcs, we see that the
``knowledge level'' is maintained at all positions within
the program while it is
active. As we describe in a later section in this chapter,
the knowledge levels are like voltage and amperage levels in
an electrical circuit.

We will develop the notion of loop invariant later in the chapter.
We often call a definite-iteration loop a ``counting loop,'' because there is often a variable that counts by ones while the loop repeats. (In the reciprocals example seen above, denominator does the counting.)
Here is a second example of definite iteration:
Say that we construct a program that computes the
average score of a set of student exam scores. The program first asks
the student to type the number of exams to average and then it
reads the scores, one by one,
totals them, and computes
the average. The program might behave like this:
$ python AverageScore.py
Please type the quantity of exams: 4
Type next score: 76
Type next score: 85
Type next score: 63
Type next score: 88
The average score is: 78
There is a numerical pattern to computing an average score;
if the student has taken N exams, then the average score
is calculated by this equation:
average = (score_1 + score_2 + ... + score_N) / N
The ellipsis in the formula suggests that we should
use a while-loop to
sum the scores, one by one,
until all N scores are
totalled; then we do the division. Here is a flowchart:
read N
set total = 0 # remembers the sum of all exam scores
|
V
+----> are there more
| scores to read ? --False---> average = total / N
| True |
| V
| read another score
| total = total + score
| |
+--------+
The flowchart gives the strategy we will employ --- it is a while loop.
The loop must count up to N, so we will need an extra
variable to help the loop count while it reads the N scores,
one by one.
After we read all N scores, we
calculate the average as total / N.
The flowchart algorithm is easily refined into this Python program:
FIGURE 1: while-loop to compute average score=============================
# AverageScore
# computes the average of the exam scores submitted by a user
# assumed inputs:
# N - the number of scores to read; must be a positive int
# score_, score_2, ..., score_N - a sequence of exam scores, one per line
# guaranteed output: the average of the N exam scores, computed by
# average = (score_1 + score_2 + ... + score_N) / N
N = int(raw_input("Please type the quantity of exams: "))
count = 0 # the quantity of the scores read so far
total = 0 # the points of all the scores read so far
while count != N :
score = int(raw_input("Type next score: "))
total = total + score
count = count + 1 # one more score read!
print "\nThe average is", (float(total) / N) # compute a fractional average
raw_input("\n\npress Enter to finish")
ENDFIGURE================================================================
When we test the above program, we see this behavior:
$ python AverageScore.py
Please type the quantity of exam: 4
Type next score: 78
Type next score: 86
Type next score: 67
Type next score: 92
The average is 80.75
At each iteration of the loop, another score is read and added
to the total, and the loop stops after all N scores are read
(which is when count == N).
Definite-iteration loops use a loop
counter (also called a loop index or sentry variable)
that remembers how many iterations are completed.
For a loop counter named count, the
coding pattern of definite iteration looks like this:
count = INITIAL VALUE
while THE CONDITION USING count IS TRUE :
EXECUTE COMMANDS
INCREMENT count
We saw a counting-upwards instance of the
pattern in the previous two examples:
count = START_VALUE
while count != STOP_VALUE :
COMMANDs
count = count + 1
Computer programs are structured somewhat like circuits (cf., the flowcharts we write), and newly built programs should be monitored to verify that the measurements (that is, the values of variables in the namespace) at key points in the program (e.g., at the beginning of a loop body) are acceptable. We can insert print commands to generate execution traces to do this. (If you use an IDE with a debugger, you can ask the IDE to insert breakpoints into the program.) As we saw earlier, execution traces help us understand the loops we write. Rather than write execution traces by hand, we can insert print commands into our programs that make the program generate its own execution trace that we can study carefully. We call this monitoring the program.
We need not insert a print command after every program instruction --- it suffices to insert print commands inside the bodies (indented codes) of the if and while commands and immediately after the commands finish. Each print command should state its position within the program and the values of the variables at that position.
Here is the averaging program of Figure 1, with print commands inserted
specifically for generating an execution trace:
======================================
N = int(raw_input("Please type the quantity of exams: "))
count = 0 # the quantity of the scores read so far
total = 0 # the points of all the scores read so far
while count != N :
print "(a) new iteration: N:", N, " count:", count, \
" total:", total
score = int(raw_input("Type next score: "))
total = total + score
count = count + 1 # one more score read!
print "(b) loop finished: N:", N, " count:", count, " total:", total
print "\nThe average is", (float(total) / N)
raw_input("\n\npress Enter to finish")
============================================
The print commands show how the namespace changes each time the loop
repeats. Here is the trace generated by one execution:
$ python AverageScore.py
Please type the quantity of exams: 4
(a) new iteration: N: 4 count: 0 total: 0
Type next score: 78
(a) new iteration: N: 4 count: 1 total: 78
Type next score: 86
(a) new iteration: N: 4 count: 2 total: 164
Type next score: 67
(a) new iteration: N: 4 count: 3 total: 231
Type next score: 92
(b) loop finished: N: 4 count: 4 total: 323
The average is 80.75
The trace lets us confirm that the loop correctly totals the
scores as it counts its iterations.
It you wish to ``pause'' the program while it generates its trace,
you can do this by inserting raw_input commands as well.
For example, we can pause the loop after each iteration by adding
this raw_input command after the first trace command:
while count != N :
print "(a) new iteration: N:", N, " count:", count, \
" total:", total
raw_input("Press Enter to proceed.") # pauses the execution
score = int(raw_input("Type next score: "))
total = total + score
count = count + 1 # one more score read!
When you design a program with a loop, insert print commands to generate an execution trace, and use the commands while you test your program. When you are satisfied that your program behaves properly, you can insert comment symbols at the front of the print commands to ``turn them off.''
If you have used an IDE (Integrated Development Environment) to write and test your computer programs, then you should read the IDE's user manual to learn how to use its ``breakpoint'' feature to quickly insert print-and-pause execution-trace commands like the ones we have inserted in the above example.
If a programmer wishes to monitor an assertion, she inserts an assert command into the program and tests the program some more. Recall that an assert will halt execution if the stated condition goes false.
In Chapter 2, we saw how to insert assert commands
to prevent a disastrous execution step. Here is an example:
Division
by zero is a serious computational error, and perhaps we write
some complex program code that computes a denominator for
doing reciprocals. We believe
that we have computed the denominator correctly, but at the crucial
point in the program, we demand:
... WE COMPUTE A DENOMINATOR ...
assert denominator != 0 # for the program to be structurally sound,
# denominator must have a non-zero value
reciprocal = 1.0 / denominator
...
The line marked, assert, states a critical logical property
that is required for the computation to proceed correctly.
It is a comment that states the programmer is convinced that the
prior commands computed a value for the denominator that is
non-zero. This is a crucial, structural, invariant property of the program.
It is much like a voltage level at a key place in a circuit,
calculated from the circuit's schematic by an
electronics expert.
Many times an internal specification states a key intermediate
property that leads to the program attaining its goal.
For example, if a program's goal is to obtain a ship velocity greater
than 100, but the physical device that controls the ship's accelerator
can at most double velocity at any one command, then we must
have this critical internal specification:
assert velocity > 50
velocity = velocity * 2
# goal assertion: velocity > 100
The assertion, velocity > 50, must be satisfied by the
commands that precede the one that doubles velocity for the program's
goal to be obtained.
You can imagine the importance of such internal specifications of programs for X-ray machines, airplane flight controllers, and joysticks for video games --- the programs that read signal input from these devices and direct the devices must maintain invariant properties of the devices' namespaces.
Here is a more realistic example.
Consider this little program, which was written
with good intentions:
FIGURE====================================================
# RandomReciprocal computes the reciprocal of a randomly chosen int
# in the range of 0.5 to 50.5
import random
num = (random.randrange(100) + 1) / 2
assert num > 0 # I _believe_ num is always positive ?!
print 1.0 / num
===========================================================
With an assert command,
the programmer has inserted a piece of his thinking, which
explains a crucial structural property of the program.
This program might be tested hundreds of times with no
divsion-by-zero error detected.
Nonetheless, the program holds a small flaw --- if random.randrange(100)
returns 1 as its answer, then (0+1)/2 computes to 0.
Because the programmer inserted an internal specification, another person might check the program and notice the potential error. Even if no one notices the error, then someday, sometime, the program will be used and the assert statement will detect the violation of the internal specification and announce it so that the programmer is forced to double check his work.
assert commands are a useful way to state your beliefs about the structural properties of the program you have written. They are especially useful during the programming and testing stages, and when a program is put into operation, an assert command can be used to stop a program before it does something that is truly harmful (e.g., deliver a lethal dosage of X-rays to a patient).
Think of an assert command as if it were a voltmeter probe that has been attached to a point in an electrical circuit so that the electrician can monitor the circuit over the first few days/months/years of its use.
Finally,
please note that if-commands are the preferred method for
checking the quality of external input information that cannot
be relied upon:
denominator = int(raw_input("Type an int: ")) # do we trust the human ?
if denominator == 0 :
denominator = 1 # recover by resetting the value
# assert: denominator != 0
reciprocal = 1.0 / denominator
Here, we can make no assertion about the number the human has typed,
so we use an if-command to ``filter'' bad values from the
rest of the program.
if TEST : print TRACE INFORMATION COMMANDs else : print TRACE INFORMATION COMMANDs print TRACE INFORMATIONFor loops, the ``stress points'' fall at
while TEST :
print TRACE INFORMATION
COMMANDs
print TRACE INFORMATION
assert commands are useful in the same places.
A good electronics engineer uses more than a voltmeter to analyze a circuit --- there is a schematic of the circuit and calculations of the expected voltages and amperages at the key points in the circuit. In computer programming, the ``expected'' measurements must be specified in advance by using ``external'' and ``internal'' specifications.
Just about every item you buy comes with a ``specification'' that describes how the item should be used. For example, a television comes with the specification that it should be used with 110 volts A.C. (otherwise, it will burn up).
Small electronic parts, like resistors and capacitors, come with similar specifications (e.g., a 300 volt D.C. capacitor will function properly up to 300 volts --- then, like the TV, it will burn up and explode). Steel girders also come with specifications that indicate how much weight they can hold. Such specifications are invaluable to the engineer who builds a bridge or building with the girders.
Say that you build a TV set with some resisters and capacitors. If the TV set explodes, it is because a specification of one of the internal parts has been violated (even if the TV itself was used according to its specification of voltage, temperature, and humidity). If a bridge falls down because too many big trucks crossed it simultaneously, it is because a specification of one of the bridge's parts was violated.
The specifications of resistors, capacitors, and girders establish structural invariance properties that must not be violated when the part is used.
Here is a schematic of an amplifier circuit; notice that not only
are the parts precisely specified but the levels of voltage and
resistance to the wires (pins) connected to
the amplifier's vacuum tubes are also stated:
These voltage and resistance levels can be (and should be)
measured when the amplifier is assembled and used. If there
is a variation from the actual levels from the calculated ones,
then amplifier will certainly fail (quickly).
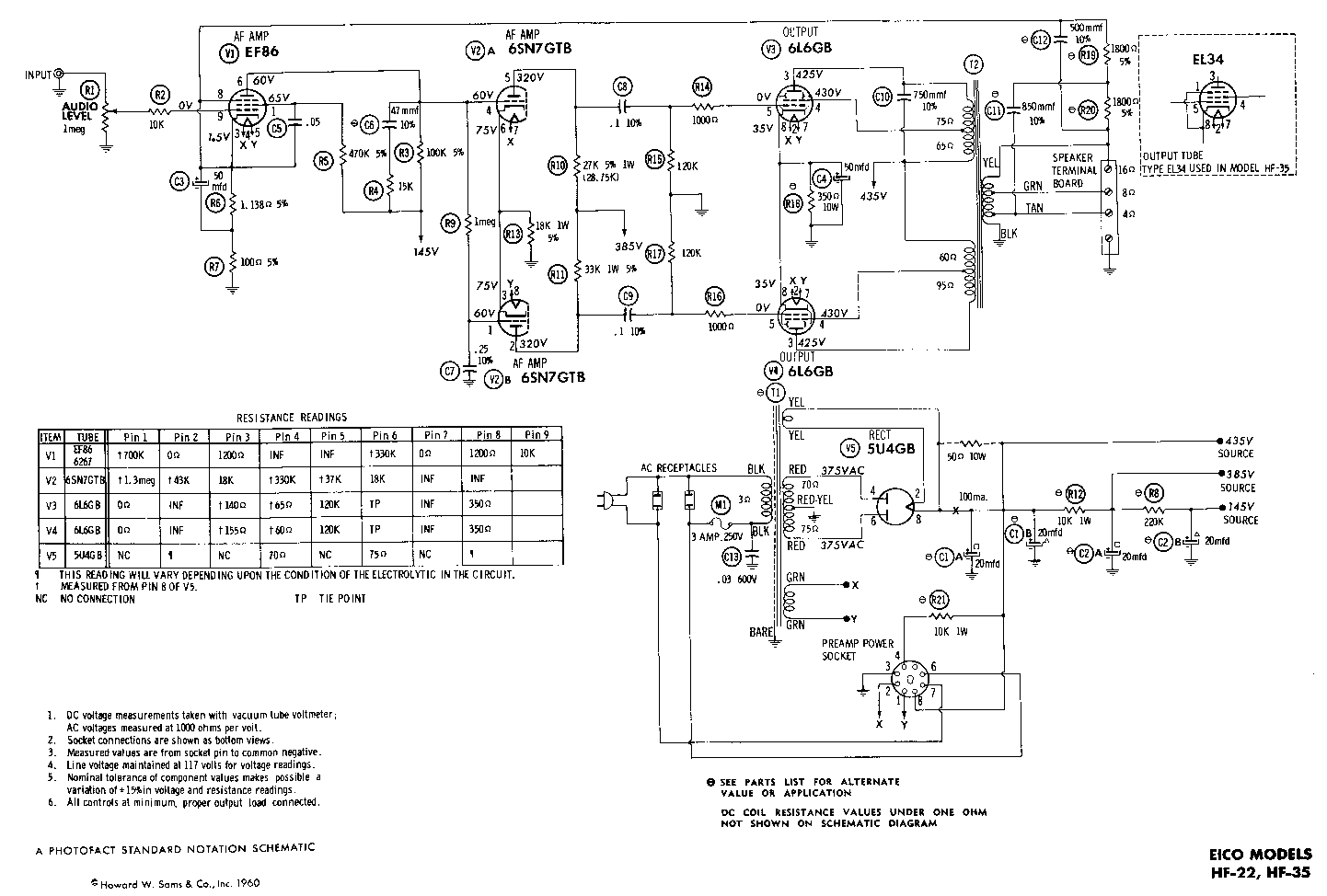
Programs are assemblies like TVs and bridges --- they are assembled from commands. All of the program examples seen in these notes began with comments that described the program's input demands and the output answers that will be computed. These comments specify what the program does. Such program specifications help others use the program correctly; the specifications document the program's behavior. Professional software designers often write the specifications before (or while) they write the program itself.
Our program specifications are written in a careful but informal English and are meant to be read like the specifications that come with the hair dryer or TV you use.
The internals of a program can be complex, and like the internals of a TV or bridge, it is important that the commands within a program are used in ways that maintain critical ``structural invariant properties'' of the program's namespace. A program's internal specifications tend to be technical, written in mathematical or logical notation, stated as True-False (boolean) logical assertions.
This is why we have practicing ``algebra'' for writing and calculating internal assertions of commands. This technique calculates the expected internal behavior of the commands in a program.
Consider the little multiplication program shown in the previous section. Perhaps we test it with 50 test cases, and each time we test it, our execution traces and assert commands and the outputs support our belief that the program computes multiplication. Although our confidence is high, all we really know from our efforts is that for 50 uses of the program, the program behaves properly. What should we do about the infinite number of test cases that we have not tried?
This is not an idle question: when an aircraft company builds a flight-controller program for an airplane, the company dare not install it in a real airplane until the program is ``known'' to be free from errors. In practice, the program is inserted into an airplane simulator and is ``flown'' and monitored (with execution traces and asserts) for some months or years of flight time. Still, there is the possibility that the flight simulator has not tested the program on some bizarre physical experience (e.g., an asteriod hits the cockpit) which might occur in practice. Should the not-completely-trusted program be inserted into real airplanes and allowed to crash and kill people someday?
When programs are used in so-called safety-critical applications (airplanes, medical equipment etc.), the programs should be diagrammed and analyzed as carefully and as completely as any electronics circuit, where the mathematical laws of electronics let a designer calculate in advance the correct levels of amperage and voltages for the points in a circuit. For computer programs, we use algebra to do similar calculations.
A loop is written to accomplish a goal in steps, and each repetition
of the loop's body should move one step closer to the goal.
When the loop's test finally computes to False, this is a signal that
the goal is achieved. A loop like this,
while CONDITION :
COMMANDs
# assert: GOAL
must be dissected and understood in terms of the partial goals it
achieves, as if it were a ``repeated if-command'':
if CONDITION :
# assert: CONDITION
COMMANDs
# assert: PARTIAL_GOAL
if CONDITION :
# assert: CONDITION and PARTIAL_GOAL
COMMANDs
# assert: PARTIAL_GOAL
if CONDITION :
# assert: CONDITION and PARTIAL_GOAL
COMMANDs :
# assert: PARTIAL_GOAL
. . .
# assert: all in cases, not CONDITION and PARTIAL_GOAL
# implies: GOAL
Note that, at each level of if (loop repetition),
the CONDITION
is identical and the COMMANDs are identical.
This makes
the PARTIAL_GOAL identical at all places in the
repetition.
We can translate this intuition into the loop structure, like this:
|
assert: PARTIAL_GOAL accomplished
for 0 repetitions
|
v False
+-------> CONDITION ? -----------------------> assert: PARTIAL_GOAL
| | accomplised for all
| True | repetitions
| V implies: GOAL
| assert: PARTIAL_GOAL accomplished
| for i repetitions
| |
| V
| COMMANDS
| |
assert: PARTIAL_GOAL |
accomplished |
for i+1 repetitions |
|_________________+
These informal ideas have a formal, logical depiction. Each repetition maintains a critical internal specification called the loop invariant --- the ``partial goal.'' When the loop finishes, we have that the successful maintenance of the partial goal by all the loop's repetitions tells us that the loop has accomplished its goal:
((loop's CONDITION == False) and (PARTIAL_GOAL holds True)) imply GOAL
In this section, we try to understand the relationship between program monitoring and loop-invariant assertions.
Here is the pattern of knowledge production of a loop, stated in
terms of the invariant:
# assert: INVARIANT
while CONDITION :
# assert: INVARIANT and PARTIAL_GOAL
COMMANDs
# assert: INVARIANT
# assert, in all cases: not CONDITION and INVARIANT
# implies: GOAL
When we print an execution trace for a program that contains a counting
(definite-iteration) loop,
we see that there is a ``pattern'' in the values of the variables
updated by the loop. This pattern gives us a big clue about
the loop's invariant. Look again at the
program that computes an average score:
======================================
N = int(raw_input("Please type the quantity of exams: "))
count = 0 # the quantity of the scores read so far
total = 0 # the points of all the scores read so far
while count != N :
print "(a) new iteration: N:", N, " count:", count, \
" total:", total
score = int(raw_input("Type next score: "))
total = total + score
count = count + 1 # one more score read!
print "(b) loop finished: N:", N, " count:", count, " total:", total
print "\nThe average is", (float(total) / N)
============================================
and its execution trace:
$ python AverageScore.py
Please type the quantity of exams: 4
(a) new iteration: N: 4 count: 0 total: 0
Type next score: 78
(a) new iteration: N: 4 count: 1 total: 78
Type next score: 86
(a) new iteration: N: 4 count: 2 total: 164
Type next score: 67
(a) new iteration: N: 4 count: 3 total: 231
Type next score: 92
(b) loop finished: N: 4 count: 4 total: 323
The average is 80.75
There is a pattern that appears at each iteration:
total holds the sum
of the scores read so far:
when count equals 1, total holds the sum of one score;
when count equals 2, total holds the sum of
two scores, and so on. No matter how often the loop repeats, the
pattern remains the same.
We can write the pattern as a mathematical equation:
for each trace line labelled by (a) and (b), this
mathematical equation holds true:
total == score_1 + score_2 + ... + score_count
(Read the underline symbol, _, as a subscript.
In this case, score_i denotes the input score that was
read at the loop's i-th iteration.
The equation is the
loop's invariant property, and
here is the averaging program with its invariant property:
FIGURE 2===================================================
N = int(raw_input("Please type the quantity of exams: "))
count = 0 # the quantity of the scores read so far
total = 0 # the points of all the scores read so far
while count != N :
# invariant: total == score_1 + score_2 + ... + score_count
score = int(raw_input("Type next score: "))
total = total + score
count = count + 1 # one more score read!
# assert: not(count != N) and total == score_1 + score_2 + ... + score_count
# implies: total == score_1 + score_2 + ... + score_N
print "\nThe average is", (float(total) / N)
=========================================================ENDFIGURE
The invariant property asserts: At the beginning of each iteration
of the loop, no matter how many times the loop body repeats, we know that
total == score_1 + score_2 + ... + score_count,
where variable count remembers how many scores were read so far.
When the loop terminates, the invariant property is still true,
and it lets us conclude that
the loop has achieved its goal:
# At the loop's conclusion, we have that count == N.
# Therefore, total == score_1 + score_2 + ... + score_N
For this reason, we know that
print "\nThe average score is", (float(total) / N)
prints the correct average score.
If we compare the above example to the pattern for loop invariants:
# assert: INVARIANT
while CONDITION :
# assert: CONDITION and INVARIANT
COMMANDs
# assert: INVARINT
# assert, in all cases: not CONDITION and INVARIANT
# implies: GOAL
we see that it matches the above example.
When the loop first starts, total is 0 and count is 0, and it is the case that total == score_1 + score_2 + ... + score_count, that is, total holds the total of all zero scores read so far. The invariant is preserved at the beginning and end of each loop repetition, and when the loop finishes, the goal is achieved.
Here is the loop from the program, drawn as a flowchart, which is a kind
of circuit schematic for the program. The assertions label the loop's
``wiring'' and show that the loop maintains an invariant
``knowledge level'':
When the loop quits, we know that total holds the sum of
all n exam scores, ensuring that the program can calculate
the correct average score by dividing by n.

All loops have invariant properties --- after all, a loop's body makes a ``pattern'' in the way it uses variables, updates them, and prints their values. When the loop repeats, its body repeats this pattern. The mathematical of loop invariants lies at the foundation of programming logics, which you will study in a later course.
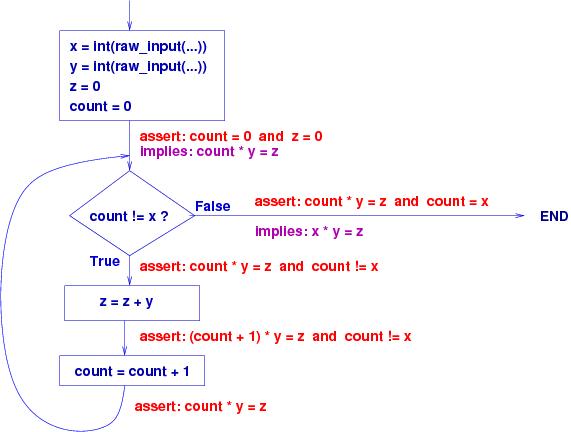
Here is a second example: What does this program print for z when
it finishes? What pattern (invariant property) is computed by its loop?
=================================================
x = int(raw_input("type an int: "))
y = int(raw_input("type another: "))
z = 0
count = 0
while count != x :
print "(a) x =", x, " y =", y, " z =", z
# invariant is ... ?
z = z + y
count = count + 1
print "(b) x =", x, " y =", y, " z =", z
print z
=====================================================
To better understand, we study the execution trace generated by the
print commands:
$ python m.py
type an int: 3
type another: 4
(a) x = 3 y = 4 count = 0 z = 0
(a) x = 3 y = 4 count = 1 z = 4
(a) x = 3 y = 4 count = 2 z = 8
(b) x = 3 y = 4 count = 3 z = 12
12
The trace information shows, when the loop starts at (a)
and after each iteration
there is this pattern (invariant):
y * count == z
Because the loop stops exactly when count == x,
we conclude that the program halts with z equalling
y * x.
The algebra for the loop in the
multiplication example is delicate. Here are all the assertions,
calculated by algebra,
inserted into the program:
================================================
x = int(raw_input("type an int: "))
y = int(raw_input("type another: "))
z = 0
# assert: z = 0
count = 0
# assert: z = 0 and count = 0
# implies: count * y = z
while count != x :
# assert: count != x and count * y = z
z = z + y
# assert: count * y = z_old and z_new = z_old + y
# implies: (count * y) + y = z_old + y
# implies: (count + 1) * y = z_new
# implies: (count + 1) * y = z (forget all facts that mention z_old)
count = count + 1
# assert: (count_old + 1) * y = z and count_new = count_old + 1
# implies: count_new * y = z
# implies: count * y = z (forget all facts that mention count_old)
# assert: not(count != x) and count * y = z
# implies: x * y = z
print z
========================================================
These assertions need not be monitored --- they are mathematical
properties (like voltage and amperage levels calculated for a circuit schematic),
and they will always hold true regardless of how the program
is tested and used.
For this reason, the program need not be tested an infinite number
of times (or even for a few months or a few days) --- the properties
are already known to be true. The program has been proved to
compute and print the product of its two inputs.
Here is the program's flowchart, labelled with the assertions:
# MaxScore # prints the highest score of the exam scores submitted by a user # assumed inputs: # howmany - the quantity of scores to read; must be nonnegative # exam_1, exam_2, ..., exam_howmany - a sequence of exam scores, one per line # guaranteed output: the largest score in the sequence of exam scores
# DropOneScore # computes the average of the exam scores submitted by a user, but # excludes the one lowest exam score # assumed inputs: # howmany - the quantity of scores to read; must be nonnegative # exam_1, exam_2, ..., exam_howmany - a sequence of exam scores, one per line # guaranteed output: the average of the howmany exam scores, forgetting # the lowest score
t = 4
count = 2
while count <= 4 :
t = t * 2
count = count + 1
I like my dog
dog my like I
summation(i) = 0 + 1 + 2 + ... + iFor example, summation(4) is 0 + 1 + 2 + 3 + 4 = 10. So, write a program that computes summation whose header line reads like this:
public int summation(int i)
product(a, b) = a * (a+1) * (a+2) * ... * b(Note: if b > a holds true, then define product(a, b) = 1.) For example, product(3, 6) is 3 * 4 * 5 * 6 = 360.
0! = 1 n! = 1 * 2 * ... * n, for positive nFor example, 5! is 1 * 1 * 2 * 3 * 4 * 5 = 120.
Look again at
AverageScore in Figure 1, which sums a sequence of
exam scores and computes their average.
What happens when the user enters a negative integer as the quantity of
exams?
$ python AverageScore.py
Please type the quantity of exams: -1
Type next exam score: 78
count = 1 ; total = 78
Type next exam score: 86
count = 2 ; total = 164
Type next exam score: 67
count = 3 ; total = 231
...
Will the program ever stop asking for exam scores? Well, no!
The loop
iterates indefinitely because its condition is always True.
Such behavior is called nontermination, or more crudely,
infinite looping or just ``looping.''
A nonterminating loop prevents execution of the commands following the loop,
in this case, preventing the program
from computing the average.
Although the program's header comment tells us to supply a nonnegative
integer as the first input, the program might defend itself
with a
conditional statement:
N = int(raw_input("Please type the quantity of exams: "))
if N <= 0 :
print "Sorry --- the quantity must be nonnegative"
else
count = 0 # the quantity of the exam scores read so far
total = 0 # the points of all the exam scores read so far
while count != N :
... # the loop proceeds as before
Some people perfer to make the loop's
entry condition check the input value:
N = int(raw_input("Please type the quantity of exams: "))
count = 0 # the quantity of the exam scores read so far
total = 0 # the points of all the exam scores read so far
while count < N :
...
If
N gets a nonnegative value, the loop refuses to iterate even once.
The second alteration is imperfect, because it lets the program
compute an erroneous result:
If N holds a negative number, then the program computes
that the exam average is 0, which is nonsensical, and if
N holds zero, the result is
even more surprising --- if you try it, you will see this:
$ python AverageScore.py
Please type the quantity of exams: 0
The average score is:
Traceback (most recent call last):
File "AverageScore.py", line 25, in ?
print "\nThe average score is:", (total / N)
ZeroDivisionError: integer division or modulo by zero
Perhaps looping is unwanted, but under no conditions do we want a program that returns a wrong answer, either. For this reason, you should take care when altering a while-loop's test to ``ensure'' termination; the alteration might cause a wrong answer to be computed and do serious damage.
If your Python program appears to have infinite looping, you can terminate it by pressing the Ctrl (control) and c keys simultaneously.
# printReciprocals # displays the decimal values of the fractions, # 1/2, 1/3, 1/4, ..., one at a time: When started, # it prints: 1/2 = 0.5 # when the user presses Return, it next prints: 1/3 = 0.3333333333 # and when the user presses Return, it prints the next reciprocal, and so on.
Many programs are designed to interact with a user indefinitely --- examples are spreadsheet programs, text editors, and interactive games. Such programs use loops. The loop does not know how many times it must iterate, so it must be prepared to do its job for as long as a user requests.
Here is an example: Say that we write a program that computes
reciprocals for whatever integers a person supplies, but quits when
the person types a 0. The program might behave like this:
$ python ReciprocalsOnDemand.py
Type an int (0 to quit): 3
1 / 3 = 0.333333333333
Type an int (0 to quit): 8
1 / 8 = 0.125
Type an int (0 to quit): 32
1 / 32 = 0.03125
Type an int (0 to quit): 60000
1 / 60000 = 1.66666666667e-05
Type an int (0 to quit): 0
Have a nice day.
The program must be designed so that it reads integers one by one,
computing their reciprocals,
until the user types a zero (and maybe this never happens!).
The algorithm for this kind of indefinite iteration looks like this:
=======================
processing = True # remembers if the computation is still going
while processing :
read num
if num == 0 :
processing = False # we are finished !
else :
print 1.0 / num
============================
Here is the complete program:
FIGURE 2: processing input transactions===========================
# ReciprocalsOnDemand
# prints the reciprocals for whatever integers the user supplies
# assumed inputs: a sequence of nonzero integers, typed one at a time,
# finished with a 0 (the signal to quit)
# guaranteed output: the reciprocals of the inputs
processing = True # remembers if the computation is still going
while processing :
# invariant: for all user inputs, correct reciprocals were printed
num = int(raw_input("Type an int (0 to quit): "))
if num == 0 :
processing = False # we are finished !
else :
print "1/" + str(num), "=", (1.0 / num)
raw_input("\nHave a nice day.")
ENDFIGURE=================================================================
An indefinite-iteration loop that does one complete task over and over again (here, printing reciprocals) has as its partial goal (invariant) the correct completion of its task for each input in the sequence of inputs supplied by the user.
The previous example showed us the
standard way to process
a sequence of input transactions that are submitted
one at a time.
Here is the pattern:
processing = True
while processing :
READ AN INPUT TRANSACTION;
if THE TRANSACTION INDICATES THAT THE LOOP SHOULD STOP :
processing = false
else :
PROCESS THE TRANSACTION
Here is a second example,
a variation of the exam-score-averaging program,
where the human does not indicate first how many scores the program
should read. Instead, the human merely types the scores, one by one,
until she types a negative score, which is the signal for the
program to quit:
FIGURE===========================================
# AverageScore
# computes the average of the exam scores submitted by a user
# assumed inputs:
# the exam scores, a sequence of nonnegative ints, terminated by
# a negative integer to read; must be a positive int
# guaranteed output: the average of the N exam scores, computed by
# average = (score_1 + score_2 + ... + score_N) / N
count = 0 # the quantity of the scores read so far
total = 0 # the points of all the scores read so far
processing = True
while processing :
# invariant: total == score_1 + score_2 + ... + score_count
score = int(raw_input("Type next score (-1 to quit): "))
if score < 0 :
processing = False
else :
total = total + score
count = count + 1
print "\nThe average is", (float(total) / count) # compute a fractional average
raw_input("\n\npress Enter to finish")
=====================================================
Here, the iterations of the indefinite-iteration loop are building towards a goal, so the loop invariant is important to the program's correctness.
while True :
READ AN INPUT TRANSACTION;
if THE TRANSACTION INDICATES THAT THE LOOP SHOULD STOP :
break
else :
PROCESS THE TRANSACTION
The break command forces an immediate exit from the loop.
Here is the reciprocal example recoded with break:
===========================================
while True :
num = int(raw_input("Type an int (0 to quit): "))
if num == 0 :
break # we are finished --- exit loop immediately
else :
print "1/" + str(num), "=", (1.0 / num)
raw_input("\nHave a nice day.")
===============================================
s = "" ... s = s + a_line_of_text + "\n"
Following is a case study that shows how we can do this in Python.
The program might behave like this, when we make an initial deposit of
$200.000, then write a check of $52.69, then ask to view the ledger,
and then quit:
$ python Checkbook.py
Type request: d(eposit), c(heck), v(iew), q(uit): d
Type amount: $200.00
Type date: April 1
Type request: d(eposit), c(heck), v(iew), q(uit): c
Type amount: $52.69
Type date and to whom payable: April 3 BookStore Co.
Type request: d(eposit), c(heck), v(iew), q(uit): v
April 1 deposit 200.00
April 3 BookStore Co. check 52.69
Current balance is: 147.31
Type request: d(eposit), c(heck), v(iew), q(uit): q
Have a nice day.
The program must keep a history,
(``ledger'') of all the transactions so that it can print them
when the user requests (by typing v).
There are two important variables that the program must maintain:
To make the program interact with its user in the behavior
shown above, we can use
the input-processing pattern seen in the previous section as the
program's ``skeleton'' (algorithm).
Because we have four forms of input command (deposit, write a check,
the main part of the input-processing pattern
is an if-elif-command. The algorithm looks like this:
balance = 0 # the account's balance starts at 0 cents
ledger = "" # the history of transactions starts empty
processing = True
while processing :
read the transaction
if transaction == "q" :
processing = False
elif transaction == "c" :
process a check-writing request (to be refined further!)
elif the transaction == "d"
process a deposit (to be refined further, also)
elif the transation == "v" :
print the contents of the ledger and the balance (ditto)
else :
the transaction is bad, so print an error message (again)
The algorithm shows there are several tasks that the program
must tell how to do.
It is too much work to write all the tasks at once and then code all of them and then test all of them; our thinking will get distracted and our testing will probably miss crucial test cases. It is better to refine and code and test each task one at a time.
Let's start with the
the deposit transition ("d"). To process a deposit,
we think about how we would write down a deposit (if we were using
pencil and paper) and would update the account balance.
We decide on these steps:
read the amount of the deposit
read the date of the deposit
add the amount of the deposit to the current balance
append the deposit info to the end of the ledger
Now we write the code in Python:
input = raw_input("Type amount: $")
dollars_and_cents = input.split(".") # This trick is explained below
dollars = int(dollars_and_cents[0]) # same here
cents = int(dollars_and_cents[1]) # same here
amount = (dollars * 100) + cents # compute the deposit in cents
date = raw_input("Type date: ")
balance = balance + amount # add the deposit to the balance
info = date + " deposit " + input
ledger = ledger + info + "\n" # add the info to the ledger
Lines 2-4 above use a trick from the previous chapter:
dollars_and_cents = input.split(".")
splits a dollars-period-cents string into its dollars and cents amounts,
which are then assigned to their respective variables:
dollars = int(dollars_and_cents[0])
cents = int(dollars_and_cents[1])
(The details of the trick are explained in Chapter 5.)
The last line shows that we add a transaction to the end of the ledger by string concatenation.
Here's the program we have written so far in Python:
===================================
# Checkbook
# maintains a ledger of checkbook transactions and a running balance
ledger = ""
balance = 0 # the account's balance starts at 0 cents
processing = True
while processing :
request = raw_input("\nType request: d(eposit), c(heck), v(iew), q(uit): ")
if request == "q" : # Quit
processing = False
elif request == "c" : # Check written
pass # process a check-writing request
elif request == "d" : # Deposit
input = raw_input("Type amount: $")
dollars_and_cents = input.split(".")
dollars = int(dollars_and_cents[0])
cents = int(dollars_and_cents[1])
amount = (dollars * 100) + cents
note = raw_input("Type date: ")
balance = balance + amount
ledger = ledger + note + " deposit " + input + "\n"
print ledger, balance # generate trace information for testing
elif request == "v" : # View all transactions
pass # print the contents of the ledger and the balance
else :
print "I don't understand your request; please try again."
raw_input("\nHave a nice day.")
========================================
We inserted the coding for doing deposits. Notice the cute trick:
the unfinished parts of the algorithm are represented by pass,
which is a Python command that stands for ``do nothing.''
Although the program is not finished, we can already test what we have! We can start the program, try it with deposit requests, and quit when we want. Once we believe that the program handles deposits correctly, we can code more of the program.
Note that we added the extra command,
print ledger, balance # generate trace information for testing
so that we can see what the program does when it executes
the deposit action.
Say that we next refine and code the command to view the ledger.
That coding is simple:
print ledger
print "Current balance is:" ,
dollars = balance / 100
cents = balance % 100
print dollars, ".", cents
We insert these instructions into the position held by
pass # print the contents of the ledger and the balance
and test the program with both ``deposit'' ("d") and ``view'' ("v") requests.
(If you test the above coding, you will find that it does not
print correctly amounts like 500.05 --- it prints
500.5 instead. This must be repaired, later.)
Once we refine and code the check request ("c"), which is similar
to the deposit part, we get this program:
FIGURE 3 ===========================================
# Checkbook
# maintains a ledger of checkbook transactions and a running balance
#
# assumed input: a series of transactions of four forms:
# (i) Deposits: type d
# then type the dollars and cents amount
# then type the date of the deposit
# (ii) Check written: type c
# then type the dollars and cents amount
# then type the date and to whom the check was addressed
# (iii) View ledger: type v
# (iv) Quit: type q
#
# guaranted output: a correct ledger, listing the sequence of deposits
# and checks, along with the final balance, generated by the v command
ledger = "" # the history of all transactions
balance = 0 # maintain the balance in cents
processing = True
while processing :
# invariant: ledger holds a history of all transactions so far
# and balance maintains the correct balance from the transactions
request = raw_input("\nType request: d(eposit), c(heck), v(iew), q(uit): ")
if request == "q" : # Quit
processing = False
elif request == "c" : # Check written
input = raw_input("Type amount: $")
dollars_and_cents = input.split(".")
dollars = int(dollars_and_cents[0])
cents = int(dollars_and_cents[1])
amount = (dollars * 100) + cents # compute the amount in cents
note = raw_input("Type date and to whom payable: ")
balance = balance - amount # deduct the check from the balance
info = note + " check " + input
ledger = ledger + info + "\n"
elif request == "d" : # Deposit
input = raw_input("Type amount: $")
dollars_and_cents = input.split(".")
dollars = int(dollars_and_cents[0])
cents = int(dollars_and_cents[1])
amount = (dollars * 100) + cents # compute the deposit in cents
date = raw_input("Type date: ")
balance = balance + amount # add the deposit to the balance
info = date + " deposit " + input
ledger = ledger + info + "\n"
elif request == "v" : # View all transactions
print ledger
print "Current balance is:" ,
dollars = balance / 100
cents = balance % 100
if cents < 10 :
print str(dollars) + ".0" + str(cents)
else :
print str(dollars) + "." + str(cents)
else :
print "I don't understand your request; please try again."
raw_input("\nHave a nice day.")
ENDFIGURE====================================================
Notice that one way of printing a correct dollars, cents amount for,
say, 500 dollars and 5 cents is by adding an if-command:
dollars = balance / 100
cents = balance % 100
if cents < 10 :
print str(dollars) + ".0" + str(cents)
else :
print str(dollars) + "." + str(cents)
There is a more clever way to insert the optional zero,
which uses a Python trick.
The trick cannot be explained just now, but it looks like this:
dollars = balance / 100
cents = balance % 100
import string # the string module has a ``magic'' operation, zfill
print str(dollars) + "." + string.zfill(cents, 2) # format cents so that
# it always prints as 2 digits
Finally, we might ask, ``What is the invariant property of the
loop in this program?'' The answer is: the loop correctly maintains
the value of balance so that it correctly added all deposits
and subtracted all checks, and
it also correctly maintains the value of
ledger so that it remembers all transactions. Perhaps
these invariants are not so simply written as mathematical equations,
but they are critical to understanding what the program does!
Loops are easily miswritten, and one big problem is that a loop's
termination condition is often carelessly written.
For example, this attempt to compute the sum, 1 + 2 + ... + n,
total = 0
i = 0
while i <= n :
i = i + 1
total = total + i
print "i = ", i, "; total = ", total # generates a trace
fails because the loop iterates one time too many.
This form of error, where a loop iterates one time too many or
one time too few, is commonly made, so be alert for it.
A related problem is an improper starting value for the variables
used by the loop,
e.g.,
total = 1
i = 1
while i <= n :
total = total + i
i = i + 1
print "i = ", i, "; total = ", total # generates a trace
This loop again attempts to compute the sum,
1 + 2 + ... + n, but it adds the value 1 twice
into its total.
Examples like these show that it is not always obvious when a loop iterates exactly the correct number of times. When you test a loop with example data, be certain to know the correct answer so that you can compare it to the loop's output.
Here is another technical problem with loop tests:
Never code a loop's
test expression as an equality of two floats (fractional numbers).
For example, this loop, which counts in thirteenths from zero to one,
d = 0.0
while d != 1.0 :
d = d + (1.0 / 13.0)
print d
should terminate in 13 iterations but loops forever
due to imprecise fractional computer arithmetic.
Testing programs with loops is more difficult than testing programs with conditionals, because it is not enough to merely test each statement in the loop body once. A loop encodes a potentially infinite number of distinct executions, implying that an infinite number of test cases might be needed. Obviously, no testing strategy can be this exhaustive.
In practice, one narrows loop testing to these test cases:
Consider yet another
attempt to compute the summation 1 + 2 + ... + n:
n = int(raw_input("Type an int: "))
total = 0
i = 0
while i != n :
total = total + i
i = i + 1
print "i = ", i, "; total = ", total # generates a trace
This program might be tested with n set to 0 (which
we believe should cause immediate
termination), set to 1 (should cause termination in one iteration),
set to, say, 4 (a typical case that requires
multiple iterations), and set to a negative number, say, -1,
(which might cause unwanted behavior).
These test cases quickly expose that the loop's condition
forces termination one iteration too soon.
Subtle errors arise when a loop's condition
stops the loop one iteration too soon or one iteration too late;
testing should try to expose these ``boundary cases.''
A more powerful version of loop testing is invariant monitoring, where you insert an assert command into the loop to monitor how the loop maintains the variables in the namespace. If the invariant is remaining true, this gives you great confidence that the loop is making proper progress towards the correct answer.
Although loop testing can never be exhaustive, please remember that any testing is preferable to none---the confidence that one has in one's program increases by the number of test cases that the program has successfully processed.
while CONDITION :
COMMANDs
The semantics goes as follows:
assert BOOLEAN_EXPRESSIONwhere BOOLEAN_EXPRESSION is an expression that computes to True or False. The semantics goes
count = INITIAL VALUE
while CONDITION ON count :
EXECUTE COMMANDs
INCREMENT count
where count is the sentry variable.
processing = True # announces when it's time to stop
while processing :
READ AN INPUT TRANSACTION
if THE INPUT INDICATES THAT THE LOOP SHOULD STOP :
processing = False
else :
PROCESS THE TRANSACTION
There is a variation on the above pattern that uses the
break command:
while True :
READ AN INPUT TRANSACTION;
if THE TRANSACTION INDICATES THAT THE LOOP SHOULD STOP :
break
else :
PROCESS THE TRANSACTION
The break causes the loop to terminate immediately,
without executing any more commands in its body.