My father used to call computer programming, ``garbage in, garbage out.'' What he meant to say is that a computer program works by accepting external, ``input'' knowledge, like numbers, which it uses to compute new, ``output'' knowledge, which it displays --- sensible input knowledge generates useful output knowledge; garbage input generates garbage output. In this lecture we learn to write programs in this classical, input-compute-output format. We learn the necessary liguistics and we encounter key design and foundational topics.
First, read Dawson, Chapter 2.
A string longer than one line is enclosed by """. Here
is an example:
print """
+--+ +--+ +--+
| | | | | |
| +---+ | | |
| +---+ | | |
| | | | | |
+--+ +--+ +--+
"""
As the example suggests, we might use a
multi-line string with a print command to
print a pattern in the command window. (Try it --- Place the above
command into a file, named TestString.py, within folder
C:\MyPython, and test the
program from a new command window:
set path=C:\Python22
cd C:\MyPython
python TestString.py
(Note: if you correctly set the Path variable, as described at the end
of the previous chapter, you won't need the first command.)
You can also write the above command like this:
print \
"""
+--+ +--+ +--+
| | | | | |
| +---+ | | |
| +---+ | | |
| | | | | |
+--+ +--+ +--+
"""
where the \ indicates that the rest of the command is
continued on the next line. The backslash can also be used to
split a long command across two lines, e.g.,
print 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 \
+ 10 + 11 + 12 + 13
which prints the sum, 91.
Finally, we can print together strings and numbers on the same
line if we separate them by commas. Here is an example:
print "The sum of", 3, "and", 2, "is", (3+2)
which prints
The sum of 3 and 2 is 5
(Notice that the arithmetic expression, (3+2), was computed
to its answer.)
We can use the commas to split the print commands across multiple lines
like this:
print "The sum of",
print 3, "and", 2,
print "is",
print 3 + 2
Place these commands in a program, say, Test.py, and try it ---
python Test.py. You will again see
The sum of 3 and 2 is 5
>>> print 2 * 3 * 4 24 >>> print 9 / 4 2 >>> print 9 % 4 1 >>> print 2 - 3 - 4 -5 >>> print 2 * (3 + 4) 14 >>> print (2 * 3) + 4 10 >>> print 2 - (3 - 4) 3In the second experiment, notice that the remainder is forgotten; in the third, it is the remainder that is retained. (9 divided by 4 has answer 2 with remainder 1.) The remaining experiments show that it is important to use parentheses to indicate the order in which the arithmetic operators should be performed.
Python lets us do arithmetic with fractions, which are called
floats (floating-point numbers).
We must type fractional numbers to indicate we are working with floats.
Here are examples:
>>> print 2.0 * 3.0
6.0
>>> print 1.0 / 3.0
0.33333333333333331
>>> print 2.0 * 3.3
6.5999999999999996
>>> print 9.0 / 4.0
2.25
>>> print 9 / 4.0
2.25
>>> print 9.00 / 4
2.25
The computer's CPU cannot do exact fractional arithmetic;
for example, we know that
1.0/3.0 is the infinite fraction of 3s,
0.333333333333333333333...3...., but the size of numbers stored in
a computer limits how precise the result can be. (This situation
can prove frustrating and even disastrous when precise
answers are required, e.g., for the Mars-rover launched from Earth that
crash landed due to an arithmetic imprecision.)
There are also surprises, like that shown
in the third example. The remaining examples show that division
on fractional numbers produce fractional answers.
It is possible to mix ints and floats in the same expression,
and the result is computed as a float. For example,
>>> print 1.0 / 3
0.33333333333333331
because the 3 is converted to 3.0 for doing the division.
minutes = hours * 60and we can use the laws of algebra to compute that 4 hours contains 240 minutes:
hours = 4 minutes = hours * 60implies that
minutes = 4 * 60 = 240
Names like minutes and hours are called
variables in algebra (the number with which we replace the
name can ``vary''), and variables are used in Python as well.
Indeed, we can write the equations verbatim in Python like this:
>>> hours = 4
>>> minutes = hours * 60
>>> print hours, "hours has", minutes, "minutes"
4 hours has 240 minutes
The equational commands are called assignments
(``the value 4 is assigned to variable hours.'')
The second command, another assignment, computes the number represented
by the expression, hours * 60. Since hours
names 4, the expression computes to 240.
The third command asks Python to display the integer computed
for variable minutes. Try it.
Here is a second example, using strings:
>>> s = "ha"
>>> t = s + s + s
>>> print t
'hahaha'
Finally, here is an equation that converts degrees celsius (centigrade)
to fahrenheit, using fractional numbers:
fahrenheit = (1.8 * celsius) + 32.0
One important feature of variables used in computer programs
is that a variable may obtain a value and later have that
value forgotten (``overwritten'') by another value.
Here is an example:
hours = 4
minutes = hours * 60
print hours, minutes
hours = 5
minutes = hours * 60
print hours, minutes
These commands (clumsily) compute the minutes within 4 hours and
5 hours by using variables hours and minutes
to do two calculations. The program will display
4 240
5 300
When hours = 5 is computed, the 4 is
forgotten (overwritten) by 5. The 4 is
lost forever.
A similar phenomenon occurs when the second assignment,
minutes = hours * 60 is computed: 240 is
overwritten by 300 and is lost forever.
You should take great care when overwriting variables with new values. This action complicates our understanding of the knowledge generated by the program. We now study precisely this issue.
Let's return to this example,
hours = 4
minutes = hours * 60
print hours, "hours has", minutes, "minutes"
and consider the knowledge that is generated and named by
each command. The first command, hours = 4,
of course generates the knowledge that there are 4 hours:
hours = 4
# assert: hours = 4
minutes = hours * 60
print hours, "hours has", minutes, "minutes"
We have inserted a comment line to summarize the knowledge that is
generated and named. We call this an assertion,
because we assert or predict the consequences of the command.
Consider the next command:
hours = 4
# assert: hours = 4
minutes = hours * 60
# assert: hours = 4 and minutes = hours * 60
print hours, "hours has", minutes, "minutes"
The second assignment command establishes an algebraic
equality, and with our knowledge of algebra, we conclude
one more important fact:
hours = 4
# assert: hours = 4
minutes = hours * 60
# assert: hours = 4 and minutes = hours * 60
# implies: minutes = 240
print hours, "hours has", minutes, "minutes"
Using a tiny bit of algebra, we calculate that
minutes = 4 * 60, which implies that
minutes = 240.
The assertions and their implications
make us confident that the program will indeed display
4 hours has 240 minutes
when it is computed.
We can draw the program as a ``straight-line circuit'' and
annotate it with the assertions:

Here is a second example: Here again is the equation for converting
a celsius temperative to fahrenheit:
fahrenheit = (1.8 * celsius) + 32.0
Say that we do not know the value of celsius, other
than it is above 0 (that is, above freezing). We can use
our knowledge of algebra like this:
# assert: celsius > 0
fahrenheit = (1.8 * celsius) + 32.0
# assert: celsius > 0 and fahrenheit = (1.8 * celsius) + 32.0
# implies: fahrenheit > 32.0
because 1.8 * celsius > 1.8 * 0, implying that
(1.8 * celsius) + 32.0 > (1.8 * 0) + 32
This example shows the form of reasoning that all skilled
software engineers apply on a daily basis. Although we do not
know the exact number that will be used for the celsius
temperature, we already understand the nature of the knowledge
generated by the computation --- temperatures
above freezing in celsius (0) generate temperatures above
freezing in fahrenheit (32):

Here is a third example, which illustrates how knowledge can
be lost during a computation:
hours = 4
minutes = hours * 60
print hours, minutes
hours = 5
minutes = hours * 60
print hours, minutes
This example was developed in the previous section, when we
noted that a variable can acquire a new value during a computation
that overwrites its previous value.
After the first two commands, we have the expected consequences:
hours = 4
# assert: hours = 4
minutes = hours * 60
# assert: hours = 4 and minutes = hours * 60
# implies: minutes = 240
print hours, minutes
hours = 5
minutes = hours * 60
print hours, minutes
What is the knowledge accumulated after we print hours
and minutes and then reset
hours = 5 ?
Clearly it is not
hours = 4 and minutes = hours * 60 and minutes = 240 and hours = 5
This is a mathematical contradiction!
Some knowledge is lost when the 4 assigned to
hours is overwritten by 5. To see precisely which facts are
lost, we restate the knowledge, annotating
the facts that were true for the old value of hours
and for the new value of hours:
hours_old = 4
minutes = hours_old * 60
minutes = 240
hours_new = 5
All facts that mention hours_old must be forgotten.
This gives us
minutes = 240
hours_new = 5
Now we drop the subscript, new, and this yields the
correct knowledge at this point in the computation:
hours = 4
# assert: hours = 4
minutes = hours * 60
# assert: hours = 4 and minutes = hours * 60
# implies: minutes = 240
print hours, minutes
hours = 5
# assert: minutes = 240 and hours = 5 <-- CORRECT !
minutes = hours * 60
print hours, minutes
Notice that there is no
algebraic relationship between the numbers named by
minutes and hours at this point.
When we finish our analysis, we determine that the
knowledge resulting from the final assignment is
minutes_old = 240
hours = 5
minutes_new = hours * 60
We forget the out-of-date fact that
minutes_old = 240, giving us
# assert: minutes = 240 and hours = 5
minutes = hours * 60
# assert: hours = 5 and minutes = hours * 60
# implies: minutes = 300
print hours, minutes
Here is the example restated as a ``straight-line'' circuit:

celsuis = 20 fahrenheit = (1.8 * celsius) + 32.0
# assert: hours > 1 and hours < 10 minutes = hours * 60
y = x x = x + 1Can you deduce that y < x at the end? Can you deduce that x = y + 1 at the end?
minutes = hours * 60and
fahrenheit = (1.8 * celsius) + 32.0define little recipes for calculation, and we saw in the previous sections how to use such equations in Python programs that calculate and print answers, e.g.,
hours = 4 minutes = hours * 60 print hours, minutesBut what if we want to calculate how many minutes are in 6 hours? 24? 48? Rather than constantly edit the program, inserting new numbers for the value of hours, we can rewrite the Python program so that it asks its human user to type the number of hours that must be converted into minutes. The information typed by the user is input to the program.
Here is a first, tiny example: Say that we write a script (program) that
repeats three times a string we type. When the program, named
Triple.py, is started,
it asks the user to type some text (a string):
$ python Triple.py
Type any string you wish:
Perhaps the user types hey! followed by the Enter key.
We see this:
$ python Triple.py
Type any string you wish: hey!
hey!hey!hey!
(Note: from now on, we use a dollar sign, $, to stand for
the prompt we see within a command window. Or, you can start a program
by double-clicking on its icon.)
When we typed hey!, we supplied input, and when the
answer appeared, it was output. Input and output are
data (information used by the program).
Here is the program, Triple.py:
====================================
# Triple repeats a string three times.
phrase = raw_input("Type any string you wish: ")
tripled = phrase + phrase + phrase
print tripled
raw_input("\n\npress Enter to finish")
=========================================
The first line is a comment, which reminds us and tells others
what the script means to do. The second line is blank, and
the third,
phrase = raw_input("Type any string you wish: ")
is a Python command that
The next command makes three copies of the string named phrase, appends them, and names the new string tripled. The command thereafter displays string tripled.
The final command is Dawson's trick that pauses the program and asks us to press the Enter key one last time before the program finishes. (This trick is useful when we start the program by double clicking on its icon in a File Window.)
Notice that we can use the script as often as we like; here's another go:
$ python Triple.py
Type any string you wish: Ha
HaHaHa
Each time, the program receives input and produces output based on the
input.
Say that we rewrite the script like this and name it TripleShout.py:
================================
# TripleShout repeats a string three times, but in upper-case letters.
phrase = raw_input("Type any string you wish: ")
phrase = phrase.upper() # .upper is a _method_
tripled = phrase + phrase + phrase
print tripled
raw_input("\n\npress Enter to finish")
=====================================
When you use this, you might see
$ python TripleShout.py
Type any string you wish: hey!
HEY!HEY!HEY!
The alteration is this new command:
phrase = phrase.upper() # .upper() is a _method_
As the comment says, the new concept is .upper(), which is
called a method. For now, think of methods as arithmetic
operations. Here, .upper() is an operation on the string
named phrase, which computes a new string that has all upper-case
letters. The upper-case string is then renamed phrase
(and the old meaning of phrase is lost forever).
We will say more about this behavior later.
Method .upper() is also a function, and you are welcome to ``read'' phrase.upper() as the function, upper(phrase). Function upper makes a new string that looks like the string named by phrase, but with upper-case letters. (We will learn later in the course the reasons why a ``method'' is written differently from a ``function'' in Python.)
Say that we write a script (program) that tells us how many minutes
are in some hours. The program is named HoursToMinutes.py,
and we would use it like this:
$ python HoursToMinutes.py
Please type an hours amount, a nonnegative int: 4
The number of minutes is 240 .
That is, we start the script, and it asks us
Please type an hours amount, a nonnegative int:
So, we type a number, say 4, and press Enter.
The answer appears:
The number of minutes is 240 .
Here, 4 is the input, and
The number of minutes is 240 . is the output.
Here is the script, HoursToMinutes.py:
FIGURE========================================
# HoursToMinutes
# This program converts hours to minutes.
# assumed input: hours - a nonnegative integer
# guaranteed output: the conversion of hours to the corresponding amount
# of minutes, a nonnegative integer
hours = int( raw_input("Please type an hours amount, a nonnegative int: "))
minutes = hours * 60
print "The number of minutes is", minutes, "."
raw_input("\n\npress Enter to finish")
ENDFIGURE===============================================
The first five lines are comments that explain the program's name and
its purpose. Lines 3-5 summarize the program's input and
output behavior and state a guarantee about the kind of output the
program will produce, assuming that the input is correctly
entered.
Such comments are crucial for packaging and selling
the program to others.
For example, if someone tries to supply a word as input, we see
$ python HoursToMinutes.py
Please type an hours amount, a nonnegative int: four
Traceback (most recent call last):
File "HoursToMinutes.py", line 7, in ?
hours = int( raw_input("Please type an hours amount, a nonnegative int: "))
ValueError: invalid literal for int(): four
The program did not behave as guaranteed because its input failed
the assumption. Instead,
we received as output a complicated explanation that the program's Line
7 did not operate properly and the program stopped there with a
ValueError (whatever that is!).
Returning to the program, we see that lines 7-9 receive the input,
compute the answer, and print it:
hours = int( raw_input("Please type an hours amount, a nonnegative int: "))
minutes = hours * 60
print "The number of minutes is", minutes, "."
Note that
You should experiment with this script: Try it with different inputs (say, 660 or 0 or -12 or Help!). Next, edit the file HoursToMinutes.py and alter its commands: add spaces or remove them; add blank lines or remove them; place comments in new places. Also, remove the commas in Line 9 and see what happens when you use the script. Change the name, hours to HOURS or fred or hours12 or 12hours.
Some of these changes will cause the script to misbehave; others won't. Look at the error messages that result from using a badly written script. These experiments are exposing the meaning of semantics of the fundamental Python commands.
Here is the conversion of Celsius temperatures to Fahrenheit,
written as a program:
=============================
# CtoF
# Converts Celsius to Fahrenheit
# assumed input: celsius - an integer (whole number)
# guaranteed output: the corresponding amount in fahrenheit degrees
celsius = int(raw_input("Type Celsius degrees, an int: "))
fahrenheit = ((9.0/5.0) * celsius) + 32.0 # note the fractions!
print "The corresponding temperature in Fahrenheit is", fahrenheit
raw_input("\n\npress Enter to finish")
===================================
You can test it:
$python CtoF
Type Celsius degrees, an int: 22
The corresponding temperature in Fahrenheit is 71.599999999999994
dollars = 49 cents = 95 print "$", dollars, ".", centsThis prints
$ 49 . 95For better or for worse, the extra spaces appear. There is a trick to eliminate the spaces: The Python operation, str, converts a number to a string, so that the string can be appended to another string without any intervening spaces. Try this:
dollars = 49 cents = 95 print "$" + str(dollars) + "." + str(cents)This prints
$49.95because its appends together "$" + "49" + "." + "95".
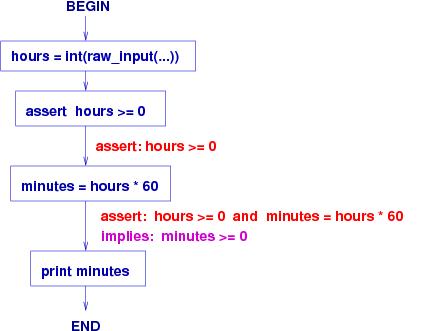
Consider again the program that converts hours into minutes.
It is shown here with the assertions that indicate
the knowledge generated in the course of the computation:
=====================================================
# HoursToMinutes
# This program converts hours to minutes.
# assumed input: hours - a nonnegative integer
# guaranteed output: the conversion of hours to the corresponding amount
# of minutes, a nonnegative integer
hours = int( raw_input("Please type an hours amount, a nonnegative int: "))
# assert: hours >= 0 ( >= means ``greater-than-or-equals'')
minutes = hours * 60
# assert: hours >=0 and minutes = hours * 60
# implies: minutes >= 0
print "The number of minutes is " + str(minutes) + "."
raw_input("\n\npress Enter to finish")
========================================================
Our analysis of the program's computation shows that the
minutes that are printed are indeed a nonnegative integer,
provided that the input is a nonnegative integer.
As we well know, people often fail to read instructions, and
there might well be someone who tries something silly, like this:
$ python HoursToMinutes.py
Please type an hours amount, a nonnegative int: -6
The number of minutes is -240.
The output is inappropriate (``garbage'') because the input was
garbage.
The Python language lets us insert an assertion into a program
and enforce it as a safety check while the program computes.
We do it like this:
FIGURE==================================================
hours = int( raw_input("Please type an hours amount, a nonnegative int: "))
assert hours >= 0 # this assert will be checked while the program executes!
minutes = hours * 60
print "The number of minutes is " + str(minutes) + "."
raw_input("\n\npress Enter to finish")
ENDFIGURE==================================================
The command,
assert hours >= 0
is checked by the computer immediately after the hours are received.
If the value assigned to hours is indeed nonnegative,
the program proceeds as intended with no interruption.
But if hours's value is negative,
the program halts with an assertion error.
Here is a example of an assertion error:
$ python HoursToMinutes.py
Please type an hours amount, a nonnegative int: -6
Traceback (most recent call last):
File "HoursToMinutes.py", line 4, in ?
assert hours >= 0 # this assert will be checked while the program executes!
AssertionError
It is a good idea to insert assert commands when the
correct behavior of the program depends on correct input values.
It is unnecessary (but causes no harm) to add additional asserts:
=========================================================
hours = int( raw_input("Please type an hours amount, a nonnegative int: "))
assert hours >= 0
minutes = hours * 60
assert hours >=0 and minutes == hours * 60 # note that == means ``equals''
assert minutes >= 0
print "The number of minutes is " + str(minutes) + "."
===========================================================
The additional asserts are unncessary because our algebraic calculations
guarantee that, if the input is nonnegative, the remainder of the
program behaves correctly.
In practice, a software engineer might not have adequate time to calculate the precise knowledge generated at all key places within a huge program. In this situation, the software engineer inserts assert commands to monitor and verify that the program is operating with appropriate knowledge at the key places. We will use assert commands in this way in later examples in these notes.
When you first start your computer, it looks like this:
The start-up program, the operating system (OS), rests in primary storage,
and the CPU reads and does the instructions of the OS. (The instructions
are commands like, ``redraw the pictures on the display,'' ``see what
that mouse click is about,'' ``make the clock move forward by one second,''
and so on.)
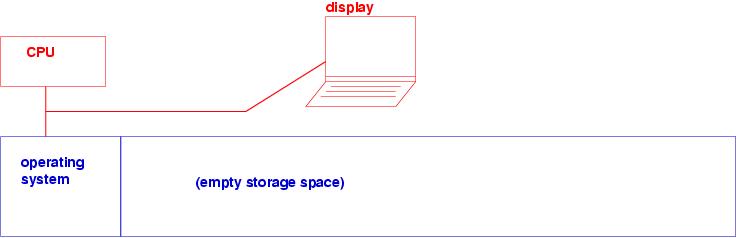
Say that you start a python program; the OS reads your request and tells the CPU to do these steps:
Notice that the Python interpreter has a variable of its own --- the instruction counter (i.c.), which remembers which line of the Python program must be executed next.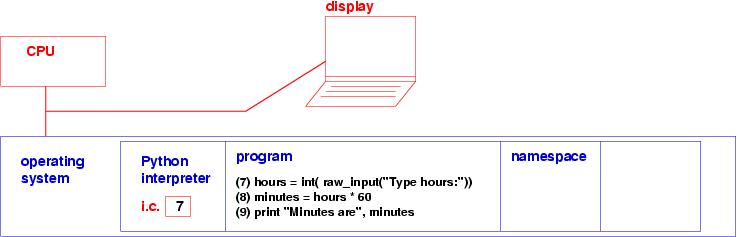
Let's follow the semantics of the example program. Line 7 is
hours = int( raw_input("Please type an hours amount, a nonnegative int: "))
To execute the assignment, the Python interpreter triggers these steps:
Line 8 computes the assignment,
minutes = hours * 60
which creates a second variable
cell in the namespace:
Next, the phrase, hours * 60 is computed: The name, hours,
is located in the namespace, and the number in its cell is extracted:
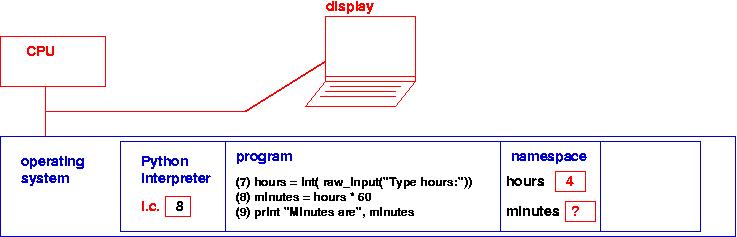
Next, the arithmetic is calculated, and the answer is stored into the
cell named hours:
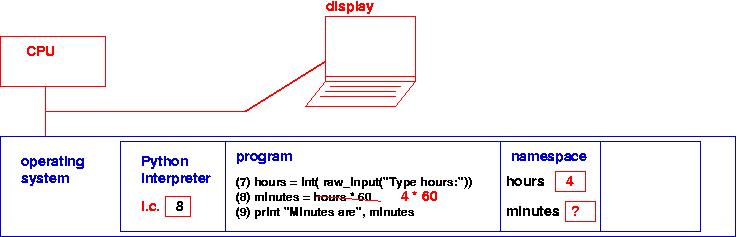
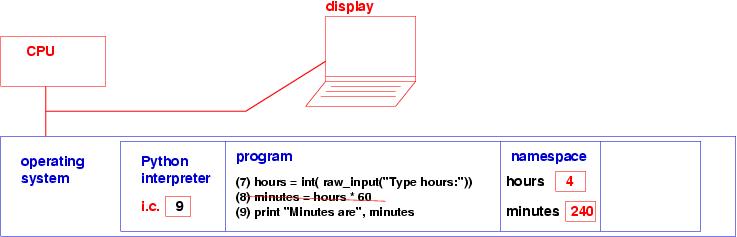
Finally,
print "Minutes are", minutes
looks at the value of minutes in the namespace and displays
it:
Notice that print is itself another function, whose job
is to compute some text and display it. print's argument
comes immediately after the word, print, and there is no
need for matching parentheses. (Sorry for this inconsistency ---
usually a function's argument is bracketed by parentheses.)

Now, the above pictures look different from the ones we saw in the chapter about Computer Architecture --- where are the computer words that were mentioned in the earlier chapter? The answer is that the OS instructions are copied into some computer words, and the instructions of the Python interpreter are copies into some computer words, and the Python interpreter's instruction counter (i.c.) is itself a number that is copied into a computer word.
The Python program is copied into some computer words, and the namespace is a large area of empty computer words. When a variable is assigned, like hours = 4, one computer word holds the name, hours, and one computer word holds the integer, 4. So, the ``cells'' mentioned in the above explanation are computer words.
Now that we know how variables and their values are remembered in
computer storage, we can study
tricky sequences of commands.
First, what if the previous example program was modified to look
like this:
hours = 4
minutes = hours * 60
print minutes
hours = 5
minutes = hours * 60
print minutes
We know that the program should print 240 and then 300,
but now we can understand why: after the cell named hours
is set to 4 and minutes's cell is set to 240 and printed,
we have this namespace:
hours = 4
minutes = hours * 60
print minutes
The fourth command destroys the value in hours's cell, replacing it
by 5:

hours = 5
The fifth command computes hours * 60 and placed the answer
in minutes's cell, destroying the old value:

minutes = hours * 60
The example shows that an assignment command always places a value
in a variable's cell, destroying what was there before. In this
sense, assignment commands are different from algebraic equations,
where there is no notion of ``changing'' the value of a variable.

Here is a second example:
x = 2
x = x + 1
When the program starts, the
namespace is empty:
x = 2
x = x + 1
When x = 2 is computed, a cell is created for x:

x = 2
and then 2 is stored in it:
 x = x + 1
x = x + 1
x = 2
(Notice how the namespace holds the generated knowledge.)
 # assert: x = 2
x = x + 1
# assert: x = 2
x = x + 1
Next, the command
x = x + 1 begins by checking if there is a cell for
the variable on the left-hand side, x. (There is.)
Next, the expression x+1 computes to 3, and 3 is inserted into
x's cell:
x = 2
x = x + 1
The example shows how the namespace uses the ``old'' value of a variable
to generate a ``new'' one ---
the assignment resets the value in the cell in the namespace.
 # assert: x_old = 2 and x_new = x_old + 1
# implies: x_new = 3
# implies: x = 3
# assert: x_old = 2 and x_new = x_old + 1
# implies: x_new = 3
# implies: x = 3
Here is another example. Say we have a program with just this one command:
x = x + 1
As before, the namespace starts empty:
x = x + 1
and the assignment statement executes. First, since there is no
cell for x, one is created in the namespace:

x = x + 1
Next, x + 1 is computed. But when the value for x
is fetched, nothing is found in the cell. The Python interpreter
prints this error message and halts:

>>> x = x + 1
Traceback (most recent call last):
File "
Our careful reading of the semantics of assignment shows us that a
variable cannot be used in an expression if it does not already have
a value in its cell in the namespace.
Writing a program's execution trace is the best way of understanding what the program does. This is not only useful for understanding a program someone else has written, but also for checking your own programming work and explaining it to others.
A quick way of writing an execution trace starts like this:
hours = int( raw_input("Please type an hours amount: ")) #7
minutes = hours * 60 #8
print "The number of minutes is", minutes, "." #9
Our sheet of paper is grouped into three columns, like this:
i.c. namespace display -----+-------------------+--------- 7 | |We ``play computer'' and execute command 7:
i.c. namespace display -----+-------------------+--------- X7 | hours : 4 | Please type an hours amount: 4 8We have recorded that a message appeared on the display, the human typed input 4, and a variable named hours was constructed in the namespace. The next command is at line 8. When we execute it, the execution trace is modified to this:
i.c. namespace display -----+-------------------+--------- X7 | hours : 4 | Please type an hours amount: 4 X8 | minutes : 240 | 9 |and after command 9 finishes, we are done:
i.c. namespace display -----+-------------------+--------- X7 | hours : 4 | Please type an hours amount: 4 X8 | minutes : 240 | X9 | | The number of minutes is 240 .Computer traces will be valuable to us in the near future.
Floats (fractional numbers) can be inputs and outputs.
For practice, study and use this script:
=============================
# CtoF
# Converts Celsius to Fahrenheit
# assumed input: celsius - a fractional number
# guaranteed output: the corresponding amount in fahrenheit degrees
celsius = float( raw_input("Type Celsius degrees, a fraction: "))
fahrenheit = ((9.0/5.0) * celsius) + 32.0 # note the fractions!
print "The corresponding temperature in Fahrenheit is", fahrenheit
raw_input("\n\npress Enter to finish")
===================================
This program looks lots like the ones seen earlier; the only
new idea is the conversion operator, float( .... ),
which makes a string that looks like a fractional number into a
float.
We can test it:
$python CtoF
Type Celsius degrees, a fraction: 20.2
The corresponding temperature in Fahrenheit is 68.36
The recipe is an algorithm --- a sequence of commands that accomplish a goal. Algorithms are also used in computing:
Algorithms often follow a standard pattern or format. For example, the standard algorithmic pattern we have used in this lecture goes like this:
Also, a text editor or a spreadsheet program uses the standard algorithmic pattern, and the key idea is that it uses the pattern over and over again, each time the user inserts a new number into a cell of the spreadsheet or the user inserts a new line of text into the edited document.
For example, if you practice converting celsius temperatures to fahrenheit temperatures often enough, you will learn the correct pattern of arithmetic and you will be able to explain it to someone else (or a computer).
We cannot write a program in English words and pictures; we must use a programming language, like Python, which forces us to ``talk'' in a stilted way. It is difficult to explain our ideas correctly in a programming language, but there is a standard list of steps that we can follow that leads us to writing correct programs:
Let's consider each stage within an example.
Stage 1. describe behavior: Say that you want a program that adds up the value of the coins in your pocket.
How would you add the coins in your pocket? If you practice this awhile, you quickly learn that you total the quarters, add to this the total of the dimes, then the nickels, then the pennies. Now, you must explain to the computer the technique you practiced and learned.
You begin by asking how the computer will behave when someone
asks it to add up some coins.
For the change-making program, we might expect the computer to
interact with the human like this:
How many quarters? (you type here, say, 9)
How many dimes? (you type, say, 3)
How many nickels? (you type, say, 0)
How many pennies? (you type 212)
The total is 4 dollars and 67 cents.
Have a nice day.
This one example of the computer doing the job is called a
scenario or use-case.
You should plan out several of these scenarios that show
how the computer should act.
Once you have these, you can start planning the steps
the computer takes to
generate the behaviors in the scenarios.
Stage 2. design the algorithm: Now, we write in English the steps that generate the desired behavior. The steps are just an algorithm. Here is the pattern of algorithm we saw a bit earlier:
quarters = read "How many quarters? " dimes = read "How many dimes? " nickels = read "How many nickels? " pennies = read "How many pennies? "
total = quarters * 25 + dimes * 10 + nickels * 5 + pennies * 1 dollars = total / 100 # remember that int division forgets the fraction ! cents = total % 100 # remember that int modulo keeps the remainder !
print "The total is", dollars, "and", cents
Stage 3. write and test:
Now we make the
refined algorithm into a Python program ---
There should be enough details listed
that we need not think too hard at this point!
Here is what we have:
=======================
# Total
# computes the dollars-cents value of a collection of U.S. coins.
quarters = int(raw_input("How many quarters? "))
dimes = int(raw_input("How many dimes? "))
nickels = int(raw_input("How many nickels? "))
pennies = int(raw_input("How many pennies? "))
total = (quarters * 25) + (dimes * 10) + (nickels * 5) + (pennies * 1)
dollars = total / 100 # integer division forgets the fraction
cents = total % 100 # modulo keeps the remainder
print "The total is", dollars, "and", cents
raw_input("\n\nHave a nice day.")
==============================
You should test the
program with the behaviors you wrote in Stage 1 as well as with
a variety of reasonable and silly input values.
(For example, what happens if your program receives -24 nickels ? Or,
3.6 quarters ? Are you happy with the program's outputs for these
cases, or do you wish to make some assumptions about the
inputs that are reasonable ?)
Don't forget to write an execution trace or two, if you do not understand the behaviors you see produced by the computer for your program!
Stage 4. document:
Finally, write the commentary that appears in every program:
List the program's name, its purpose, input assumptions,
and guarantees of correct output. For the change program, we might
write this:
# Total
# computes the dollars-cents value of a collection of U.S. coins.
# assumed inputs:
# the quantity of quarter coins, a nonnegative int
# the quantity of dime coins, a nonnegative int
# the quantity of nickel coins, a nonnegative int
# the quantity of pennies, a nonnegative int
# guaranteed output: the total value of the coins, stated in dollars and cents
The documentation makes clear that the input numbers should
be nonnegative integers (because it would be ridiculous to compute
the monetary value of some ``negative'' quantity of coins).
The demands on the inputs generate assertions that we can add
to the program. We should also perform the necessary algebra
to prove that the guaranteed output will be as expected.
Here is the complete, documented, analyzed program:
FIGURE===============================================
# Total
# computes the dollars-cents value of a collection of U.S. coins.
# assumed inputs:
# the quantity of quarter coins, a nonnegative int
# the quantity of dime coins, a nonnegative int
# the quantity of nickel coins, a nonnegative int
# the quantity of pennies, a nonnegative int
# guaranteed output: the total value of the coins, stated in dollars and cents
quarters = int(raw_input("How many quarters? "))
dimes = int(raw_input("How many dimes? "))
nickels = int(raw_input("How many nickels? "))
pennies = int(raw_input("How many pennies? "))
assert quarters >= 0 and dimes >= 0 and nickels >=0 and pennies >= 0
total = (quarters * 25) + (dimes * 10) + (nickels * 5) + (pennies * 1)
dollars = total / 100 # integer division forgets the fraction
cents = total % 100 # modulo keeps the remainder
#! assert: total >= 0 and total = (dollars * 100) + cents
print "The total is", dollars, "and", cents
raw_input("\n\nHave a nice day.")
ENDFIGURE=================================================
The Python assert command protects the program so that it is
not forced to compute on bad inputs. The usual calculations
produce this knowledge at the place labelled #!:
quarters >= 0 and dimes >= 0 and nickels >=0 and pennies >= 0
total = (quarters * 25) + (dimes * 10) + (nickels * 5) + (pennies * 1)
dollars = total / 100
cents = total % 100
Applying algebra, we quickly calculate that
total >= 0
and that
total = (dollars * 100) + cents
which verifies that we have printed the correct dollars-and-cents numbers
for the input.
If you practice now the steps of program development given here, you will find it easier to design interesting, correctly working programs.
printt "the end"or use punctuation or parentheses incorrectly:
x = (2 + 1))When the Python interpreter reads such a command, it will reply with an error message, and often the message is a bit difficult to understand. Here is an example, shown to you as a warning:
hours = int( raw_input("Type hours, an int: ")
minutes = hours * 60
(Notice the missing right bracket in the first line.)
When this script is executed, there is a surprising reply:
$ python Error.py
File "Error.py", line 2
minutes = hours * 60
^
SyntaxError: invalid syntax
Of course, there is nothing wrong with line 2 --- it's line 1 that hasn't
ended properly ! So, don't hesitate to look at the lines just before
an error message as well as the line that is supposedly erroneous.
hours = int( raw_input("Type hours, an int: "))
minutes = hour * 60
and when we test the script, we see this:
$ python Error.py
Type hours, an int: 4
Traceback (most recent call last):
File "Error.py", line 3, in ?
minutes = hour * 60
NameError: name 'hour' is not defined
The interpreter notices that we have mistakenly used hour
instead of hours on line 3.
But other errors cannot be noticed by the Python interpreter. Again,
we are converting hours to minutes and type
minutes = hours + 60
there is no way that the Python interpreter can identify the incorrect
use of +. This is why we must write multiple scenarios and
test the program with the scenarios.
It is easy to start a Python program --- double-click on its icon. But if the program contains an error, then the error message will flash onto the display and disappear almost immediately!
It is better to test a new Python program by starting it within a command window:
This starts your program and makes the program show its work in the opened command-prompt window. If there is an error, the error message will appear in the window.
A Python PROGRAM is a sequence of COMMANDs, one per line. The COMMANDs are executed one after the other.
A COMMAND can be
VARIABLE = EXPRESSIONEXAMPLES: minutes = hours * 60 and hours = int(raw_input("Type an int: "))
The semantics of an assignment goes in two steps:
print EXPRESSION_COMMASwhere EXPRESSION_COMMAS is a sequence of expressions separated by commas. EXAMPLE: print "minutes are", (hours * 60), "."
The semantics is that
assert COMPARISON_EXPRESSIONwhere COMPARISON_EXPRESSION, as used in this chapter, is a sequence of arithmetic-expression comparisons, separated by the keyword, and. EXAMPLE: assert hours > 0 and minutes == hours * 60.
There are many possible forms of EXPRESSION:
A Python program has a meaning (semantics): When a program is started, it is copied into computer storage, along with the Python interpreter and an empty namespace. The Python interpreter reads the program's commands, one by one, and tells the CPU what to do to compute the commands. The program's variables are constructed in the namespace.
A program should be designed, written, and tested in stages:
Say that you want a shortcut for a program, Pgm.py, which is saved in the folder, C:\MyPython:
The shortcut icon is actually these
commands, which execute when you double click on the icon:
set path=C:\Python22
cd C:\MyPython
python Pgm.py
You can read the program and edit it by right-clicking on the icon,
selecting OpenWith and selecting Notepad.