These questions are studied within computational complexity theory. We learn about this topic by studying some simple algorithms that work with arrays.
Step 1: V
[6, 10, 2, 4, 12, 16, 8, 14]
Step 2: V
[6, 10, 2, 4, 12, 16, 8, 14]
...
Step 7: V
[6, 10, 2, 4, 12, 16, 8, 14]
We search the array from front to back. How fast is this algorithm?
Without worrying about speeds of chips, we measure the speed of an
array algorithm by how many array lookups/updates it must do.
Obviously, with an array of length 8, at most 8 lookups is needed; in general, if the array has length N, at most N lookups is needed. This is the worst-cast time complexity, and in this case is linearly proportional to the length of the array. We say that sequential search is a linear-time algorithm, that is, of order-N.
Here is a table of how a linear-time algorithm performs:
array size, N worst-case time complexity, in terms of lookups ---------------------------------------------- 64 64 512 512 10,000 10,000A linear-time algorithm looks "slow" to its user but is tolerable if the data structure is not "too large".
When you write a one-loop program that counts through the elements of an array, your algorithm runs in linear time.
Find 8 in [2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22]:
Step 1: look in middle: V
[2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22]
Step 2: look in middle of left half: V
[2, 4, 6, 8, 10 ... ]
Step 3: look in middle of left's right subhalf: V
[ ..., 8, 10, ... ]
The subarray searched shrinks by half each time there is a
lookup, and the key is quickly found --- in worst case,
at most log2N lookups are needed to find the key. (Recall that
log2N = M
means that 2M = N.)
This is log-time, that is, of order log-N.
Here's a table:
array size, N linear-time log-time ---------------------------------------------- 64 64 6 512 512 8 10,000 10,000 12The speed-up is spectacular; this algorithm is markedly faster in theory and in practice. In practice, regardless of how a database is configured, the search operation must be order log-time or faster --- when you do a search on a web site, the computer program that does the searching is order log-time.
When you write an algorithm that "discards" half of a data structure during each processing step, you are writing a log-time algorithm.
SELECTION SORT: Input array Output array --------------------------- -------------------- [6, 10, 2, 4, 12, 16, 8, 14] [] [6, 10, 4, 12, 16, 8, 14] [2] [6, 10, 12, 16, 8, 14] [2, 4] [10, 12, 16, 8, 14] [2, 4, 6] . . . [16] [2, 4, 6, 8, 10, 12, 14] [] [2, 4, 6, 8, 10, 12, 14, 16]The algorithm scans the N-element input array N-1 times, and 1/2(N2 - N) lookups are done; there are also N updates to the output array. This is a quadratic-time algorithm, order N2. Here is the comparison table:
array size, N linear log2N N2 1/2(N2 + N) ------------------------------------------------------- 64 64 6 4096 2064 512 512 8 262,144 131,200 10,000 10,000 12 100,000,000 50,002,500(Note there isn't a gross difference between the numbers in the last two columns. That's why selection sort is called a quadratic-time algorithm.)
A quadratic-time algorithm runs slowly for even small data structures. It cannot be used for any interactive system --- you run this kind of algorithm while you go to lunch. When you write a loop-in-a-loop to process an array, you are writing a quadratic algorithm.
The standard sorting algorithms are quadratic-time, but there is a clever version of sorting, called "quicksort", that is based on a divide-and-conquer strategy, using a kind of binary search to replace one of the nested loops in the standard sorting algorithms. Quicksort runs in order N * log2N time:
N log2N N2 N*log2N ------------------------------------------------------- 64 6 4096 384 512 8 262,144 4096 10,000 12 100,000,000 120,000

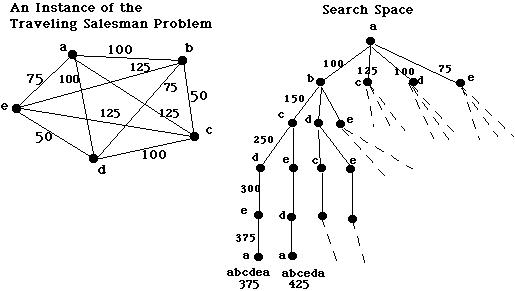
These problems require that you calculate all possible combinations of a data structure before you select the best one. Many important industrial and scientific problems, which ask for optimal solutions to complex constraints, are just the problems stated here.
The problems stated above are solvable --- indeed, here is a Python function that calculates all the permutations (shuffles) of a deck of size-many cards:
def permutations(size) :
"""computes a list of all permutations of [1,2,..upto..,size]
param: size, a nonnegative int
returns: answer, a list of all the permutations defined above
"""
assert size >= 0
if size == 0 :
answer = [[]] # there is only the "empty permutation" of a size-0 deck
else :
sublist = permutations(size - 1) # compute perms of [1,..upto..,size-1]
answer = [] # build the answer for size-many cards in a deck
for perm in sublist:
# insert size in all possible positions of each perm:
for i in range(len(perm)+1) :
answer.append( perm[:i] + [size] + perm[i:] )
return answer
It uses a recursion and a nested loop. For example,
permutations(3) computes
[[3, 2, 1], [2, 3, 1], [2, 1, 3], [3, 1, 2], [1, 3, 2], [1, 2, 3]].
Try this function on your computer and see how large an argument you
can supply until the computer refuses to respond.
The solution to the above is written in just a few lines of Prolog, which is an ideal language for calculating all combinations that satisfy a set of constraints:
/* permutation(Xs, Zs) holds true if list Zs is a reordering of list Xs */ permutation([], []). permutation(Xs, [Z|Zs]) :- select(Z, Xs, Ys), permutation(Ys, Zs). /* select(X, HasAnX, HasOneLessX) "extracts" X from HasAnX, giving HasOneLessX. It's a built-in Prolog operation, but here's the code: */ select(X, [X|Rest], Rest). select(X, [Y|Ys], [Y|Zs]) :- select(X, Ys, Zs). /* This query computes all the permutations and saves them in Answer: */ ?- findall(Perm, permutations([0,1,2,...,size], Perm), Answer).
One way of sorting a deck of cards is by computing all the shuffles (permutations) and keeping the one that places the cards in order. But this strategy will be very slow! How slow?
Permutation problems, like all-N-shuffles and travelling-salesman-to-N-cities, require 1*2*3*..upto..*N data-structure lookups/updates to compute their answers. This number is abbreviated as N!, called factorial N, and it grows huge quickly:
N log2N N2 N*log2N N! ------------------------------------------------------- 64 6 4096 384 126886932185884164103433389335161480802865516174545192198801894375214704230400000000000000 512 8 262,144 4096 347728979313260536328304591754560471199225065564351457034247483155161041206635254347320985033950225364432243311021394545295001702070069013264153113260937941358711864044716186861040899557497361427588282356254968425012480396855239725120562512065555822121708786443620799246550959187232026838081415178588172535280020786313470076859739980965720873849904291373826841584712798618430387338042329771801724767691095019545758986942732515033551529595009876999279553931070378592917099002397061907147143424113252117585950817850896618433994140232823316432187410356341262386332496954319973130407342567282027398579382543048456876800862349928140411905431276197435674603281842530744177527365885721629512253872386613118821540847897493107398381956081763695236422795880296204301770808809477147632428639299038833046264585834888158847387737841843413664892833586209196366979775748895821826924040057845140287522238675082137570315954526727437094904914796782641000740777897919134093393530422760955140211387173650047358347353379234387609261306673773281412893026941927424000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 10,000 12 100,000,000 120,000 ????????????????????????????????????????????????????????????????????????????????No computer, no matter how fast, can use an algorithm that requires factorial time. A problem that has no faster solution than this is called intractable --- unsolvable in practice.
There is a way to improve the performance of permutation problems: remember partial solutions and reuse them over and over. You can do this in the travelling-salesman problem, where the distances over subpaths in the graph can be saved in a table and reused as often as possible when computing longer paths. (This technique is called dynamic programming.) The resulting algorithm uses about 2N lookups --- exponential time:
N log2N N2 N*log2N 2N ------------------------------------------------------- 64 6 4096 384 18446744073709551616 512 8 262,144 4096 13407807929942597099574024998205846127479365820592393377723561443721764030073546976801874298166903427690031858186486050853753882811946569946433649006084096 10,000 12 100,000,000 120,000 ????????????????????????????????????????????????????????????????????????????????Exponential-time algorithms are still too slow to use in practice. At best, you start one and come back in a day. (I am not kidding; people do this.)
Computational complexity theory is the study of the fundamental time and space requirements for solving important problems.
Finish this exercise as follows:
How far did you progress with your experiments until your computer failed to respond? Is the computer lost? tired? worn out? What if you bought a new computer that is twice as fast or even ten times as fast as the one you are now using --- would it help here? Is it realistic to compute all the permutations of an ordinary 52-card deck of cards so that you can prepare for your next trip to Las Vegas? Can't computers do things like this?
sortList(nums) :
"""sortList finds the sorted permutation of int list nums by brute force"""
allindexpermutations = permutations(len(nums))
for indexperm in allindexpermutations :
possibleanswer = []
for i in indexperm :
possibleanswer = possibleanswer.append(nums[i-1])
print "Possible sorted version is", possibleanswer
if isOrdered(possibleanswer) :
print "Found it!"
return possibleanswer
Find a better way of sorting a list of ints.