Computers do calculation activities. They calculate on numbers (represented as 1s and 0s), on text (represented as numbers), on sounds (represented as numbers), on images (represented as numbers), etc. Are there some calculation activities that are beyond the reach of computers, that they cannot do? The answer is "yes".
MacCormick demonstrates this point with a complex presentation of Turing's Halting Problem. We will rework that material here.
So does Western Thought. A sentence can be an imperative (e.g., "Do your homework!"), a question ("Are we there yet?"), or a declaration ("The sky is blue.") Here, we care about declarations. The declaration, "The earth is round" is a fact; it says something; it is True; it is 1. The declaration, "The moon is made of green cheese" is a falsehood; it says nothing; it is False; it is 0.
The oldest known example of a paradox is the sentence, "I am lying." --- the declaration is a fact exactly when it is a falsehood (since "lying" means "stating a falsehood"). This is the Liar's Paradox. An alternative formulation is "This declaration is a falsehood". The Liar's Paradox is nonsensical; it cannot be.
Paradoxes have infiltrated mathematics. Declarations in mathematics are called predicates; here are examples:
Mathematicians has always worked with numbers, but in the nineteenth century, mathematicians started using predicates to define sets. (Recall that a "set" is a collection --- a "grocery sack" --- of elements. Examples: {4,5,6} is a set of some numbers. {} is a set of no numbers.)
Here are examples of sets of numbers, defined with predicates. (Read the first one as, ''the set of elements, n, such that n > 0 is a fact.'')
A predicate that mentions variable x, call it Px,
defines the set, {x | Px}
For example, n > 0 is a predicate that mentions variable n and it defines the set of positive numbers, {n | n > 0}.
The whole point of defining a set is to ask what's in it. The predicate, e ∈ S, is a fact exactly when element e is contained in set S. (Read as "e is in S".) For example, 5 ∈ {4,5,6} is a fact. When a set is defined via a predicate,
e ∈ {x | Px} is a fact exactly when we replace x in Px with e and we find that Pe is a fact.
For example, 3 ∈ {n | n > 0} is a fact because, when we replace n in n > 0 by 3, we find that 3 > 0 is a fact.
Similarly, 3 ∈ {m | not(m + m = 0)} is a fact because not(3 + 3 = 0) is a fact.
Finally, 3 ∈ {m | m + m = 0} is a falsehood because
3 + 3 = 0 is a falsehood.
Mathematicians use sets to hold sets. Here are examples:
RUSSELL'S PARADOX:
Let R be {S | not(S ∈ S)}
↑
R ∈ R ↑
is a fact exactly when not(R ∈ R)
is a fact, that is, exactly when R ∈ R is a falsehood
R ∈ R is a paradox!
Russell's Paradox is generated by the combination of S ∈ S (self-inspection) and
not ("flipping" the answer) --- a real
disaster!
We have uncovered something that mathematics cannot do --- define a set of sets that don't hold themselves. Modern versions of set theory essentially disallow self-inspection to remove this form of paradox.
In modern set theory, numbers like 0,1,2,... are themselves sets:
That is, a human loaded and started WIN-WORD.EXE on the computer's processor, and the human told the running program to load as the input, WIN-WORD.EXE.
Editor programs, like MS Word, are capable of inspecting all programs, including themselves. Compiler/interpreter/IDE programs are capable of inspecting/compiling/running most all programs, including themselves. Error-finding and performance-analyzing and correctness-checking programs are capable of inspecting/analyzing a wide range of programs, including themselves. A key feature of computer programs, one that leads us into artificial-intelligence-like areas, is that they are capable of inspecting other programs, including themselves.
How far can these inspections go?
The computer processor does the calculations stated in the program. If all goes well, the program converges (halts, terminates) and emits an output, a number. If something goes wrong and no output is emitted, the program diverges (loops, freezes, goes lost, runs forever, hangs).
We will write requirements for programs rather precisely, in a set-like format, { input |-> output ... }, to define how a program should transform its input into its output. The output can be either of ↓answer (converges and emits answer) or ↑ (diverges).
Here are some examples:
{ n |-> ↓(n * n) }
It is easy to implement this requirement with a program that obtains its input number n, multiplies it by itself, then emits the output number:
INPUT: a number, n
OUTPUT: a number
ALGORITHM: 1. obtain n and calculate answer = n * n
2. output answer
Say that the program we write is named square. We say
{ n |-> ↓m iff m * m = n
|-> ↑ iff there is no m such that m * m = n }
Note: iff means "exactly when"
This requirement might be implemented by a program that obtains its input and guesses possible answers (0,1,2, etc.) until an output,
m is found, if ever. (If not, the program runs forever.)
Say that sqrt is the name of the program we built as just described. Here are two uses of it: run(sqrt)(25)↓5; run(sqrt)(7)↑.
{ b,e |-> ↓(b*b*...*b), repeated e times, iff e > 0
|-> ↓1 iff e = 0 }
If exp is a program that implements the specification,
then we have run(exp)(2,4)↓16 and
run(exp)(3,0)↓1.
The situation in computing is looking like the one in mathematics. We must be alert for paradoxes.
{n |-> ↓1 iff (n * n) > n }
Write an algorithm for this requirement, anyway. What does the algorithm do for those inputs not covered by the above requirement?
{ n |-> ↓0 iff (n + n) = n
|-> ↓1 iff (n * n) = n
|-> ↑ iff neither of the above two cases apply to n }
Modify the requirement so that there is an implementation.
{ p |-> ↓(a + 1) iff run(p)(0)↓a
|-> ↑ iff run(p)(0)↑ }
The requirement asks that we run input number/program p with datum 0 and add one to its answer, if there is one.
There is an easy algorithm that does this:
INPUT: a program, p, coded as an integer OUTPUT: a number or ↑ ALGORITHM: 1. do run(p)(0) and wait.... 2. if run(p)(0)↓a, then produce output a+1 (if run(p)(0)↑, then we are still waiting, and there is nothing we can do)
Not all such requirements can be implemented. In particular, we can restate Russell's paradox as this requirement:
RUSSELL'S PARADOX REPHRASED AS A REQUIREMENT:
{ p |-> ↓1 iff run(p)(p)↑
|-> ↑ iff run(p)(p)↓answer }
If some program, named Russell, implemented this requirement, then
run(Russell)(Russell)↓answer iff run(Russell)(Russell)↑
which cannot be.
Notice how the specification uses self-inspection (run(p)(p)) and then "flips" the answer --- in particular, ↑ is flipped to ↓1, which goes against
intuition. (How can a computer program ever know that another computer program "has gone lost"?)
It is not surprising that the above requirement can never become a program, but its consequences are many. In particular, there is an incredibly useful program that we can now prove is impossible to implement:
TURING'S HALTING PROBLEM:
Is it possible to implement a program that can analyze another
program and its input and predict in advance
whether the program and input will halt (converge to an answer)?
{ p,d |-> ↓1 iff run(p)(d)↓answer
|-> ↓0 iff run(p)(d)↑ }
Unfortunately, the answer is no:
If some program, named Turing, implemented the above requirement, then we could build the Russell program, like this: INPUT: a program, p, coded as an integer OUTPUT: ↓1 or ↑ ALGORITHM: 1. run(Turing)(p,p) and obtain the output answer, which must be 0 or 1 2. if answer = ↓1 then diverge: ↑ if answer = ↓0 then produce output ↓1 This generates an implementation of Russell's paradox, which cannot be.The halting problem states a requirement that can never be implemented by a computer program. Many other requirements are also impossible to implement:
In practice, there are still text-editor, analyzer, and error-finding programs that can examine other programs, even themselves. But they cannot answer all the interesting questions about programs that we might like them to answer. For difficult requirements, such as the halting program, the best one might do is build a program that converges to a useful answer some of the time, like the sqrt program seen earlier does, and diverges lots of other times (because the program cannot discover an answer and "goes lost".)
Computing is "constructive mathematics," and since mathematics has its limitations, so does computing.
{ p |-> ↓1 iff for each input, n, there is some m such that run(p)(n)↓m
|-> ↓0 iff there is some k such that run(p(k)↑ }
( p,q |-> ↓1 iff for all inputs, n, run(p)(n) = run(q)(n)
|-> ↓0 iff there is some k such that run(p)(k) ≠ run(q)(k) }
{ p,d |-> ↓1 iff p ≠ d and run(p)(d)↓answer
|-> ↓0 iff p ≠ d and run(p)(d)↑
|-> ↑ iff p = d }
That is, we don't try to answer if we are asked
the outcome of run(p)(p). Why is the above
requirement still impossible to implement? (Hint: consider the second requirement in the previous question!)
Turing was interested in mathematical games and machines for calculation. His Turing machine was a controller with a read-write head that traversed the squares of an unbounded roll of toilet paper, where only a 0 or a 1 can be written in a square:
Turing realized that the controller could be wired as a "processor" that understood these six instructions:
* move Left/Right one square * erase the square (make it blank) * write 0/1 on the square * if square is blank/0/1, then goto Instruction #n * goto Instruction #n * stopHere is a sample program that scans a binary number from left to right and flips all 0s to 1s and all 1s to 0s:
#1: if square is 0, then goto #4 #2: if square is 1, then goto #6 #3: if square is blank, then goto #9 #4: write 1 #5: goto #7 #6: write 0 #7: move Right #8: goto #1 #9: stopThe nine instructions have number codings, and the program can be copied onto a tape as one huge (Base-2) number to be read by the controller. The Universal Turing Machine was configured like this:... => ...

The Universal Turing Machine is the origin of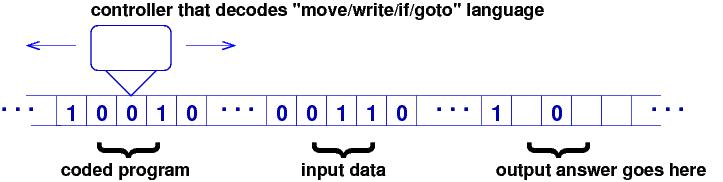
Turing wrote programs for the Universal Turing machine, and he believed that all facts/knowledge/problems that can be calculated/deduced/solved by a machine can be done by a Universal Turing Machine. This is now known as the Church-Turing thesis. (The "Church" part refers to Alonzo Church, a Princeton mathematician who developed a symbol system, the lambda-calculus, which has the same computational powers as Turing's machines.)
Turing asked: Are there some problems whose solutions cannot be calculated by his machine? This led to his formulation of the Halting Problem, which was developed earlier in this note.
The first electronic computers were "non universal" machines, where the computer program was wired into the CPU. The wires were moved around when a new program was desired. The ENIAC people implemented Turing's machine language, stored programs, and "universal" CPUs. That basic architecture, the von Neumann computer architecture, has survived to this day, because it is simple, relatively cheap to manufacture, and satisfies the Church-Turing thesis.
V
| |1|0|1|1| | and it moves to the right of the int,
till it finds the rightmost digit:
V
| |1|0|1|1| | Then it adds one and does the needed carries
until it is finished:
V V
| |1|1|0|0| | Finally, it resets to its start position: | |1|1|0|0| |
About 100 years ago, Alonzo Church, a philosopher and mathematician at Princeton, saw the same pattern, and he developed a programming language based on sets. (This was before anyone had heard of programs and computers, by the way.) He called his language the lambda calculus.
Church made a set, (x | Px}, into a program by writing it like this:
Here is an example of a lambda-calculus program and running it:
Define Square = (λn (n * n)) Run it: Square(3) => (λn (n * n))(3) => 3 * 3 => 9The above example is ``sort of like'' 3 ∈ {n | n * n} but produces a number as an answer, not True/False. The above example is ``sort of like'' square(3) => 3 * 3 => 9, but the names, square and Square, aren't needed; we can just do this:
But lambda-calculus can do lots more than sets and ordinary algebra functions can: A program that runs with two arguments takes the arguments one at a time:
Define Mult = (λm (λn (m * n)))
Run it:
Mult(3)(4) => (λm (λn (m * n)))(3)(4)
=> (λn (3 * n)))(4)
=> (3 * 4) => 12
Lambda-calculus lets programs run with other programs as arguments,
like this:
DoTwice = (λp (λa (p(p(a)))))
DoTwice(Square)(3) => (λp (λa (p(p(a)))))(Square)(3)
=> (λa (Square(Square(a))))(3)
=> Square(Square(3))
=> Square( (λn (n * n))(3) )
=> Square(3 * 3) => Square(9)
=> (λn (n * n))(9) => 9 * 9 => 81
And self-inspection is as easy to state as the earlier examples:
Identity = (λx (x))
Identity(Identity) => (λx (x))(Identity)
=> Identity = (λx (x))
And we can code this version of Russell's Paradox:
Say that not is a program that behaves like this:
not(True) => False not(False) => True
Define Russell = (λS (not(S(S))))
Run it:
Russell(Russell) => (λS (not(S(S))))(Russell)
=> not(Russell(Russell))
=> not((λS (not(S(S))))(Russell))
=> not(not(Russell(Russell)))
=> not(not(λS (not(S(S))))(Russell))
=> not(not(not(Russell(Russell))))
...
Will the "paradox" ever be decided as True or False?
This is an example of divergence --- no answer.
It avoids the paradox by refusing to answer!
Divergence was not an option in mathematics, but it is an option in computing!
How is this coding different from the specification of Russell's Paradox seen earlier? (Hint: look at the definition of not.)
The previous example also shows the technique one uses to repeat an action over and over in the Lambda-calculus: if op must be repeated, then code (λS (op(S(S))))(λS (op(S(S)))). (There are some details missing; see the exercise at the end of this section.)
Church's Thesis is the claim that all computable activities can be written as lambda-calculus expressions. Later in time, many people proved that any program written in the language of the universal Turing machine can be written in lambda-calculus, and vice-versa. Hence, we have the Church-Turing thesis.
In 1958, John MacCarthy made the lambda-calculus into the computer language, LISP, which became the primary language for the writing of artificial-intelligence programs (an area that MacCarthy helped to invent).
Next, pretend that we have this operation, eqZero, such that eqZero(0) => True, and eqZero(n) => False when n > 0. (It is possible to code eqZero with a lambda-calculus expression, but we won't do it here.)
Use eqZero to implement this requirement as a lambda-calculus expression:
{ n |-> Square(n) iff n ≠ 0
|-> ↓1 iff n = 0 }