Chapter 5: Error-Correcting Codes

One way to verify correct transmission is to send the same data two or three times --- if the data are received identically, we are confident that the transmission is error free. (But what if the data was corrupted exactly the same way every time? There is never 100% confidence.)

If we send data twice, it is twice as large and takes twice as long to transmit. This is unacceptable for large files.

What happens in practice is that the data is sent with a small extra number, called its checksum, that somehow restates the data in an abbreviated, ``squeezed-in'' form. The transmitted checksum can be compared with the transmitted data to see if they agree. If yes, we have high confidence that the transmission was correct. If no, we have detected an error.

If we are really bold, we should find a version of checksum that would also tell us where to correct an error when it occurs. There is one useful (but limited) technique that does this. We look at this last. For now, we focus on error detection.

Intuition: Squeezing data

Hello there!  Hello there!

But say that the receiver gets this information:

Hellooo gere.  Hello there!

and the receiver computes this new checksum of the line: Hellooo gere. 
The checksum does not match the one sent, so the line should be resent.

Provide an algorithm that computes checksums: The algorithm's input is a data word (a long sequence of text or numbers or 1s and 0s), and the output is a (small) number, the checksum, which is unique to the data in the sense that if the contents of the data are changed, the value of the recomputed checksum changes, too.

Discussion

1. State some ways that we use to "squeeze" words in real-life: abbreviations, dropping vowels, etc. When/where do you use those techniques in real life? Why do you use them? How well do they work?
2. A simplistic way of squeezing a sequence of digits is to add the digits, e.g., 6 3 4 5 7 8 9 2 2 5 9 is squeezed to 6+3+4+5+7+8+9+2+2+5+9 = 60.

   Can we recover the original sequence from its squeezed number? Explain why not.

   Look at the above sequence of numbers. Then, close your eyes and state it, as accurately as you can, to your neighbor, who writes it down as best as (s)he can. Use the 60 to check if the neighbor wrote down the sequence correctly. Will this checking technique always work? If not, why not?

Word, blocks, ASCII

Remembr that text symbols are saved in computers via ASCII-numbers (e.g., space => 32; ! => 33; ...; 0 => 48; 1 => 49; 2 => 50; ...; A => 65; B => 66; C => 67; ...; a => 97; b => 98; c => 99; d => 100; e => 101; ..., etc. Look them up on the Web.)

For example, Hello there!, is the ASCII number sequence,

72 101 108 108 111 32 116 104 101 114 101 33

The text line is a ``word'', and each ASCII-number is a ``block.'' How do we squeeze all the blocks into just one, the checksum?

Baby exercise

Add the blocks

72 101 108 108 111 32 116 104 101 114 101 33 has the checksum, 72 + 101 + 108 + ... + 33 = 1101

This is easy, but if the word is corrupted by multiple errors during transmission or if any of its blocks are rearranged, or if some extra zeros are inserted (in ASCII, NUL => 0), the checksum might not reveal the error. Here are examples from MacCormick:

A word of five blocks and its checksum:

A single-digit-addition checksum can detect only one error at best. For this reason, one might compute multiple different checksums, each designed to detect different forms of errors in the transmitted text, and send the text with the multiple checksums. One might even use the checksum to detect where the error occurred and fix it. MacCormick presents the "pinpoint technique" (Pages 73-76) to do this:

Exercises

1. Study the diagram above of the pinpoint technique (from MacCormick, Pages 73-76). Modify the example by swapping two data numbers, and show that the pinpoint technique fails to identify where the errors are.

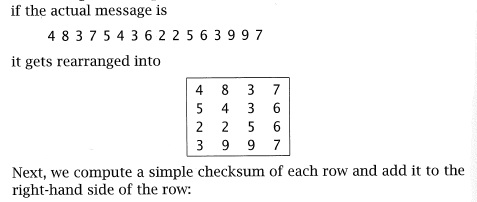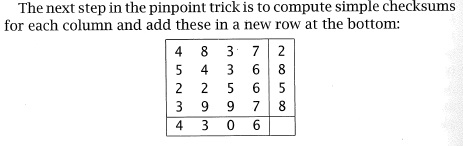   Next, start over, and alter one of the checksum numbers. How does this case look like the previous one? How is it different? Can you identify where the error is? Are there any patterns you can use to identify the source of an error when one or more checksums fail to add up?

2. MacCormick's examples are all stated in Base-10. But hardware uses data words that are stated in Base-2, that is, as long sequence of 1s and 0s. Instead of addition, we use exclusive or (XOR) to ``add'' the blocks of the data word. Here is the definition of XOR and an example where two four-bit blocks are XORed:

   0 XOR 0 = 0     0 XOR 1 = 1    1 XOR 0 = 1    1 XOR 1 = 0
   
   1 0 1 1  XOR  1 0 0 1  =   0 0 1 0
   
      we can write the operation like an addition:      1 0 1 1
                                                   XOR  1 0 0 1
                                                   ============
                                                        0 0 1 0
      and we need not worry about "carry bits" (-:
   

   For this data word, divide it into blocks of four bits, and compute a four-bit checksum by XORing ("adding") the blocks. (Hint: the answer should be 0 1 0 0):  0 1 0 0 1 0 1 1 1 0 1 0 0 1 0 1 0 1 0 0

How to truncate: modulo arithmetic

Some review: For integers a,b,  a mod b is the remainder left over after dividing a into b-equally sized parts. b is the divisor.

Example: 14 mod 3 is 2, because one can extract 3 parts of 4 from 14, leaving a leftover of 2. That is, 14/3 = 4 with remainder of 2; that is, 14 = (3 * 4) + 2; that is, 14 - 3 - 3 - 3 - 3 = 2. Pick the explanation that works for you.

For a mod b, the range of possible answers is 0,1,...(b-1).

The checksums computed in MacCormick add the blocks of a word, giving the total, and then compute the checksum as total mod 10.

• But the range of answers, 0..9, is too small. If we have a byte to hold the checksum, we should expand the range to as much as 0..255, which would indicate more errors.
• (Subtle but critical:) MacCormick's examples are stated in base-10 arithmetic (that is, expressed with digits 0,1,2,3,4,5,6,7,8,9). A divisor that is a multiple of 10 will never detect errors in the leftmost base-10 digits in the blocks!

  Example: the word, 22 33 44, has the checksum, 99 mod 10 = 9, as will 32 33 44, and 92 83 04, and so on --- the leftmost digits of the blocks are ignored because the base is 10 and the divisor is 10. If we change the divisor to 9 or 11, all three examples have different checksums.

Exercises

1. Modulo is computed by repeated subtraction, e.g., 14 mod 3 = 2 because 14 - 3 - 3 - 3 - 3 = 2. Compute these examples, doing so by repeated subtraction: 16 mod 3; 8 mod 5; 18 mod 6; 2 mod 4.

   Modulo is computed as the remainder left over from a long division, e.g., 12,449 / 11 = 1131 with a remainder of 8. Compute these examples, doing so by long division: 12,449 / 6; 12,449 / 22.

2. We saw that 10 was a poor divisor for base-10 numbers. But so is 5: calculate the checksum for these examples by adding the blocks and doing mod 5: 20 15 31; 40 15 21; 400 25 3001. Which digits are "ignored" by the checksums?

   The point is, when working in Base-B arithmetic, the divisor for modulo and B should not have a common divisor (except for 1). (Here, both 10 and 5 have the common divisor, 5.) That is, the base and the divisor should be co-primes.

Fletcher's checksum: Add twice then modulo

Fletcher's checksum algorithm

INPUT: a data word (e.g., a sequence of ASCII-numbers)
OUTPUT:  two checksums for the word, each sized to fit in one byte
ALGORITHM:
1.  divide the  Word  into a sequence of equally-sized blocks,  b1 b2 ... bn
2. define two checksums, starting at  C1 = 0  and  C2 = 0
3. for each block, bi,
        add  bi to  C1
        add the new value of  C1  to  C2
4.  compute  Checksum1 = C1 mod 255   and  Checksum2 = C2 mod 255
5.  return  Checksum1  and  Checksum2

Word  is  72 101 108 108 111 32 116 104 101 114 101 33    ("Hello There!" in ASCII)
Each ASCII-number is a block.

For each block, the values of  C1   C2  become:
--------------- ---------------------------------
                                0     0
72                             72    72
101                           173   245   
108                           281   526
108                           389   915  
111                           500  1415
...                           ...   ...
33                           1101  7336

Checksum1 = 1101 mod 255 = 81
Checksum2 = 7336 mod 255 = 96

Exercise

Optional material: Cyclic Redundancy Check

A packet is a sequence of 0,1s; treat the packet as one single block. The checksum is merely the modulo operation but this time computed by polymonial division on Base-2. (In algebra class, you learned polynomial division on Base-10.) Polynomial division on Base-2 turns out to be repeated use of the exclusive-or operation (XOR) on the block and the divisor, starting at the left of the block and shifting rightwards one bit after each XOR.

This technique is called a Cyclic Redundancy Check (CRC). It is fast and is the most commonly used checksum technique. Here is a worked example, where the data is 010100001001 and the divisor for the modulo calculation is 1011. This will produce a 3-bit checksum. Match the long division to the XOR operations:

The choice of divisor is critical, and there are different values chosen for detecting certain forms of transmission errors. Here is a table of some commonly used ones (but don't ask me why!):

   (from Ramabadran and Gaitonde, ``A Tutorial on CRC Computation", IEEE Micro, 1988)
   

CRC is a bit complex, so here are a couple of references for you:

http://kilyos.ee.bilkent.edu.tr/~ee538/crc.pdf

https://en.wikipedia.org/wiki/Cyclic_redundancy_check

Hash numbers

Choose a "hash base", b (e.g., b= 2 or b= 10 or b= 37)

For a word of integers of length n+1:
    w =  x0 x1 x2 ... xn-1 xn,

Compute this hash number:
    hash(w) =  (x0 * bn) + (x1 * bn-1) + (x2 * bn-2) + ... (xn-1 * b1) + xn

1) for  word = 4 5 6,
      when  b = 10,
           hash(word) = (4 * 102) + (5 * 101) + 6  =  400 + 50 + 6  =  456
      when b = 100,
           hash(word) = (4 * 1002) + (5 * 1001) + 6  =  40000 + 500 + 6  =  40506
      when b = 5,
           hash(word) = (4 * 52) + (5 * 51) + 6  =  100 + 20 + 6  =  126
      when b = 2,
           hash(word) = 16 + 10 + 6 =  32
      when b = 1,
           hash(word) = 4 + 5 + 6 = 15

2) for word = 12 33 08,
      when b = 10,
           hash(word) = (12 * 102) + (33 * 101) + 8  =  1200 + 330 + 8  =  1538
      when b = 100,
           hash(word) = (12 * 1002) + (33 * 1001) + 8  =  120000 + 3300 + 8  =  123308
      when b = 5,
           hash(word) = (12 * 52) + (33 * 51) + 8  =  300 + 165 + 8  =  473
      when b = 2,
           hash(word) = 48 + 66 + 8 =  122

Example 2) shows clearly how blocks can overlap a little bit (when the base is 10, notice how 33 overlaps part of 12 and part of 08), not at all (when the base is 100), or a lot (the base is 5 or 2), when hash numbers are computed.

The hash formula is great, because you can "tune it" to the amount of "squeezing" you want to do. There is a deep theory to hash-number calculation, and in particular, when a base is used that causes the values of the data blocks to overlap/"squeeze", it is important that the base be a prime number, because this retains, as much as possible, the uniqueness of the hash number for each data word. 37 is commonly used as a base for hash-number calculation.

If the words that we must hash have varying lengths, the hash numbers we compute might get too huge. If we wish to limit the range of the hash numbers to, say, 0..(p-1), we can use a modulo operation:

hashCode(word) = hash(word) mod p

Discussion

Exercises

1. For hash base, b = 2, compute the hash numbers for these data words: 2 3 4;   1 5 0. Now, find, as many as possible three-digit words that have the same hash number as these two.

   Change the hash base to b = 3, and find some three-digit words that have the same hash number as 2 3 4. Repeat this experiment for b = 9 and 2 3 4 --- any luck? Why not? (How about b = 9 and 0 1 0?)

   Explain why it is impossible for every three-digit data word to have a unique, distinct hash number for any base b < 10. (Hint: what is the hash number for 9 9 9 for hash base b < 10? Is it more or less than 999?)

2. Remember that a data word's hash number is meant to "squeeze" the number into a smaller space. Since large data words generate large hash numbers, we must choose a modulo divisor to limit the range of the numbers. Here's why the divisor and the hash base should be co-primes:

   Consider again three-digit words and hash base b = 10. This means the word 2 3 4 has hash number 234. It also means that every three-digit word has a unique hash number. This seems great, until we learn that the hash codes must fall in the range 0..9, that is, the modulo divisor is also 10. Explain why: (i) of the 1000 possible hash numbers, exactly 100 of them map to the same hash code. (This seems to be as good as one would hope.) (ii) but, there is a serious "structural flaw" about how those 100 hash numbers are chosen to all map to the same hash code.

3. The "structural flaw" mentioned in the previous exercise is a killer when the data words are actually text words. Here's why: Say that we use this numbering for part of the alphabet:

   a => 0; b => 1; c => 2; d => 3; e => 4;

   f => 5; g => 6; h => 7; i => 8; t => 9

   So, the word, bed, becomes the three-digit data word, 1 4 3; the word, feed becomes 5 4 4 3, and so on.

   Now we want to translate a sentence of words into a sequence of hash codes. For hash base b = 10, translate this 7-word sentence into a sequence of seven hash numbers:

   big cat had bad feed cat dead

   (You get 186 209 ... 3403, yes? It's meant to be easy.)

   Now, say that the hash codes cannot be larger than 15 (perhaps because they must be stored in four bits in the computer). Calculate the seven hash codes for the words in the previous sentence, when the modulo divisor is 10; when the divisor is 15; when the divisor is 13.

   Which results look poor and why?

   The point is, in English, certain letters show up often and in the same position in commonly used words, so a hash code must represent all the letters of each word for an "accurate squeezing" of distinct words into distinct codes. This is why the hash base and the modulo divisor should be coprimes.

4. (This exercise requires a bit of programming knowledge.) The previous exercise leads us to the most important use of hash codes in computing: using them as indexes into an array. An array of length n can accept indexes that are only integers, only in the range of 0..(n-1).

   Say we have an array, table, of length 997, and we would really prefer to index it with text words, and not integers, (e.g., sort of like table["cat"])! (Maybe table will hold a "dictionary" of "definitions" of text words.) How can we make this happen (almost)? Is there any potential problem awaiting the (obvious) approach?

   There is a rich theory of hash tables and dictionaries that builds on this approach.

Optional material: Hamming Codes

A parity bit is a simple 1-or-0 checksum for a binary data word: the parity bit has value 1 if there are an odd quantity of 1-bits in the word and 0 otherwise. For example, the parity bit for 0 1 1 0 0 1 1 is 0, since there are four 1s. When a data word and its parity bit are transmitted, the parity bit is used as a primitive, imperfect checksum.

Hamming's insight was that if a word could have multiple parity bits, where each parity bit counts the 1s in different, but overlapping, parts of the data word, the checksum would be more effective, and in the case of an error, even indicate the exact position of the error. (An indeed, since the only possible values are 0 and 1, an error is repaired by flipping the bit! But this technique works for identifying at most one error in a word.)

Say that we have a word that is four bits of data. The Hamming(7,4)-coding would add three parity bits to the four bits. The parity bits are mixed with the data; here is the layout:

BIT#:    1      2       3   4      5  6  7
        -------------------------------------------
PURPOSE: P3,5,7  P3,6,7   D  P5,6,7  D  D  D

    where  D  is a data bit, and  
    Pa,b,c,...  is the parity bit for data bits at  a,b,c,...

Examples:
DATA 3 5 6 7  PARITY FOR 3,5,7  PARITY 3,6,7  PARITY 5,6,7    HAMMING CODING
---------------------------------------------------------------------------------
     0 1 0 0             1             0             1        1 0 0 1 1 0 0
     
     1 0 1 1             0             1             0        0 1 1 0 0 1 1
     

The pattern shown above is meant to be extended to longer-sized blocks with more parity bits mixed in. The reason for mixing the parity bits with data is that a matrix multiplication can be used to analyze a received word-plus-parities to calculate where there is an error (and repair it), if any.

MacCormick gives some examples of Hamming codes on Page 67:

Here is a decent explanation of Hamming codes:

https://en.wikipedia.org/wiki/Hamming_code