Chapter 4: Public-key cryptography

MacCormick explains a clever technique that helps two strangers send secret (encoded) messages on the internet.

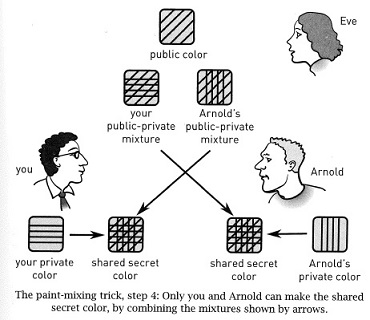
Information sent on the internet is like sending a post card in the U.S. Post --- the postal carriers can read the post card on its way to delivery. For this reason, we need a way of encoding the information written on the ``post card'' so that the ``postal carriers'' cannot read it.

The information on the post card will be encoded using a secret number that is known to only the author of the card (the sender) and the card's receiver.

One way to encode a message is first to rewrite it in its ASCII numbers, a standard computer coding, e.g., A => 65; B => 66; C => 67; etc., and then add the secret number to each numbered letter. E.g., "a cab" is converted to 65 32 67 65 66, where 32 is the ASCII number for a space. If the secret code number is 21, then the encoded message is 86 53 88 86 87.

The previous coding is ``weak'' --- it can be guessed by a smart human. A stronger technique makes the entire message (or each line of the message) into one long number and adds a (very large) secret number to it, e.g., the line "a cab" is converted to the single number, 6532676566, and the secret number, say, 253445763, is added to it, making the encoded message, 6786122329. To decode, just subtract the secret number and convert the ASCII numbers back to letters. (As MacCormick mentions, the coding can be further strengthened by rearranging/inverting the lines, etc.)

The sender of the post card and the receiver must both know the secret number but no one else knows it. But what if the sender and receiver are strangers to each other? How will they both know the same secret number?

The requirement for an encryption program

Provide an algorithm for communication (called a protocol) that a person can use to send a computerized, encrypted message to a stranger so that the stranger can decrypt the message but no one else can.
This sounds like an impossible requirement, but the public-key encryption technique will satisfy it! But to do so,
  1. although they are strangers, both the sender and receiver must know how to use the public-key-encryption protocol.
  2. not one, but four "post cards" (messages) must be mailed, where the last message contains the encrypted message
The "mail delivery people" will be unable to decode and read the encrypted message when it is finally mailed on the 4th post card.

Needed: a mathematical operation that has no inverse

The public-key-encryption protocol requires a binary (two-argument) math operation that cannot be undone. Call it the ''locking operation.''

Example: Addition is a binary operation. 3 + 2 computes 5. But addition can be undone with subtraction: if we know 5 and that 2 is one of the arguments, we can discover the other argument with addition's inverse operation, subtraction: 5 - 2 equals 3. More precisely, 

if  
  x + y = z,
then knowing the values of  z  and  x,  we can solve for  y  as
  y = z - x
So addition cannot be used as the locking operation. Neither can subtraction (why?), multiplication, division, etc.!

For reasons explained a bit later, the unlockable binary math operation requires a commutativity property.

Here's the bad news: no one knows a binary math operation with the commutativity property that cannot be undone. But the good news is, there is a complicated math operation that is a combination of exponentiation and remainders-of-large-prime numbers that no existing computer can undo in years and years. (To make the last phrase more precise, we have to study computational complexity theory, which we may well do by the end of this course!) The exponentiation-remainder operation will work well enough as the locking operation.

We call the exponentiation-remainder operation lockOp. We'll use it like this: starting from a ``public number'' p, we lock up a private number, num, like this:

p lockOp num
The number that is the answer has num locked inside it, and even if we know p and the definition of lockOp, we cannot undo the answer/calculate the inverse to extract num. MacCormick explains lockOp on Pages 51-56. The commutativity requirement is stated: for numbers, x,y,z, 
(x lockOp y) lockOp z equals (x lockOp z) lockOp y)
that is, we can lock up y and z together, and the order in which they are locked does not matter.

Discussion question

A lockOp operation is a great technique for hiding secret numbers/passwords, etc., on the computer. But once you lock up a number, you can never recover it again! Still, think of at least one or two uses of lockOp besides the one explained in this Chapter.

The protocol for public-key encryption

On Page 51, MacCormick shows how the protocol works when lockOp is a color-mixing operation:
On Page 57, MacCormick pretends that all humans have forgotten how to do long division by hand (a not-so-far-fetched scenario, alas!), meaning that multiplication can be used as lockOp:
Here is the protocol written out, so that person Sender sends an encrypted message to a stranger, person Receiver. IMPORTANT: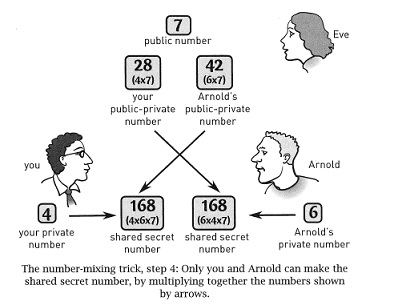 The protocol requires that four messages (``post cards'') are mailed:
  1. Sender thinks up a brand new number, p, called the public number.

    Sender writes the first ``post card'' to Receiver that says, ``Hello, Receiver! I want to use public-key encryption to send you a secret message. Please start with this public number, p.'' The post card is mailed.

  2. Receiver gets the post card, reads it, and computes RPP = p lockOp r. (MacCormick calls this ``Receiver's private-public number.'')

    Receiver writes the second post card: ``Hello, Sender! I got the public number! Here is my number for you: RPP.'' The post card is mailed.

  3. Sender gets the post card, reads it, and remembers the number, RPP. Now, Sender computes SPP = p lockOp s, and writes the third post card:

    ``Hello, Receiver! I got your number! Here is my number for you: SPP.'' The post card is mailed.

  4. At this point, Sender knows s and RPP. Sender computes the secret key (the ``shared secret number'') as RPP lockOp s. (This equals (p lockOp r lockOp s).)

    At this point, Receiver knows r and SPP. Receiver computes the secret key as SPP lockOp r. (This equals (p lockOp s lockOp r) which equals (p lockOp r lockOp s).)

  5. Finally, Sender writes the encrypted message: The message's text is converted to ASCII numbering, the secret key is added to the ASCII numbering, and the resulting number, call it codedMess, is written on the fourth post card and mailed to Receiver.

    When Receiver gets the fourth post card, it decrypts codeMess by subtracting the secret key from it and converting from ASCII back to letters.

During these steps, what does a nosy postal worker (internet-router ``sniffer'') know? Because RPP and SPP were computed with lockOp, it is impossible for the sniffer to ``unlock'' them and calculate either s or r. So, the sniffer cannot compute the secret key and cannot decrypt codeMess, even if the sniffer knows how the protocol goes and even knows what the lockOp is!

Please double-check the above protocol by reviewing the diagram from MacCormick, Page 57.

Exercises

  1. Find three people in the room, all of whom remember how to do multiplication with pencil and paper but have forgotten how to do long division. These three people perform a use-case of the protocol, where lockOp is multiplication. Do it.

    Next, find a fourth person who remembers how to do both multiplication and long division by hand. Let that person sit with the three people and monitor the communication. Do it again. What happens?

Discussion question

No known protocol is perfect, but the ones in use are pretty good. Consider this scenario: the Sender mails the first post card to the Receiver. A dishonest PostalWorker keeps the card and writes a fake postcard to the Receiver, claiming to be the Sender. When the Receiver replies, the PostalWorker intercepts and keeps the card and writes a fake reply postcard to the Sender. And so it goes.

The PostalWorker has inserted itself in the middle of the communication --- the Sender is now communicating with the PostalWorker and the PostalWorker is now communicating with the Receiver. There are two communications going on; the PostalWorker is a participant in both; the Sender and Receiver are clueless. This is known as the ''man in the middle'' attack.

Discuss how the U.S. Postal Service can prevent this attack. How might this strategy be adapted to computer routers?

Optional material: Diffie-Hellman's lockOp

The locking operation used in Chapter 4 was devised by Diffie and Hellman. Here is an explanation. The operation uses exponentiation (repeated multiplication) and modulo (remainder --- repeated subtraction): Now, exponentiation can be easily undone, by repeated division. For example, given answer 16 and base, 2, we can solve for the missing exponent: 16/2 = 8; 8/2 = 4; 4/2 = 2; 2/2 = 1; stop. We did 4 divisions. We say that 4 is the base-2-logarithm of 16. Formally stated, when n = basepow, then pow = logbasen.

In contrast, modulo does not have an inverse operation. For example, if 2 is the answer for n mod 3, the best we can say is that n is one of 2,5,8,11,....

Recall this technical requirement of lockOp, a form of commutativity: For integer arguments x,y,z: 

(x lockOp y) lockOp z  =  (x lockOp z) lockOp y
This requirement is needed so that the Sender and Receiver can compute the same shared secret key.

Hellman and Diffie build lockOp to meet the requirement. Let Clock be a preselected number that defines the range of remainder answers. (E.g., if Clock is 3, then the possible answers are 0, 1, 2.) For technical reasons, Clock should be a prime number. (The definition of prime is at the end of this page.) 

Define   x lockOp y =  (xy) mod Clock
Once you study some group theory, you will be able to prove that lockOp satisfies the commutativity requirement. Further, there is no way to undo (easily!) lockOp:

Say that we already know integers x and SPP, and SPP has locked inside it an unknown integer, y, which we want to know. That is, SPP = x lockOP y. Since SPP = (xy) mod Clock, we deduce that

xy = (d * Clock) + SPP
for yet another unknown integer, d.

Solving for both y and d is tough. One must grind out all possible values for d = 0,1,2,... and for y = 0,1,2,... and keep checking the repeated multiplications and subtractions until an answer is found. As MacCormick notes, real-life von-Neumann-based computer architectures, regardless of processor speed or parallellism, cannot finish this for years and years, assuming that the value of Clock is a prime number that is several hundred digits long (that is, over one-thousand bits in length).

(Some bad news: Hellman-Diffie's lockOp operation has the flaw that we only need to try the finite range of values y = 0,1,2,...,(Clock-1) when trying to unlock. The flaw arose because lockOp needs the commutativity property! A good exercise is to study the table on Page 54 and use it to convince yourself of this point.)

There are other locking operations besides this one, but MacCormick chose this one because it is famous and easy to explain.


FOOTNOTE: Integer, p, is called prime if its only divisors are itself and 1 --- stated precisely,
an integer p > 1 is prime exactly when the only answers for p mod d = 0 are d = p and d = 1.
Here are some primes: 2,3,5,7,11,13,17,19,23,29,.... Integer 4 is not prime because its divisors are 1,2,4. (Verify that the integers missing from the previous list, in the range of 2..30, are not primes.)

An easy-to-prove but profound result of number theory is that there are an infinite quantity of primes.

Primes work well for the value of Clock in the definition of lockOp because they force the repeated subtraction that tries to ``unlock'' a number to repeat the maximum times possible, making unlocking almost impossibly hard.

Primes reappear in the next chapter.