
The Google search engine tries to meet this requirement. The program does not monitor all the traffic on the Web to satisfy the requirement! Instead, it is based on these principles:
A path in a graph is a list of the names of the arcs/arrows that one follows from a node to another node. A path can contain the same arc more than once, and a path can have infinite length (although infinite-length paths aren't so useful).
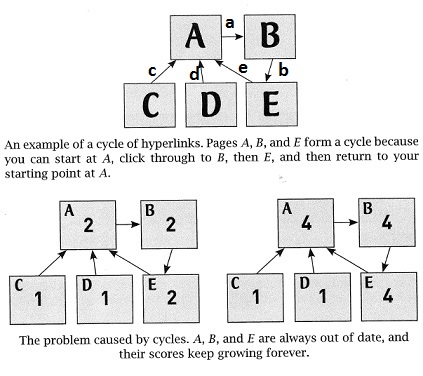
Graphs have no starting (entry) point, and a graph can have cycles (a sequence of arcs that begins and ends at the same node).
This suggests that a Web page, A, is visited more often (and is "more important") than another page, B, if more paths in the graph lead to A than to B.
Actually, Google does maintain a massive graph that contains most all the pages on the Web. How might Google maintain the graph, that is, keep it up to date?
Google's search engine does not (and cannot) generate all the finite paths through the Web's graph in any ``reasonable'' time.
MacCormick burns a lot of pages in Chapter 3 trying to compute importance rankings in terms of an "authority count", but he discards all this material because it doesn't work due to cycles.
This leads us to Google's "random surfer" technique, which
We have no way of proving, with mathematics, that the random-surfer technique computes the definition of "importance". We have merely a technique, a ``hack,'' that works well in practice!
They show how a cycle wrecks the "authority count" technique and how we might use (random surfing of) paths through the graph to measure importance.

For the above graph, whose nodes are A,B,C,D,E and whose arcs are a,b,c,d,e as marked, here is a sample path:D d A a B b E, which we write as just d a b. This path has length 3. A path can mention the same arc more than once, e.g., d a b e a b. (We won't worry about paths of length 0!)
Next, count how many times each of nodes A,B,C,D,E appear in all the paths. Which node is "most important" (appears most often)? Calculate the percentages: total all the occurrences of all the nodes, and then for each of A through E, compute its percentage, e.g., occurrencesOfNode_A / allOccurrencesOfAllNodes. Compare the percentages to those shown in the diagram on Page 35.
Now be patient and calculate all paths of length 10 or less and then the totals and then the percents. How do these match to those on Page 35? As we add more and more paths of longer length, how will the percentages change?
These experiments suggest that the random-surfer algorithm has been adjusted to reduce the influence of cycles.
Recall that a set is a collection of elements, each of which appears exactly once, and the order of elements does not matter. For example, {penny, dime, quarter} is a set, but {penny, penny} is not a set. {dime, penny, quarter} is the same set as {penny, dime, quarter}.
For a path in a graph, its arc set is the set of arc names that appear in the path and its node set is the set of node names that appear in the path. For example, for path d a b e a b, its arc set is {a,b,d,e} and its node set is {A,B,D,E}.
Important: given a path's arc set, we can calculate the path's node set directly from the arc set. Explain how to do this and why the answer will be correct.
Here is an algorithm to calculate the "importance" of nodes in a graph:
INPUT: a graph of the Web OUTPUT: for each node in the graph, the percentage of how often the node is visited ALGORITHM:
- Generate all the arc sets of all the paths in the graph.
- For each arc set, generate its node set.
- For each node in the graph, total all the occurrences of the node in all the node sets.
- For each node, calculate its percentage, as described earlier.
Here is an example of the algorithm in action. For this graph:
Nodes are A,B,C; arcs are a, b1, b2:
+---> C
a / b1
A ---> B
\ b2
+---> D
We calculate these paths, arc sets, node sets, and totals:
PATH ARC SET NODE SET
---------------------------------
a {a} {A,B}
a b1 {a, b1} {A,B,C}
a b2 {a, b2} {A,B,D}
b1 {b1} {B,C}
b2 {b2} {B,D}
Total occurrences: A B C D
----------------------------------------
3 5 2 2 = 12
Percentage: 25% 41% 17% 17%
Node B is "most important" in this graph.
Notice that {b1, b2} and {a, b1, b2} are not arc sets --- why not?
Important: we can generate all the arc sets in a graph without generating all the paths first. Explain how to do so and why the answer will be correct, even if there are cycles.
Explain how this algorithm approximates the number of times a node is visited via all possible paths through a graph. This algorithm is an example of a "mathematical technique" for computing importance rankings.
ARC SET NODE SET
-------- ---------
{a} {A,B}
{a,b} {A,B,E}
{a,b,e} {A,B,E} (A does not appear twice in a set!)
{b} ...
{b,e}
{c}
{c,a}
... ...
{d}
... ...
{e}
...
How do the percentages you calculate compare to those done by the random surfer on Page 35?
Explain how the importance of cycles are deemphasized by this algorithm.
Explain why, even when there are an infinite number of paths through a graph --- like the one you just worked --- there are only finitely many distinct arc sets. (This is critical to making the algorithm finish its work in finite time!)