This is the online version of technical report KSU CIS TR-98-12. It includes hyper-links to numerous relevant resources and complete details of the example described in the report. The postscript version of the paper is here.
This document is a tutorial introduction to a toolset for translating Ada source code to the input format of the SPIN model checker [Hol97] (i.e., Promela code) and the SMV model checker [McM93].
This toolset provides completely automated translation for most steps in the process of generating a safely approximating state transition model of a software system's run-time behavior. This process, as supported by the toolset, is illustrated in Figure 1.
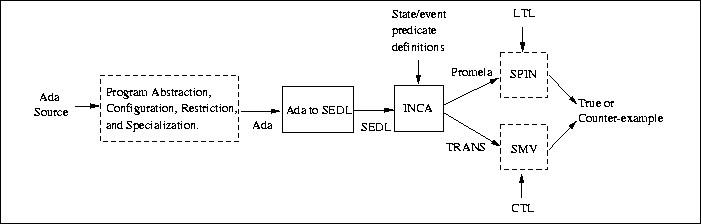
Figure 1: Ada Translation Toolset
There are seven steps in model checking properties of an Ada program.
98b] for techniques which can convert general Ada programs
to a finite-state variant.
The Ada programs that can be fed to step 2 can be thought of as static finite-state Ada programs. The Quechua [Cor93] language defines the data types and operations that such an Ada program may contain (although Quechua's syntax differs slightly from legal Ada). Finite-state Ada programs have a fixed number of tasks, they contain no pointer-based referencing of tasks, and their data is defined over a discrete finite type (e.g., sub-ranges, enumerations, booleans). We refer the reader to Quechua for details of legal input Ada programs.
It is well-understood that cost-effective model checking of complex
systems requires abstraction [CGL94, Dam96, LGS 95].
One crucial issue in translating source code to
a highly-abstracted finite-state transition system for
model checking is insuring
the correspondence between the features of the source code
that are to be reasoned about and
features of the transition system to be checked.
For example, one may be interested in reasoning about sequences
of calls to procedures in a program (e.g., that calls to open
are always followed by calls to close).
Translations must reveal the states of
the transition system that correspond to the program
features of interest (e.g., open calls).
Furthermore, a mechanism that allows
these features to be referred to in property specifications
that are to be checked must be provided.
The toolset described here defines just such a mechanism;
it is referred to as predicate definition, even though it
provides a means for defining the set of proposition to be used
in temporal logic specifications.
This predicate definition facility is used in step 3 by the
tool user and in step 4 by the translation toolset.
One nice feature of the predicate definition facility is that
it is independent of the particular
model checker to be used. The same predicate definitions can
be used to define the propositions for checking a CTL [CES86]
specification with SMV or an LTL [MP91] specification with SPIN
in step 5.
Once the model checker has completed execution, in step 6, its results need to be interpreted, step 7. A false result will be accompanied by a counter-example, i.e., a path through the transition system that violates the specified property. Model checkers express counter-examples in terms of sequences of transition system states. This is problematic for programmers who are familiar with the code, but not the details of the translations produced by the toolset. By incorporating predicate definitions in step 4, the tools allow counter-examples to be expressed in terms of source program features that the user is interested in, thereby greatly simplifying the interpretation of counter-examples.
This tutorial is example driven; the complete details of this example, including source code, specifications and intermediate files, have been collected on the web-site http://www.cis.ksu.edu/~dwyer/ada2model. We begin with an overview of how a simple property of a program is checked. In the next section, we define the underlying model of concurrent programs that the translation tools are based on. We then proceed with a detailed discussion of steps 2-7. We conclude with a description of features that might be included in future generations of similar translation toolsets and a summary.
This overview is intended to be high-level, but we do provide links to all of the details of the example. On first reading it may be best to skip those details until the reader has read the later sections of the tutorial.
Consider the classic readers writers
problem (as described in e.g., [ABC 91, Cor96, Cha96])
and a simple invariance property stating that: writers
cannot work while some reader is active.
We might specify this in LTL as [](callwriteWork -> activereaders0),
where
callwriteWork indicates that a writer's procedure writeWork is called and
activereaders0 indicates that the variable ActiveReaders
in the Read_Write_Control task has a value of zero.
The finite-state Ada code for the 2 reader-1 writer program is given in a file rw21.a. Executing the command
$ ada_to_sedl rw21produces the file rw21.sedl.
We define predicates for the propositions that appear in our specification by putting the defpredicate forms in Figure 2
Figure 2: Predicates for Readers-Writers Invariance Property
in a file named rw21.query.
Invoking the rest of the translation tools requires starting the LISP environment. Once LISP is running the INCA toolset is loaded, then the derive and spin-input commands are executed.
$ lispworks
...
USER 4 > (load "inca.lisp")
USER 5 > (derive "rw21" :expose '("writeWork"))
USER 6 > (spin-input :embed '("callwriteWork") :define '("activereaders0"))
USER 7 > (bye)
These commands produce a SPIN input file rw21.prom.
The LTL specification [](callwriteWork -> activereaders0) is submitted
to SPIN to render it as a never claim that can be included
into rw21.prom.
Executing SPIN requires several commands.
$ spin -a rw21.prom $ gcc -o pan pan.c $ pan -aThe results of executing pan indicate a successful model check (i.e., the property is true of the program) so there is no counter-example to interpret and hence no step 7.
Versions of the readers writers problem are readily available as static finite-state Ada programs. We have selected a version with two reader tasks and one writer tasks. We have added procedure readerWork and writerWork which are called from the reader and writer tasks, respectively. The source code for this system is file rw21.a.
We check the following collection of correctness properties for this system. For each property, we describe it in English, as a specification pattern [DAC98b, DAC98a], as LTL and as CTL.
[](callwriteWork -> activereaders0) in LTL andAG(callwriteWork -> activereaders0) in CTL.[](callstartwrite -> <> callstopwrite) in LTL andAG(callstartwrite -> AF callstopwrite) in CTL.[](callstartwrite -> <> (callstartread1 || callstartread2)) in LTL andAG(callstartwrite -> AF(callstartread1 | callstartread2)) in CTL.
These specifications are written using a set of six propositions describing different aspects of executable system behavior in terms of features of the source code:
Predicates and their encoding into model checker input
are defined in terms of INCA's internal model of
concurrent programs as a set of communicating finite-state
automata (CFSA)
. We define this model to clarify the
subsequent definition of predicates.
A CFSA is denoted 
where:
is a set of local states
is a set of actions
is a transition relation
is the start state
are the final states
.
The local states typically represent points of control within
a task and may also encode the values of finite-ranged variables
that are critical for modeling the program behavior related
to the property being checked.
The concurrent system modeled by a set of n automata,
, can be
defined as another automaton 
where:
are global states
iff 
:
is the global start state
are the global final states
is in the alphabet
of either one or two of the .
Symbols in the alphabet of a single are called internal
actions and represent the execution of code within the corresponding
task; symbols in the alphabets of two are called communication
actions and represent a rendezvous between the corresponding
tasks.
Ada allows accept statements to have bodies where the accepting tasks
can execute while the calling task is blocked. This is modeled by
a pair of rendezvous one for the start and one for the end of the
accept body.
Ada is converted to SEDL using the IRIS-Ada toolset [FSZ88].
This consists of typical compiler front-end processing, the generation
of control-flow graphs for tasks and procedures in the program,
and finally emitting of SEDL.
The shell script ada_to_sedl acts as a driver for this sequence
of tools .
The script accepts a list of basenames for Ada files with the .a
suffix.
For the readers-writers example the command:
$ ada_to_sedl rw21produces the file rw21.sedl.
Known bugs in the implementation of cfgs_to_sedl include:
In this presentation, we interleave the description of the syntax and semantics of predicate definitions. Predicates define collections of local states in a CFSA model of a program that share some common feature. Features can include, calls to or returns from specific procedures in the program, the occurrence of a rendezvous communication between tasks in a program, the occurrence of a named internal action in the CFSAs, or program variables attaining specified values.
All predicates have a name. These are the proposition names that will be used in LTL/CTL specifications submitted to the model checker. Naming conventions in model checker input languages require that the predicate names begin with a lower-case alphabetic character.
Sometimes we are interested in reasoning about the sequencing of program events rather than the sequencing of program states. The distinction may seem subtle at first, but it can have a significant impact on the specification one writes. While it is true that events trigger state transitions, if one is interested in reasoning about a state (e.g. x>3) it can be very awkward to specify that state using events (e.g., one would have to interpret the events that modified variable x). On the other hand, if one is interested in reasoning about a sequence of events (e.g., the number of times an elevator arrives at a floor) it can be awkward to specify this in terms of transitions in state values (e.g., counting transitions from atfloor being true to being false and vice versa). For these reasons, both event and state predicates are supported.
A limited set of program events can be represented in predicate definitions: user-defined events that have been added to the system and rendezvous communication. Note that procedure call and return events are currently supported through a different mechanism (see :expose below).
An event predicate is true if and only if any task containing the event specified is in a state immediately following a transition on that event.
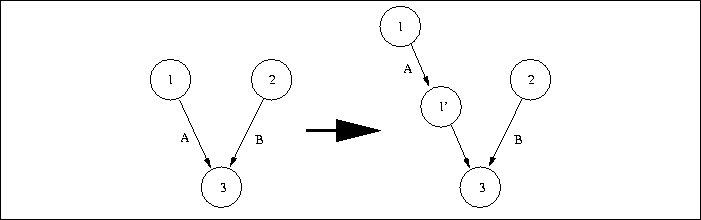
Figure 3: Internal Events and FSAs
For example, state 3 in the CFSA on the left side of Figure 3 immediately follows a transition on A or B. Note that this does not necessarily mean that the event just occurred--other tasks may have made transitions since the event (i.e., another CFSA made a transition). In fact, if there are multiple transitions into the state, the event may not have occurred at all since the state may have been entered on a transition not labeled with the event (e.g., even though state 3 is after a transition on A it could be entered by a transition on B). If you wish to uniquely define the occurrence of an event you should embed rather than define the predicate (see :embed below).
Events are defined by a string (note that white-space in the strings is not allowed even though the grammar allows for them). Strings which consist of only an identifier specify a user-defined events. Such an event, and its associated post-state, are inserted into the CFSA using the internal directive in SEDL. The right-side of Figure 3 illustrates the CFSA structure introduced for an (internal "A") directive in a branch of a conditional that has a B action in its other branch. An event predicate will match any occurrence of a user-defined event with the indicated name (e.g., (after "A") is true if any task is in a state following an (internal "A") action). Note that the CFSA generated for a system containing an internal action will contain only one transition (e.g., labeled with "A") into the states where the corresponding after event predicate (e.g., (after "A")) is true. In this case, the after predicate does guarantee the occurrence of its event since no other event leads to that state (e.g., in the figure event B does not lead to state 1')
Strings which begin with the call prefix correspond to pre-defined events which are generated to model rendezvous.
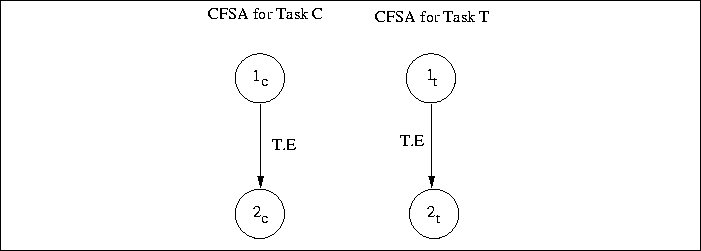
Figure 4: Communication Events and FSAs
Such an event corresponds to simultaneous transitions in two CFSA on a
shared symbol. Figure 4 illustrates such
a situation.
A predicate definition that matches such an event is encoded as
a string using the names of the participating tasks and the name
of the entry (e.g., (after "call(C;T.E)") is true in states
in which task C has just completed a rendezvous with task T at entry E).
Entry calls can have parameters that can
be encoded into the call string as a semi-colon separated list;
only literal values can be supplied and values for all parameters
must be given in the order of the parameters of the call.
Output parameters of entry calls with accept bodies are modeled
as parameters to explicitly defined call-back rendezvous
(details of this await implementation of this capability in ada_to_sedl).
The event predicates for the rw21 example are given at the top of Figure 5.
Figure 5: Predicates for Readers-Writers Properties
A state predicate specifies a task and a boolean expression over the values of that task's variables. As discussed below, one can model each task as a CFSA which interacts with those of the other system tasks. The state predicate is true in states of that task's CFSA where the expression would evaluate to true.
The expression must be legal Quechua [Cor93]. The tools perform only minimal type checking, so care should be taken. An expression can be tested for legality by placing it in an (assume <expr>) statement in the SEDL task specification; the INCA deriver (discussed below) will then perform all necessary checks to insure legality.
Only variables local to a single task may be used in an expression. This localization of predicates is not a significant limitation for specifying properties of systems. For example, if one wishes to describe the system state where variable x in task A is positive and variable y in task B is equal to zero, one defines two predicates:
(defpredicate "xpos" (in-task A (> x 0))) (defpredicate "yzero" (in-task B (= y 0)))then uses the conjunction xpos && yzero in the temporal logic specification. Because predicate definitions are local, due to the nature of the CFSA model, relational predicates (e.g. x=y) cannot be expressed for variables in different tasks.
To check parameter values, use event predicates--the parameter values are encoded in the string for the rendezvous as described above. There is currently no support for checking parameter values of procedure calls or global variables.
State predicates for the rw21 example include at the bottom of Figure 5.
The INCA toolset consists of a component called the deriver.
This component converts a program expressed in SEDL into
a collection of CFSA, one for each tasks
in the program.
Since SEDL programs have variables and CFSA do not,
it is the job of the deriver to encode the state of the program's
variables and their influence on program control flow into the
structure of the CFSA.
The deriver achieves this by applying a wide-range of program
analysis and transformation techniques
including:
procedure inlining, loop unrolling, constant propagation,
constant folding, and dead-code elimination.
These techniques are applied to each program task in isolation and
can yield very large CFSA for tasks that manipulate large amounts of data.
The INCA tools are written in LISP; the current implementation uses
Harlequin's LispWorks. For the rw21 system the following commands
yield the expanded CFSA for the four system tasks:
$ lispworks
LispWorks: The Common Lisp Programming Environment
...
CL-USER 4 > (load "inca.lisp")
; Loading text file inca.lisp
; Loading text file toolset.lisp
; Loading fasl file fe.afasl
; Loading fasl file ig.afasl
; Loading fasl file ilp.afasl
; Loading fasl file spin.afasl
; Loading fasl file smv.afasl
; Loading fasl file cplex.afasl
INCA 3.3 loaded. Type (help) for information.
USER 5 > (derive "rw21" :expose '("writeWork"))
Translation complete
Executing writer_1..reader_2.reader_1.read_write_control.....
Queries:
("derive" :OK 1.1)
The quoted basename, rw21, of the SEDL input file is given
as the first parameter to the derive command.
The command accepts several optional parameters including
the :expose and :compress options.
The :expose option accepts a list (i.e., the leading ' is important) of quoted names of procedures in the program. With this option the deriver models calls (returns) to those procedures using internal statements with symbols built from call_ (return_) and the procedure name. The names of the internal statements for our example are call_writework and return_writework. Reasoning about procedure calls and returns would not be possible without this feature since all procedure calls are inlined by the deriver. It is important to note that use of the :expose option does not automatically define event predicates for the new internal statements; those must be defined explicitly through the predicate definition mechanism.
The :compress nil option will cause the deriver to skip live variable analysis and a subsequent optimization that automatically sets dead variables to their initial values. This can sometimes be useful when using state predicates.
INCA can output the CFSA for each task built by the deriver, as well as other information related to the derivation process, with the booklet command.
USER 6 > (booklet :fsas t) Booklet written to file rw21.book :OK
Finally, the deriver reads the file with the given basename and a .query extension, if it exists. This is the file in which one should place predicate definitions to be incorporated into the CFSA.
A useful feature that is unrelated to the INCA tools is LISP's facility for timing any command. Passing the command as an argument to the time command will execute the argument and report timing information.
INCA provides commands to output Promela programs for use with the SPIN model checker and transition systems for use with the SMV model checker from the collection of derived CFSA; these commands are spin-input and smv-input, respectively. Model checker input languages differ in their syntax as well as the programming models they support. The approach of the INCA translators is slightly different for the two model checkers. For SPIN, each task CFSA is translated to a Promela process where shared labels in the CFSA are implemented with synchronous communication in Promela. For SMV, the transition relations of the individual CFSA are composed into the global transition relation which is expressed as a TRANS statement.
As mentioned earlier, an important feature of these tools is their ability to encode predicate definitions in the model checker input. The predicate definitions in the .query file serve as the default set of definitions. Users can override this default. For example, the predicates for a spin-input command can be set with a quoted list of (<id> <predicate>) pairs following the :predicates keyword:
(spin-input :predicates '(("name1" <predicate1>) ... ))
There are two mechanisms for encoding predicate definitions into model checker input. The mechanisms are referred to as defining and embedding predicates; the user control the mechanism that is used through use of the :define and :embed parameters to the input translator commands.
The distinction between these approaches can be characterized as follows. Defining a predicate amounts to identifying the set of global states at which the predicate evaluates to true; thus, a defined predicate is a disjunction of equality comparisons of the current state and the states in that set. Embedding a predicate actually modifies the CFSA by adding new system states that are used to model points at which the predicate will become true. This is done by introducing boolean state variables for each embedded predicate and transitions which set and unset it at appropriate places.
Embedding predicates will increase the size of the state space to be model checked, but it is not clear how it will affect the overall cost of analysis when compared to defined predicates. One should not embed unnecessary predicates for the property being verified--the fewer predicates embedded, the smaller the state space. Extra, unused, defined predicates appear to have no affect on performance. This means that users can have a single query file with all of the predicates for a system then selectively embed only those that are needed.
It is important to note that the semantics of the after event predicate is different if the predicate is embedded. An embedded event predicate (e.g., (after "A")) is true in global states where the event (e.g., "A") just occurred. This mean that the predicate is true for a single step of the transition system, unless the action is repeated. This eliminates the need for additional internal statements in the system that are there to insure that the state after an event is unique. Thus, one common strategy for predicate definition is to :embed event predicates and :define state predicates.
The input translator commands allow one to freely mix embedding and definition. For example, the smv-input command:
(smv-input :embed '("pred1" "pred2") :define '("pred3"))
embeds predicates pred1 and pred2 while still defining pred3;
these predicates would have been defined in the .query file.
The keyword :all is used to define or embed
all predicates listed
in the .query file. For example:
(smv-input :embed :all)The spin-input command takes the same parameters.
For the rw21 example we used the following commands:
USER 7 > (spin-input :embed '("callwriteWork" "callstopwrite"
"callstartwrite" "call_writeWork")
:define '("writerpresentfalse" "activereaders0"))
SPIN input written to file rw21.prom
NIL
USER 8 > (smv-input :embed '("callwriteWork" "callstopwrite"
"callstartwrite" "call_writeWork")
:define '("writerpresentfalse" "activereaders0"))
SMV input written to file rw21.trans
NIL
Writing temporal logic specifications for system requirements can be a challenge for a number of reasons, not the least of which is lack of familiarity with the formalisms (e.g., LTL and CTL) used by model checkers. We advocate an approach to writing specifications that involves the reuse of parameterized specification patterns. The approach is described in [DAC98b, DAC98a] and an extensive web-site has been developed to support its application at http://www.cis.ksu.edu/~dwyer/spec-patterns.html
The specifications for the rw21 example were written using the patterns. Note that the strings used to define predicates can be used as proposition names in LTL and CTL formula without modification.
SMV and SPIN are flexible tools with a large number of options and configuration parameters. We refer the reader to the the documentation for those tools which can be found at http://netlib.bell-labs.com/netlib/spin/whatispin.html for SPIN and http://www.cs.cmu.edu/~modelcheck for SMV.
Here we describe only the small portion of the model checker input files that is related to predicate definitions. The complete files are given for SPIN and SMV are rw21.prom and rw21.trans, respectively.
SPIN's input language, Promela, is C-like. Promela files can include the C pre-processor directives #include, to inline definitions in other files, and #define, to establish macro definitions. SMV's input language has no support for inlining portions of other files, but it does provide the DEFINE directive for establishing macro definitions. These directives are exploited in encoding predicates into model checker input.
For each defined predicate, the SPIN translator will output a #define to define the name of the predicate as a disjunction of Promela location predicates (name[pid]@label is true if the process with type name and id pid is currently executing at the statement following label). For each embedded predicate, the SPIN translator introduces a bit variable and appropriate transitions to set and reset it. Selected definitions for the rw21 example are illustrated in Figure 7.
Figure 6: Embedded and Defined Predicates for SPIN
The analogous definitions produced by the SMV translator are given in Figure 8.
Figure 7: Embedded and Defined Predicates for SMV
We note that for SMV, a predicate's boolean state variable is declared next to the state variable for the task that the predicate is associated with. For TRANS inputs SMV uses the order of variable declaration in the file as the variable order in the BDD, so the placement of the predicate state variables is important for performance.
The predicate names can be used directly in LTL formulae fed to the spin -f or in CTL formulae appended to the SMV transition system input.
The SPIN translator allows an additional option which will insert a directive for the model checker to incorporate the Büchi automaton for the LTL specification to be checked. For example, the command:
USER > (spin-input :never "prop4a")will cause the SPIN translator to add the line
#include "prop4a.never"at the bottom of the Promela file. If the :never parameter contains a '.', it will be used as-is (.never will not be appended). Note that checking deadlock is built into SPIN and requires no specification.
Unfortunately, the SMV input language does not support a #include-like directive. Currently, the .trans file are edited to append the CTL specification. A simple strategy for incorporating different CTL specifications into a transition system definition is to simply concatenate the files and submit them to SMV, e.g.:
$ cat sys.trans property.ctl | smv
Checking for deadlock with CTL requires a specification that is dependent on the final states of the CFSA. The smv-input command will automatically generate this specification when given the :spec :deadlock option.
One of the nice features of the predicate definition mechanism is that counter-examples for failed model checks are presented, e.g., by SMV, in terms of changes in the values of state variables and DEFINEd quantities. Since defined and embedded predicates use these mechanisms, this makes it very easy to interpret the counter-example in terms of the property and a source-level model of system behavior.
For example, the property:
AG(callstartwrite -> AF(callstartread1 | callstartread2))fails to hold on the rw21 system. SMV produces a counter-example that gives the changes in state variable and DEFINE values along a path through the system on which the property does not hold. Eliminating all information in the counter-example except the boolean variables for the embedded predicates and the DEFINEs for the defined predicates that appear in the property specification gives the counter-example in Figure 8.
Figure 8: Reduced SMV Counter-example
It is easy to see from this counter-example that the loop consists
solely of task rendezvous as a result of calls to the
Start_Write entries of the Read_Write_Control
task.
In other words, if the writer continually requests and is granted service
by the controller then the readers will never start.
Without predicate definitions interpretation of this counter-example
is significantly more complicated (e.g., one needs to compute
the set of predicates that are true in each state).
For embedded predicates, SPIN counter-examples provide essentially the same information as with SMV. Further work is required to provide similar support for defined predicates in SPIN.
There are several potential improvements that might be made to these tools.
We have described the capabilities and illustrated the usage of a toolset that supports a seven step methodology for model checking properties of an Ada program. Those steps are:
91
98b
95